Cara bootstrapping di r (dengan contoh)
Bootstrapping adalah metode yang dapat digunakan untuk memperkirakan kesalahan standar suatu statistik dan menghasilkan interval kepercayaan untuk statistik tersebut.
Proses dasar untuk bootstrap adalah sebagai berikut:
- Ambil k sampel replikasi dengan penggantian dari kumpulan data tertentu.
- Untuk setiap sampel, hitung statistik minat.
- Hal ini memberikan k perkiraan berbeda untuk statistik tertentu, yang kemudian dapat Anda gunakan untuk menghitung kesalahan standar statistik dan membuat interval kepercayaan untuk statistik tersebut.
Kita dapat melakukan bootstrap di R menggunakan fungsi berikut dari perpustakaan bootstrap :
1. Hasilkan sampel bootstrap.
boot(data, statistik, R,…)
Emas:
- data: vektor, matriks, atau blok data
- statistik: fungsi yang menghasilkan statistik yang akan dimulai
- A: Jumlah pengulangan bootstrap
2. Hasilkan interval kepercayaan bootstrap.
boot.ci(objek boot, conf, ketik)
Emas:
- bootobject: Objek yang dikembalikan oleh fungsi boot()
- conf : Interval kepercayaan yang akan dihitung. Nilai defaultnya adalah 0,95
- type : Jenis interval kepercayaan yang akan dihitung. Pilihannya mencakup ‘standar’, ‘basic’, ‘stud’, ‘perc’, ‘bca’ dan ‘all’ – defaultnya adalah ‘all’
Contoh berikut menunjukkan cara menggunakan fungsi-fungsi ini dalam praktik.
Contoh 1: bootstrap statistik tunggal
Kode berikut menunjukkan cara menghitung kesalahan standar untuk R-kuadrat dari model regresi linier sederhana:
set.seed(0) library (boot) #define function to calculate R-squared rsq_function <- function (formula, data, indices) { d <- data[indices,] #allows boot to select sample fit <- lm(formula, data=d) #fit regression model return (summary(fit)$r.square) #return R-squared of model } #perform bootstrapping with 2000 replications reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp) #view results of boostrapping reps ORDINARY NONPARAMETRIC BOOTSTRAP Call: boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ available) Bootstrap Statistics: original bias std. error t1* 0.7183433 0.002164339 0.06513426
Dari hasilnya kita dapat melihat:
- Estimasi R-squared untuk model regresi ini adalah 0.7183433 .
- Kesalahan standar untuk perkiraan ini adalah 0,06513426 .
Kami juga dapat dengan cepat memvisualisasikan distribusi sampel bootstrap:
plot(reps)
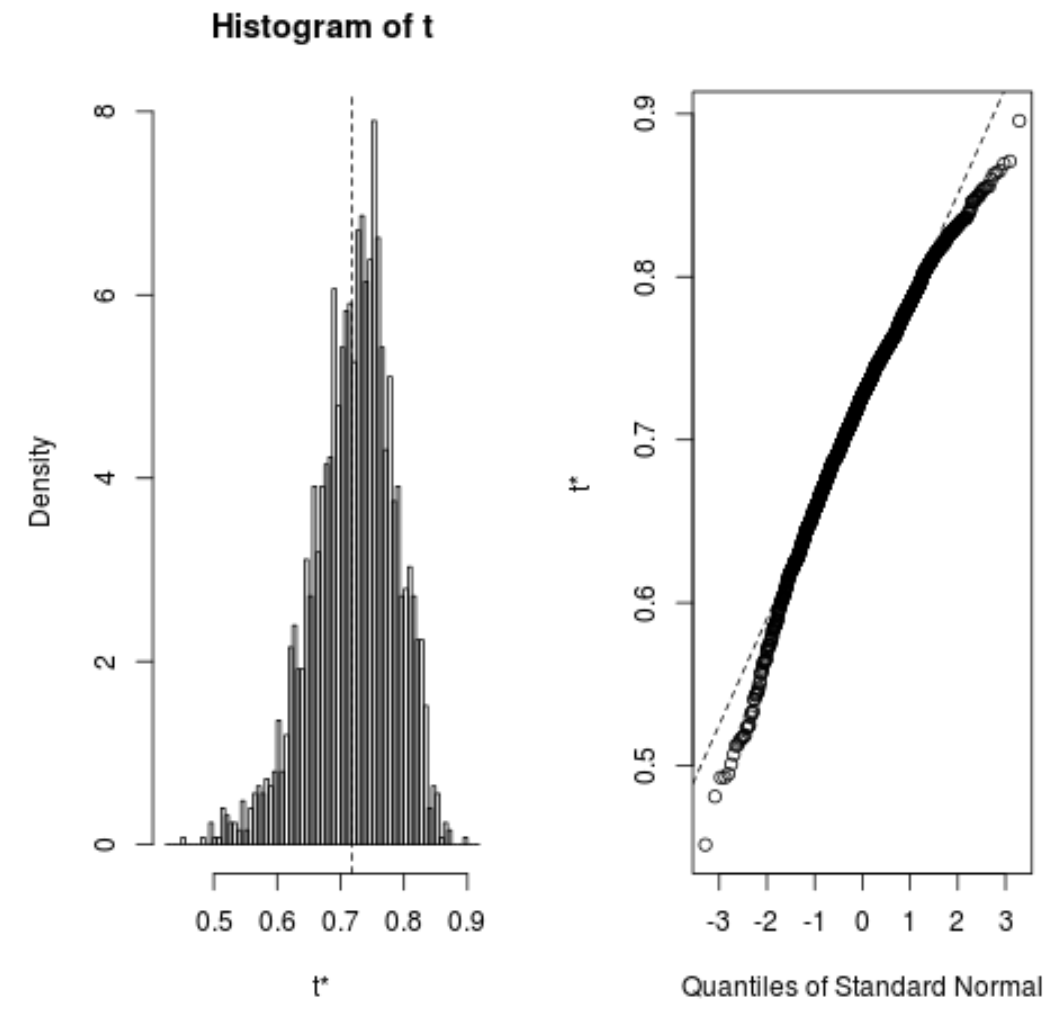
Kita juga dapat menggunakan kode berikut untuk menghitung interval kepercayaan 95% untuk estimasi R-kuadrat model:
#calculate adjusted bootstrap percentile (BCa) interval boot.ci(reps, type=" bca ") CALL: boot.ci(boot.out = reps, type = "bca") Intervals: Level BCa 95% (0.5350, 0.8188) Calculations and Intervals on Original Scale
Dari hasilnya terlihat bahwa interval kepercayaan 95% bootstrap untuk nilai R-kuadrat sebenarnya adalah (0,5350, 0,8188).
Contoh 2: bootstrap beberapa statistik
Kode berikut menunjukkan cara menghitung kesalahan standar untuk setiap koefisien dalam model regresi linier berganda:
set.seed(0) library (boot) #define function to calculate fitted regression coefficients coef_function <- function (formula, data, indices) { d <- data[indices,] #allows boot to select sample fit <- lm(formula, data=d) #fit regression model return (coef(fit)) #return coefficient estimates of model } #perform bootstrapping with 2000 replications reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp) #view results of boostrapping reps ORDINARY NONPARAMETRIC BOOTSTRAP Call: boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ available) Bootstrap Statistics: original bias std. error t1* 29.59985476 -5.058601e-02 1.49354577 t2* -0.04121512 6.549384e-05 0.00527082
Dari hasilnya kita dapat melihat:
- Koefisien perkiraan untuk intersep model adalah 29.59985476 dan kesalahan standar perkiraan ini adalah 1.49354577 .
- Koefisien estimasi disp variabel prediktor dalam model adalah -0.04121512 dan standar error estimasi ini adalah 0.00527082 .
Kami juga dapat dengan cepat memvisualisasikan distribusi sampel bootstrap:
plot(reps, index=1) #intercept of model plot(reps, index=2) #disp predictor variable
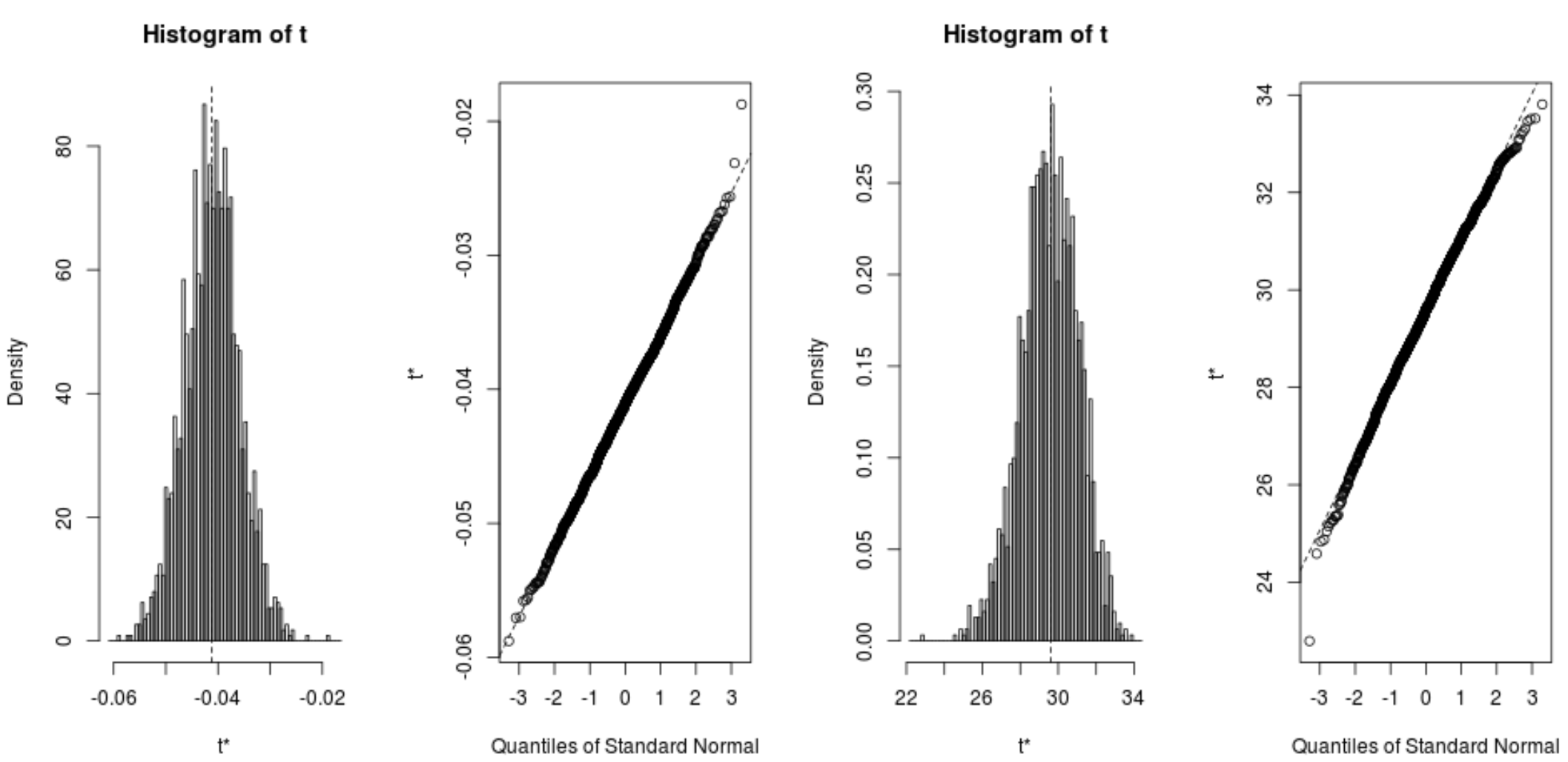
Kita juga dapat menggunakan kode berikut untuk menghitung interval kepercayaan 95% untuk setiap koefisien:
#calculate adjusted bootstrap percentile (BCa) intervals boot.ci(reps, type=" bca ", index=1) #intercept of model boot.ci(reps, type=" bca ", index=2) #disp predictor variable CALL: boot.ci(boot.out = reps, type = "bca", index = 1) Intervals: Level BCa 95% (26.78, 32.66) Calculations and Intervals on Original Scale BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS Based on 2000 bootstrap replicates CALL: boot.ci(boot.out = reps, type = "bca", index = 2) Intervals: Level BCa 95% (-0.0520, -0.0312) Calculations and Intervals on Original Scale
Dari hasil tersebut terlihat bahwa interval kepercayaan 95% bootstrap untuk koefisien model adalah sebagai berikut:
- IC untuk intersepsi: (26.78, 32.66)
- CI untuk tampilan : (-.0520, -.0312)
Sumber daya tambahan
Cara melakukan regresi linier sederhana di R
Cara melakukan regresi linier berganda di R
Pengantar Interval Keyakinan