Pengantar regresi ridge

Dalam regresi linier berganda biasa, kami menggunakan sekumpulan variabel prediktor p dan variabel respons agar sesuai dengan model dalam bentuk:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Emas:

• Y : Variabel respon
• X _j : variabel prediktif ^ke -j
• β _j : Efek rata-rata pada Y dari peningkatan satu unit X _j , dengan menganggap semua prediktor lainnya tetap
• ε : Istilah kesalahan

Nilai β ₀ , β ₁ , B ₂ , …, β _p dipilih menggunakan metode kuadrat terkecil , yang meminimalkan jumlah kuadrat residu (RSS):

RSS = Σ(y _saya – ŷ _saya ) ²

Emas:

• Σ : Simbol Yunani yang berarti jumlah
• y _i : nilai respon sebenarnya untuk observasi ^ke-i
• ŷ _i : Nilai respons yang diprediksi berdasarkan model regresi linier berganda

Namun, ketika variabel prediktor berkorelasi tinggi, multikolinearitas bisa menjadi masalah. Hal ini dapat membuat estimasi koefisien model tidak dapat diandalkan dan menunjukkan varians yang tinggi.

Salah satu cara untuk mengatasi masalah ini tanpa menghilangkan sepenuhnya variabel prediktor tertentu dari model adalah dengan menggunakan metode yang dikenal sebagai regresi ridge , yang berupaya meminimalkan hal-hal berikut:

RSS + λΣβ _j ²

dimana j beralih dari 1 ke p dan λ ≥ 0.

Suku kedua dalam persamaan ini dikenal sebagai penalti penarikan .

Ketika λ = 0, suku penalti ini tidak berpengaruh dan regresi ridge menghasilkan estimasi koefisien yang sama dengan kuadrat terkecil. Namun, ketika λ mendekati tak terhingga, penalti penyusutan menjadi lebih berpengaruh dan perkiraan koefisien regresi puncak mendekati nol.

Secara umum, variabel prediktor yang paling kecil pengaruhnya dalam model akan menurun paling cepat menuju nol.

Mengapa menggunakan Regresi Ridge?

Keuntungan regresi Ridge dibandingkan regresi kuadrat terkecil adalah tradeoff bias-varians .

Ingatlah bahwa Mean Square Error (MSE) adalah metrik yang dapat kita gunakan untuk mengukur keakuratan model tertentu dan dihitung sebagai berikut:

MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE = Varians + Bias ² + Kesalahan yang tidak dapat direduksi

Ide dasar regresi Ridge adalah untuk memperkenalkan bias kecil sehingga varians dapat dikurangi secara signifikan, sehingga menghasilkan UMK yang lebih rendah secara keseluruhan.

Untuk mengilustrasikannya, perhatikan grafik berikut:

Perhatikan bahwa ketika λ meningkat, variansnya berkurang secara signifikan dengan peningkatan bias yang sangat kecil. Namun, setelah melewati titik tertentu, varians berkurang dengan lebih cepat dan penurunan koefisien menyebabkan perkiraan yang terlalu rendah, sehingga menyebabkan peningkatan tajam dalam bias.

Kita dapat melihat dari grafik bahwa MSE pengujian paling rendah ketika kita memilih nilai λ yang menghasilkan trade-off optimal antara bias dan varians.

Ketika λ = 0, suku penalti dalam regresi ridge tidak berpengaruh dan oleh karena itu menghasilkan estimasi koefisien yang sama dengan kuadrat terkecil. Namun, dengan meningkatkan λ hingga titik tertentu, kita dapat mengurangi MSE pengujian secara keseluruhan.

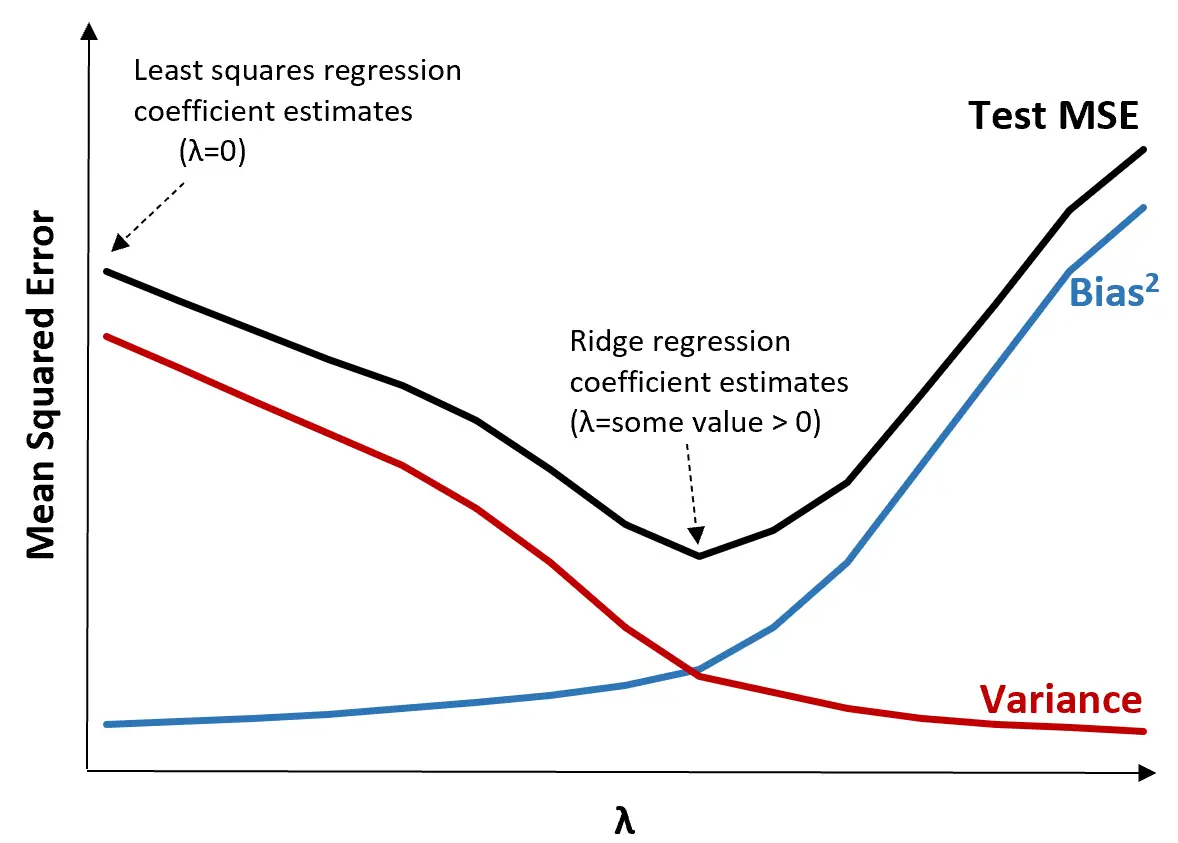
Artinya, fitting model dengan regresi ridge akan menghasilkan error pengujian yang lebih kecil dibandingkan dengan fitting model dengan regresi kuadrat terkecil.

Langkah-Langkah Melakukan Regresi Ridge dalam Praktek

Langkah-langkah berikut dapat digunakan untuk melakukan regresi ridge:

Langkah 1: Hitung matriks korelasi dan nilai VIF untuk variabel prediktor.

Pertama, kita perlu membuat matriks korelasi dan menghitung nilai VIF (variance inflasi faktor) untuk setiap variabel prediktor.

Jika kita mendeteksi korelasi yang kuat antara variabel prediktor dan nilai VIF yang tinggi (beberapa teks mendefinisikan nilai VIF “tinggi” sebagai 5 sementara yang lain menggunakan 10), maka regresi ridge mungkin tepat.

Namun, jika tidak terdapat multikolinearitas pada data, regresi ridge mungkin tidak perlu dilakukan terlebih dahulu. Sebagai gantinya, kita dapat melakukan regresi kuadrat terkecil biasa.

Langkah 2: Standarisasi setiap variabel prediktor.

Sebelum melakukan regresi ridge, kita perlu menskalakan data sedemikian rupa sehingga setiap variabel prediktor memiliki rata-rata 0 dan standar deviasi 1. Hal ini memastikan bahwa tidak ada satu variabel prediktor yang memiliki pengaruh berlebihan saat menjalankan regresi ridge.

Langkah 3: Sesuaikan model regresi ridge dan pilih nilai λ.

Tidak ada rumus pasti yang dapat kita gunakan untuk menentukan nilai apa yang akan digunakan untuk λ. Dalam praktiknya, ada dua cara umum untuk memilih λ:

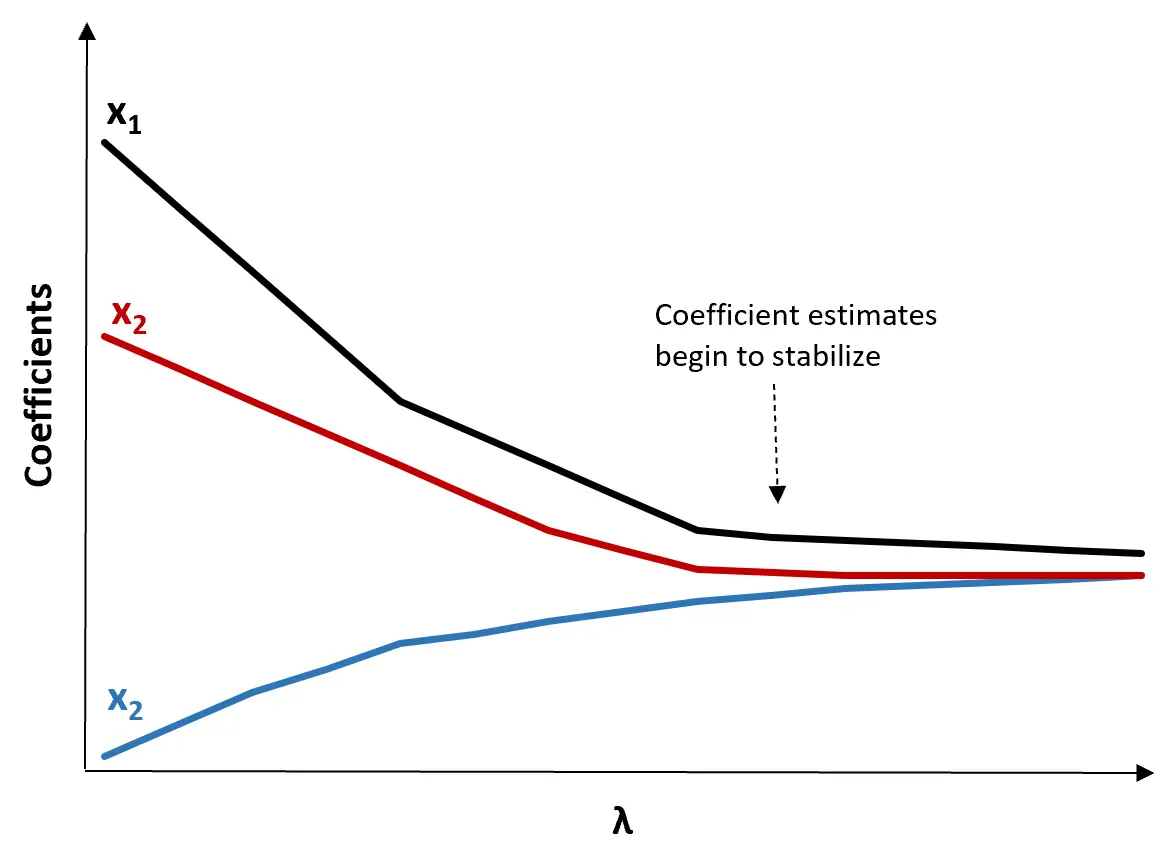
(1) Buat plot jejak Ridge. Ini adalah grafik yang memvisualisasikan nilai perkiraan koefisien seiring dengan peningkatan λ menuju tak terhingga. Biasanya, kita memilih λ sebagai nilai dimana sebagian besar estimasi koefisien mulai stabil.

(2) Hitung uji MSE untuk setiap nilai λ.

Cara lain untuk memilih λ adalah dengan menghitung MSE pengujian setiap model dengan nilai λ yang berbeda dan memilih λ sebagai nilai yang menghasilkan MSE pengujian terendah.

Keuntungan dan Kerugian Regresi Ridge

Keuntungan terbesar dari regresi Ridge adalah kemampuannya untuk menghasilkan test mean square error (MSE) yang lebih rendah daripada kuadrat terkecil ketika terdapat multikolinearitas.

Namun, kelemahan terbesar dari regresi Ridge adalah ketidakmampuannya melakukan pemilihan variabel karena mencakup semua variabel prediktor dalam model akhir. Karena beberapa prediktor akan berkurang mendekati nol, hal ini dapat mempersulit interpretasi hasil model.

Dalam praktiknya, regresi Ridge berpotensi menghasilkan model yang mampu membuat prediksi lebih baik dibandingkan model kuadrat terkecil, namun seringkali lebih sulit untuk menginterpretasikan hasil model.

Bergantung pada apakah interpretasi model atau akurasi perkiraan lebih penting bagi Anda, Anda dapat memilih untuk menggunakan regresi kuadrat terkecil atau regresi ridge dalam skenario yang berbeda.

Regresi Ridge dalam R & Python

Tutorial berikut menjelaskan cara melakukan regresi ridge di R dan Python, dua bahasa yang paling umum digunakan untuk menyesuaikan model regresi ridge:

Regresi Ridge di R (langkah demi langkah)
Regresi Ridge dengan Python (Langkah demi Langkah)