Regresi lasso di r (langkah demi langkah)

Regresi laso adalah metode yang dapat kita gunakan untuk menyesuaikan model regresi ketika terdapat multikolinearitas dalam data.

Singkatnya, regresi kuadrat terkecil berupaya menemukan estimasi koefisien yang meminimalkan jumlah sisa kuadrat (RSS):

RSS = Σ(y _saya – ŷ _saya )2

Emas:

• Σ : Simbol Yunani yang berarti jumlah
• y _i : nilai respon sebenarnya untuk observasi ^ke-i
• ŷ _i : Nilai respons yang diprediksi berdasarkan model regresi linier berganda

Sebaliknya, regresi laso berupaya meminimalkan hal-hal berikut:

RSS + λΣ|β _j |

dimana j beralih dari 1 ke p variabel prediktor dan λ ≥ 0.

Suku kedua dalam persamaan ini dikenal sebagai penalti penarikan . Dalam regresi laso, kami memilih nilai λ yang menghasilkan uji MSE (mean square error) serendah mungkin.

Tutorial ini memberikan contoh langkah demi langkah tentang cara melakukan regresi laso di R.

Langkah 1: Muat data

Untuk contoh ini, kita akan menggunakan kumpulan data bawaan R yang disebut mtcars . Kita akan menggunakan hp sebagai variabel respon dan variabel berikut sebagai prediktor:

• mpg
• berat
• kotoran
• qdetik

Untuk melakukan regresi laso, kita akan menggunakan fungsi dari paket glmnet . Paket ini mengharuskan variabel respon berupa vektor dan himpunan variabel prediktor berasal dari kelas data.matrix .

Kode berikut menunjukkan cara mendefinisikan data kita:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

Langkah 2: Sesuaikan Model Regresi Lasso

Selanjutnya, kita akan menggunakan fungsi glmnet() agar sesuai dengan model regresi laso dan menentukan alpha=1 .

Perhatikan bahwa menetapkan alpha sama dengan 0 setara dengan menggunakan regresi ridge dan mengatur alpha ke nilai antara 0 dan 1 setara dengan menggunakan jaring elastis.  

Untuk menentukan nilai mana yang akan digunakan untuk lambda, kami akan melakukan k-fold cross-validation dan mengidentifikasi nilai lambda yang menghasilkan test mean squared error (MSE) terendah.

Perhatikan bahwa fungsi cv.glmnet() secara otomatis melakukan validasi silang k-fold menggunakan k = 10 kali.

 library (glmnet)

#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 5.616345

#produce plot of test MSE by lambda value
plot(cv_model) 

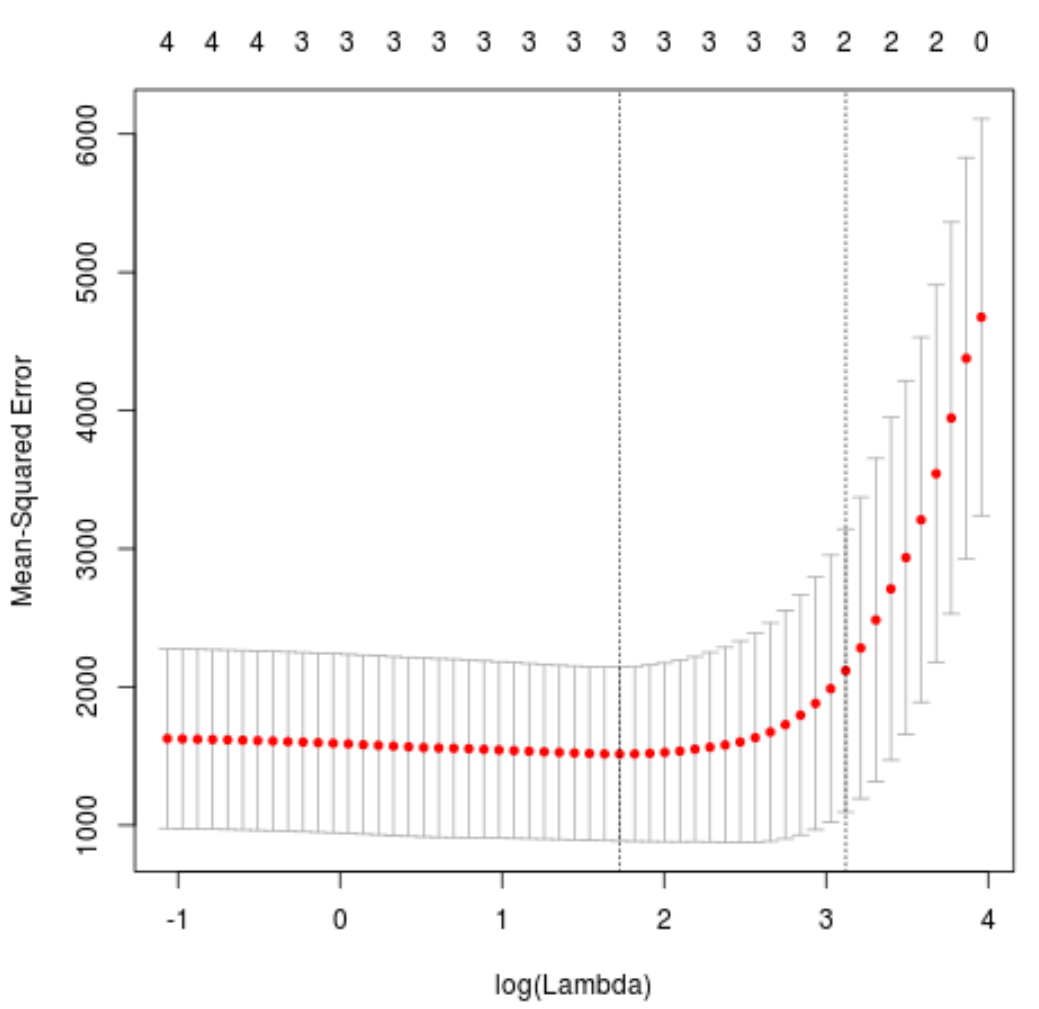
Nilai lambda yang meminimalkan uji MSE ternyata adalah 5.616345 .

Langkah 3: Analisis model akhir

Terakhir, kita dapat menganalisis model akhir yang dihasilkan dengan nilai lambda optimal.

Kita dapat menggunakan kode berikut untuk mendapatkan estimasi koefisien untuk model ini:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                   s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.      
qsec -19.43425

Tidak ada koefisien yang ditampilkan untuk prediktor drat karena regresi laso mengurangi koefisien menjadi nol. Ini berarti dia dikeluarkan sepenuhnya dari model karena dia tidak memiliki pengaruh yang cukup.

Perhatikan bahwa ini adalah perbedaan utama antara regresi ridge dan regresi laso . Regresi ridge mengurangi semua koefisien menuju nol, namun regresi laso berpotensi menghilangkan prediktor dari model dengan mengurangi koefisien sepenuhnya menjadi nol.

Kita juga dapat menggunakan model regresi laso final untuk membuat prediksi tentang observasi baru. Misalnya kita mempunyai mobil baru dengan atribut berikut:

• mpg: 24
• berat: 2,5
• harga: 3,5
• qdetik: 18.5

Kode berikut menunjukkan cara menggunakan model regresi laso yang dipasang untuk memprediksi nilai hp dari pengamatan baru ini:

 #define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 ) 

#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)

[1,] 109.0842

Berdasarkan nilai yang dimasukkan, model memperkirakan mobil ini akan memiliki nilai hp sebesar 109.0842 .

Terakhir, kita dapat menghitung R-kuadrat model pada data pelatihan:

 #use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.8047064

R kuadratnya ternyata 0,8047064 . Artinya, model terbaik mampu menjelaskan 80,47% variasi nilai respon data latih.

Anda dapat menemukan kode R lengkap yang digunakan dalam contoh ini di sini .