Pengantar regresi polinomial
Saat kita memiliki kumpulan data dengan variabel prediktor dan variabel respons , kita sering menggunakan regresi linier sederhana untuk mengukur hubungan antara kedua variabel.
Namun, regresi linier sederhana (SLR) mengasumsikan bahwa hubungan antara prediktor dan variabel respon adalah linier. Ditulis dalam notasi matematika, SLR mengasumsikan hubungan tersebut berbentuk:
Y = β 0 + β 1 X + ε
Namun dalam praktiknya, hubungan antara kedua variabel mungkin bersifat nonlinier dan upaya menggunakan regresi linier dapat menghasilkan model yang tidak sesuai.
Salah satu cara untuk memperhitungkan hubungan nonlinier antara variabel prediktor dan respons adalah dengan menggunakan regresi polinomial , yang berbentuk:
Y = β 0 + β 1 X + β 2 X 2 + … + β h
Dalam persamaan ini, h disebut derajat polinomial.
Saat kita meningkatkan nilai h , model akan mampu mengakomodasi hubungan nonlinier dengan lebih baik, namun dalam praktiknya kita jarang memilih h yang lebih besar dari 3 atau 4. Di luar titik ini, model menjadi terlalu fleksibel dan terlalu cocok dengan data .
Catatan teknis
- Meskipun regresi polinomial dapat memuat data nonlinier, namun tetap dianggap sebagai bentuk regresi linier karena koefisiennya linier β1 , β2 , …, βh .
- Regresi polinomial juga dapat digunakan untuk beberapa variabel prediktor, namun hal ini menciptakan istilah interaksi dalam model, yang dapat membuat model menjadi sangat kompleks jika beberapa variabel prediktor digunakan.
Kapan menggunakan regresi polinomial
Kami menggunakan regresi polinomial ketika hubungan antara prediktor dan variabel respons bersifat nonlinier.
Ada tiga cara umum untuk mendeteksi hubungan nonlinier:
1. Buat diagram sebar.
Cara paling sederhana untuk mendeteksi hubungan nonlinier adalah dengan membuat plot sebar antara variabel respons versus variabel prediktor.
Misalnya, jika kita membuat diagram sebar berikut, kita dapat melihat bahwa hubungan antara kedua variabel kira-kira linier, sehingga regresi linier sederhana mungkin dapat berfungsi dengan baik pada data ini.
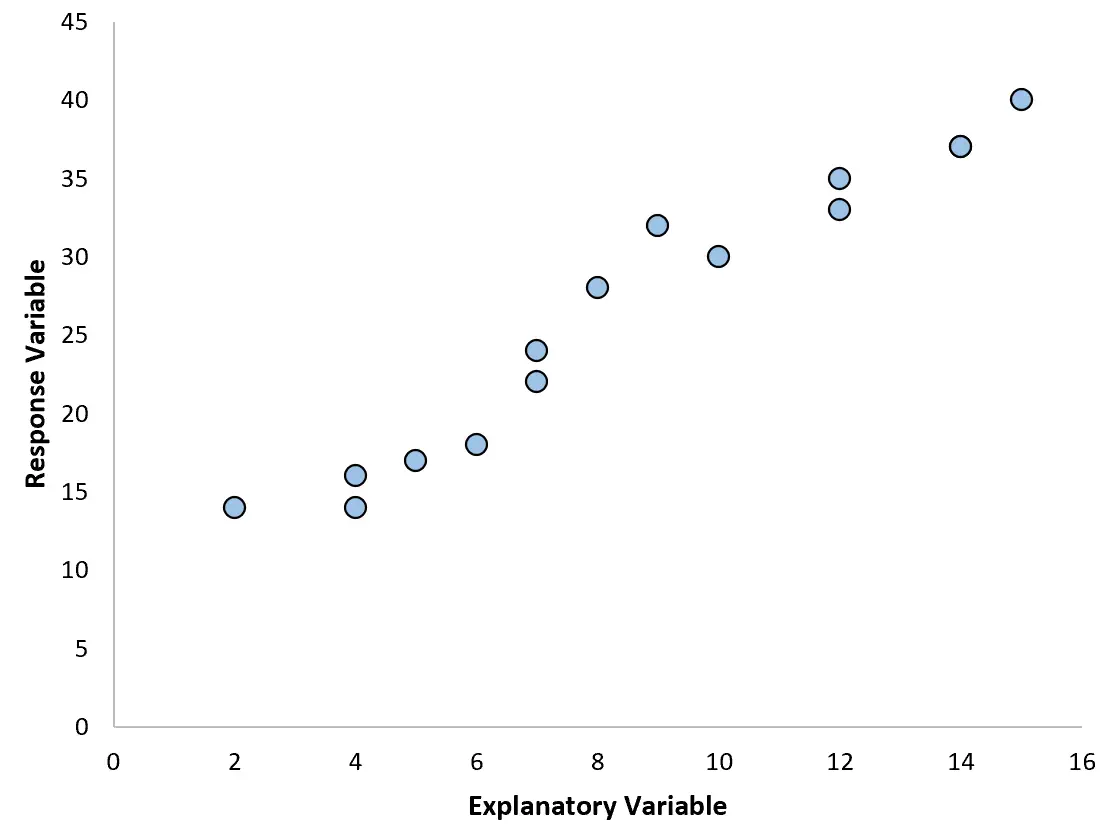
Namun, jika plot sebar kita terlihat seperti salah satu grafik berikut, kita mungkin melihat bahwa hubungannya tidak linier dan oleh karena itu regresi polinomial merupakan ide yang bagus:
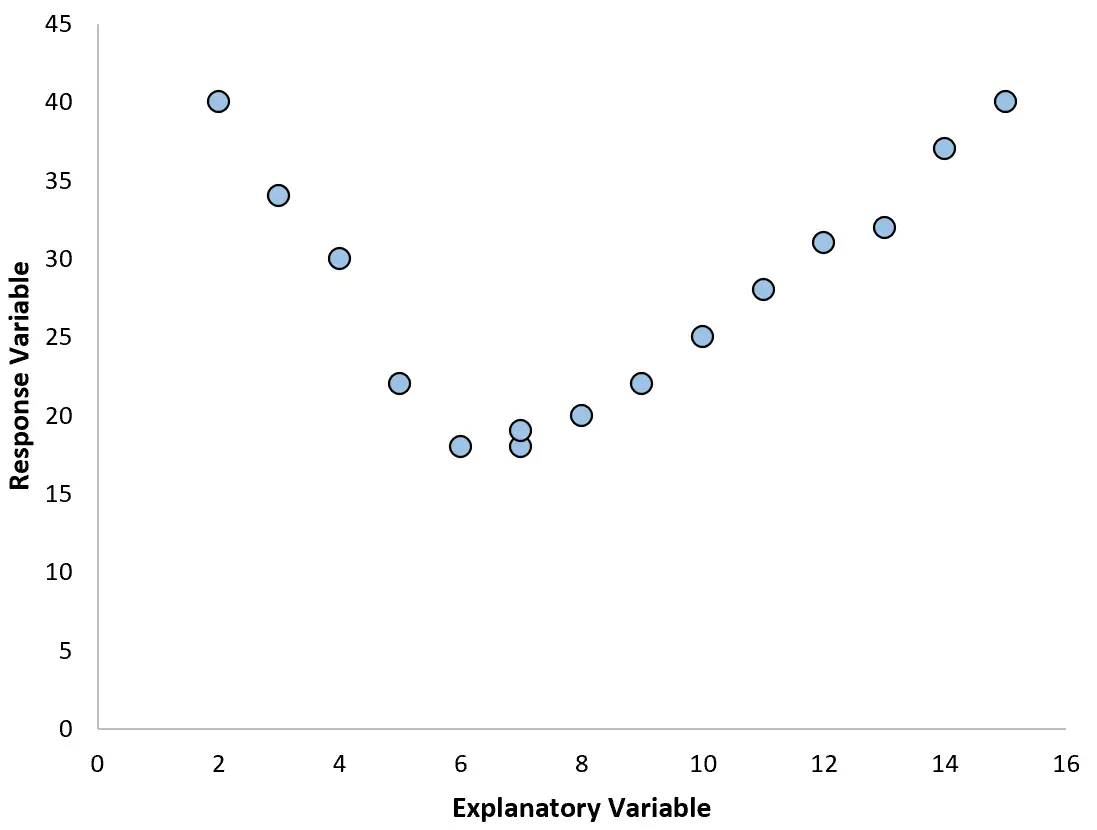
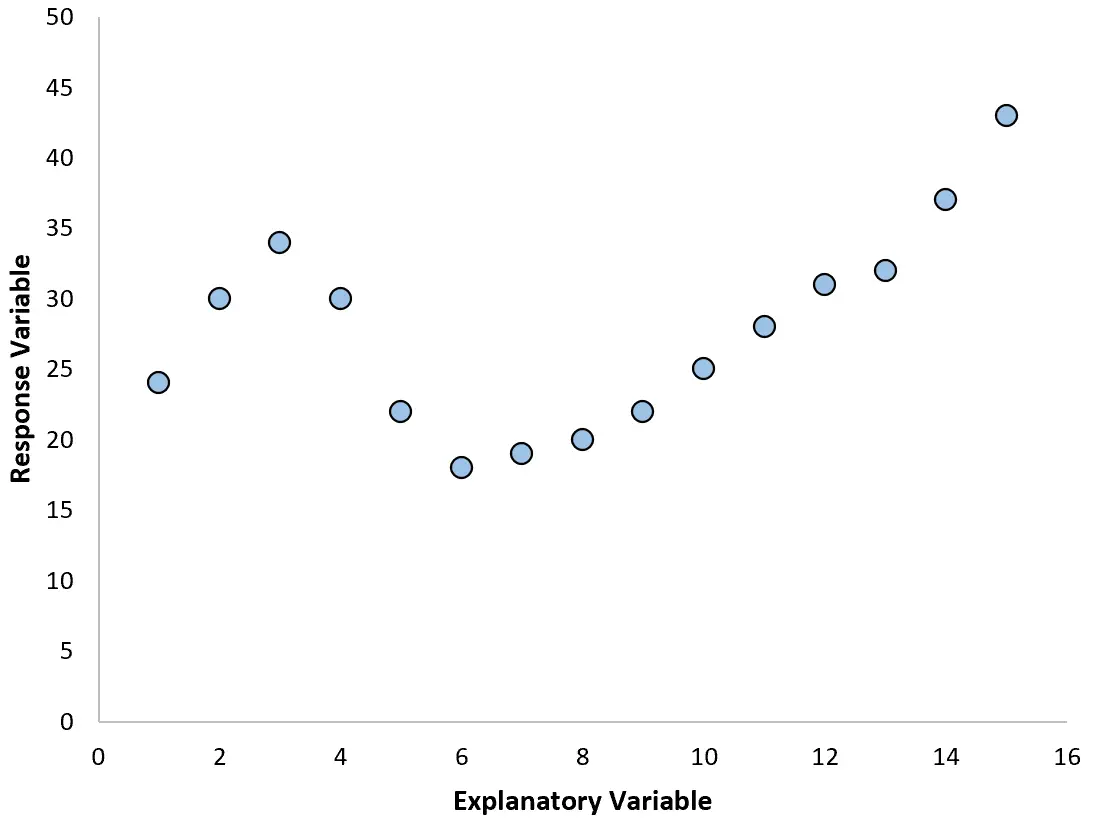
2. Buatlah plot residu terhadap plot yang dipasang.
Cara lain untuk mendeteksi nonlinier adalah dengan menyesuaikan model regresi linier sederhana dengan data dan kemudian membuat plot residu terhadap nilai yang dipasang .
Jika sisa plot didistribusikan secara merata di sekitar nol tanpa tren yang jelas, maka regresi linier sederhana mungkin sudah cukup.
Namun, jika residu menunjukkan tren nonlinier pada grafik, hal ini menunjukkan bahwa hubungan antara prediktor dan respons kemungkinan besar nonlinier.
3. Hitung R 2 model.
Nilai R 2 model regresi menunjukkan persentase variasi variabel respons yang dapat dijelaskan oleh variabel prediktor.
Jika Anda memasukkan model regresi linier sederhana ke kumpulan data dan nilai R2 model tersebut cukup rendah, hal ini dapat menunjukkan bahwa hubungan antara prediktor dan variabel respons lebih kompleks daripada hubungan linier sederhana.
Ini mungkin merupakan tanda bahwa Anda mungkin perlu mencoba regresi polinomial.
Terkait: Berapa nilai R-kuadrat yang bagus?
Bagaimana memilih derajat polinomial
Model regresi polinomial mengambil bentuk berikut:
Y = β 0 + β 1 X + β 2 X 2 + … + β h
Dalam persamaan ini, h adalah derajat polinomial.
Tapi bagaimana cara memilih nilai h ?
Dalam praktiknya, kami menyesuaikan beberapa model berbeda dengan nilai h yang berbeda dan melakukan validasi silang k-fold untuk menentukan model mana yang menghasilkan mean squared error (MSE) pengujian terendah.
Misalnya, kita dapat menyesuaikan model berikut ke kumpulan data tertentu:
- kamu = β 0 + β 1
- Y = β 0 + β 1 X + β 2 X 2
- Y = β0 + β1X + β2X2 + β3X3
- Y = β 0 + β 1 X + β 2 X 2 + β 3 X 3 + β 4 X 4
Kita kemudian dapat menggunakan validasi silang k-fold untuk menghitung pengujian MSE untuk setiap model, yang akan memberi tahu kita seberapa baik kinerja setiap model pada data yang belum pernah dilihat sebelumnya.
Pengorbanan bias-varians dari regresi polinomial
Ada tradeoff bias-varians saat menggunakan regresi polinomial. Saat kita meningkatkan derajat polinomial, biasnya berkurang (karena model menjadi lebih fleksibel) tetapi variansnya meningkat.
Seperti semua model pembelajaran mesin, kita perlu menemukan keseimbangan optimal antara bias dan varians.
Dalam sebagian besar kasus, hal ini memungkinkan derajat polinomial ditingkatkan hingga batas tertentu, namun melampaui nilai tertentu, model mulai beradaptasi dengan gangguan dalam data dan MSE pengujian mulai menurun.
Untuk memastikan bahwa kami cocok dengan model yang fleksibel namun tidak terlalu fleksibel, kami menggunakan validasi silang k-fold untuk menemukan model yang menghasilkan pengujian MSE terendah.
Cara melakukan regresi polinomial
Tutorial berikut memberikan contoh cara melakukan regresi polinomial di berbagai perangkat lunak:
Cara Melakukan Regresi Polinomial di Excel
Bagaimana melakukan regresi polinomial di R
Cara melakukan regresi polinomial dengan Python
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya