Spline regresi adaptif multivariat di r
Spline regresi adaptif multivariat (MARS) dapat digunakan untuk memodelkan hubungan nonlinier antara sekumpulan variabel prediktor dan variabel respons .
Metode ini berfungsi sebagai berikut:
1. Bagilah kumpulan data menjadi k bagian.
2. Sesuaikan model regresi untuk setiap bagian.
3. Gunakan validasi silang k-fold untuk memilih nilai k .
Tutorial ini memberikan contoh langkah demi langkah tentang cara menyesuaikan model MARS ke kumpulan data di R.
Langkah 1: Muat paket yang diperlukan
Untuk contoh ini, kita akan menggunakan dataset ISLR Wage . paket yang berisi gaji tahunan 3.000 orang beserta berbagai variabel prediktor seperti usia, pendidikan, ras, dan lainnya.
Sebelum memasang model MARS ke data, kami akan memuat paket yang diperlukan:
library (ISLR) #contains Wage dataset library (dplyr) #data wrangling library (ggplot2) #plotting library (earth) #fitting MARS models library (caret) #tuning model parameters
Langkah 2: Lihat data
Selanjutnya, kami akan menampilkan enam baris pertama dari dataset yang sedang kami kerjakan:
#view first six rows of data
head (Wage)
year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574
Langkah 3: Buat dan optimalkan model MARS
Selanjutnya, kita akan membuat model MARS untuk kumpulan data ini dan melakukan validasi silang k-fold untuk menentukan model mana yang menghasilkan tes RMSE (mean square error) terendah.
#create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
nprune = seq (2, 50, length.out = 10) %>%
floor ())
#make this example reproducible
set.seed(1)
#fit MARS model using k-fold cross-validation
cv_mars <- train(
x = subset(Wage, select = -c(wage, logwage)),
y = Wage$wage,
method = " earth ",
metric = " RMSE ",
trControl = trainControl(method = " cv ", number = 10),
tuneGrid = hyper_grid)
#display model with lowest test RMSE
cv_mars$results %>%
filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554
Dari hasil tersebut, kita dapat melihat bahwa model yang menghasilkan MSE pengujian terendah adalah model yang hanya memiliki efek orde pertama (yaitu, tanpa suku interaksi) dan 12 suku. Model ini menghasilkan root mean square error (RMSE) sebesar 33.8164 .
Catatan: Kami menggunakan metode=”earth” untuk menentukan model MARS. Anda dapat menemukan dokumentasi untuk metode ini di sini .
Kita juga dapat membuat bagan untuk memvisualisasikan pengujian RMSE berdasarkan derajat dan jumlah suku:
#display test RMSE by terms and degree
ggplot(cv_mars)
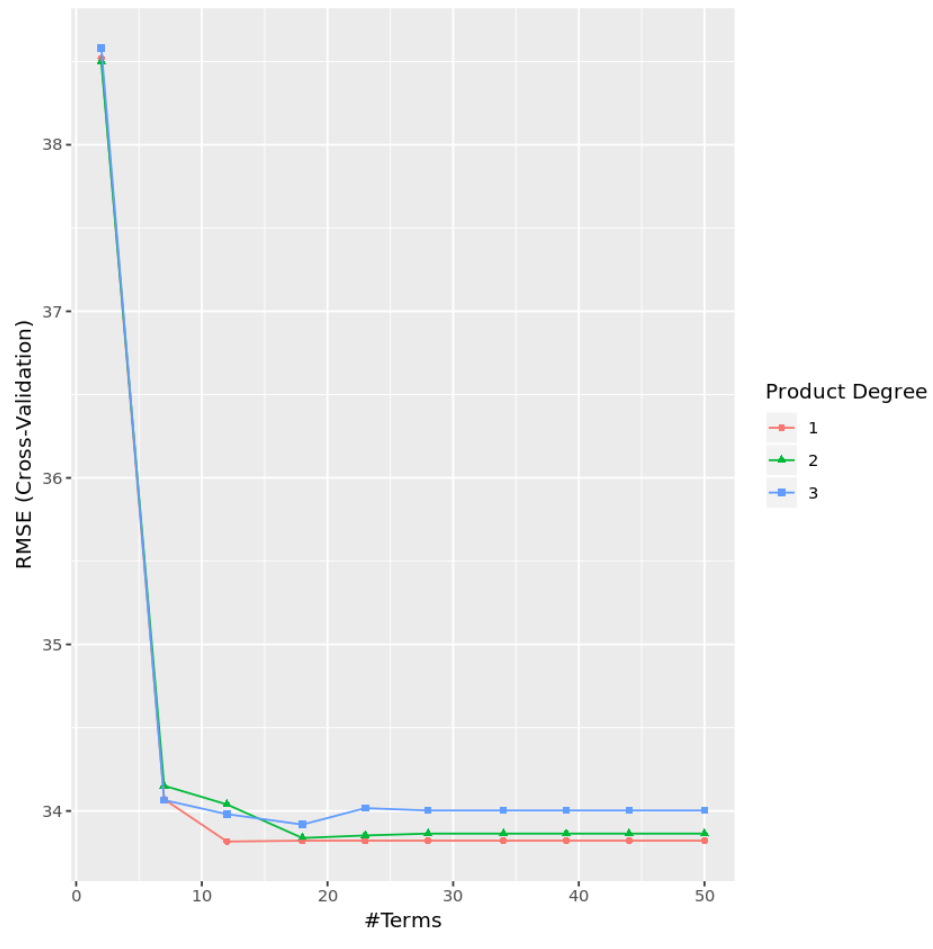
Dalam praktiknya, kami akan mengadaptasi model MARS dengan beberapa jenis model lain seperti:
- Regresi linier berganda
- Regresi polinomial
- Regresi puncak
- Regresi laso
- Regresi komponen utama
- Kuadrat terkecil parsial
Kami kemudian akan membandingkan setiap model untuk menentukan mana yang menghasilkan kesalahan pengujian terendah dan memilih model tersebut sebagai model optimal untuk digunakan.
Kode R lengkap yang digunakan dalam contoh ini dapat ditemukan di sini .