Cara menghitung distribusi sampling di r
Distribusi sampling adalah distribusi probabilitas suatu statistik tertentu berdasarkan banyak sampel acak dari satu populasi.
Tutorial ini menjelaskan cara melakukan hal berikut dengan distribusi sampling di R:
- Hasilkan distribusi pengambilan sampel.
- Visualisasikan distribusi pengambilan sampel.
- Hitung mean dan deviasi standar distribusi sampling.
- Hitung probabilitas mengenai distribusi sampling.
Hasilkan distribusi sampling di R
Kode berikut menunjukkan cara menghasilkan distribusi sampling di R:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656
Dalam contoh ini, kami menggunakan fungsi rnorm() untuk menghitung rata-rata 10.000 sampel yang masing-masing ukuran sampelnya adalah 20 dan dihasilkan dari distribusi normal dengan mean 5,3 dan standar deviasi 9.
Terlihat sampel pertama mempunyai mean 5,283992, sampel kedua mempunyai mean 6,304845, dan seterusnya.
Visualisasikan distribusi pengambilan sampel
Kode berikut menunjukkan cara membuat histogram sederhana untuk memvisualisasikan distribusi sampling:
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
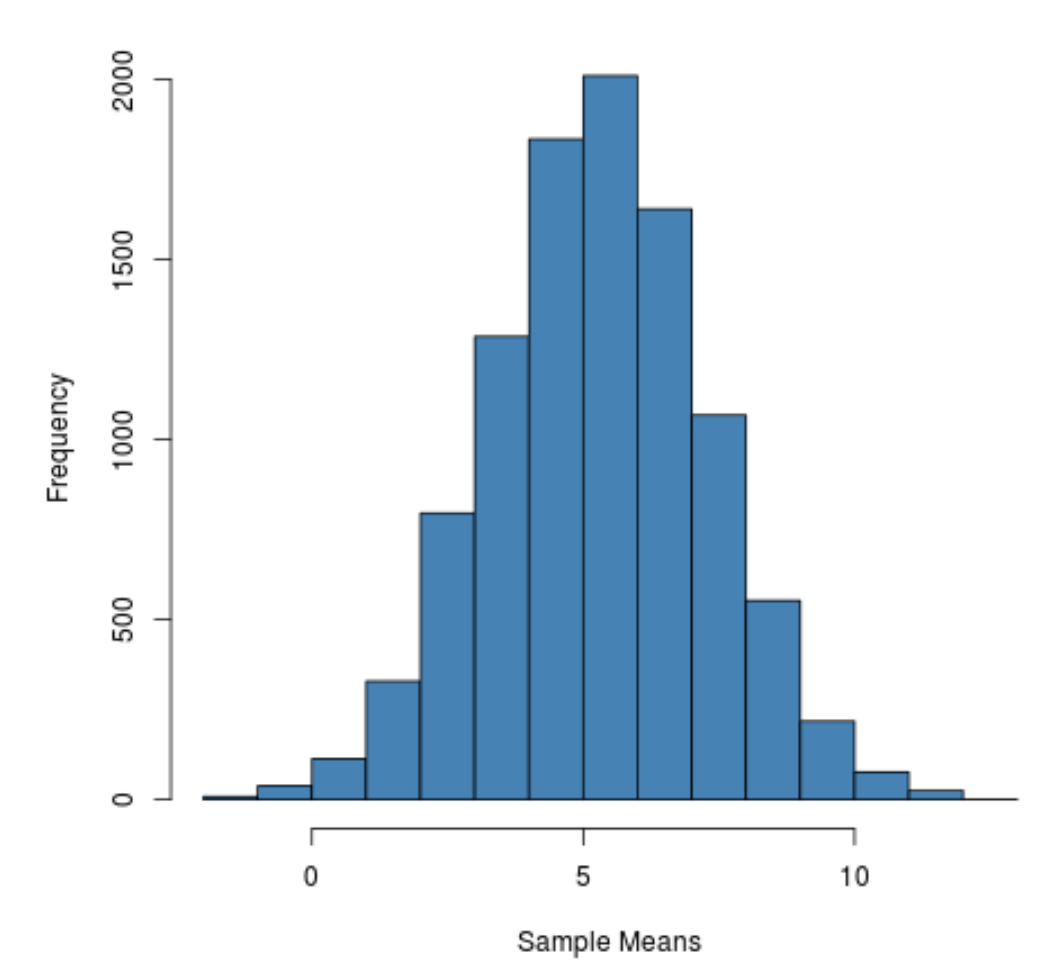
Terlihat distribusi samplingnya berbentuk lonceng dengan puncak mendekati nilai 5.
Namun dari ekor distribusinya kita dapat melihat bahwa beberapa sampel memiliki mean lebih besar dari 10 dan sampel lainnya memiliki mean kurang dari 0.
Temukan mean dan deviasi standar
Kode berikut menunjukkan cara menghitung mean dan deviasi standar distribusi sampling:
#mean of sampling distribution
mean(sample_means)
[1] 5.287195
#standard deviation of sampling distribution
sd(sample_means)
[1] 2.00224
Secara teoritis, rata-rata distribusi sampling harusnya 5,3. Kita dapat melihat bahwa mean sampel sebenarnya dalam contoh ini adalah 5.287195 , yang mendekati 5.3.
Dan secara teori, simpangan baku distribusi sampling harus sama dengan s/√n, yaitu 9 / √20 = 2,012. Kita dapat melihat bahwa simpangan baku aktual dari distribusi sampling adalah 2,00224 , yang mendekati 2,012.
Hitung probabilitasnya
Kode berikut menunjukkan cara menghitung probabilitas memperoleh nilai tertentu untuk mean sampel, dengan mempertimbangkan mean populasi, deviasi standar populasi, dan ukuran sampel.
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
Dalam contoh khusus ini, kita menemukan probabilitas bahwa mean sampel kurang dari atau sama dengan 6, mengingat mean populasi adalah 5,3, deviasi standar populasi adalah 9, dan ukuran sampel 20 adalah 0,6417 .
Ini sangat dekat dengan probabilitas yang dihitung oleh Kalkulator Distribusi Sampling :

Kode lengkap
Kode R lengkap yang digunakan dalam contoh ini ditunjukkan di bawah ini:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
#mean of sampling distribution
mean(sample_means)
#standard deviation of sampling distribution
sd(sample_means)
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
Sumber daya tambahan
Pengantar Distribusi Sampling
Kalkulator Distribusi Sampling
Pengantar Teorema Limit Pusat