Cara menghitung sisa siswa dengan python
Sisa siswa hanyalah sisa dibagi dengan perkiraan deviasi standarnya.
Dalam praktiknya, secara umum kita mengatakan bahwa observasi apa pun dalam kumpulan data yang sisa siswanya lebih besar dari nilai absolut 3 adalah outlier.
Kita dapat dengan cepat memperoleh sisa model regresi yang dipelajari dengan Python menggunakan fungsi OLSResults.outlier_test() dari statsmodels, yang menggunakan sintaks berikut:
Hasil OLS.outlier_test()
di mana OLSResults adalah nama kecocokan model linier menggunakan fungsi statsmodels ols() .
Contoh: perhitungan residu yang dipelajari dengan Python
Misalkan kita membangun model regresi linier sederhana berikut dengan Python:
#import necessary packages and functions import numpy as np import pandas as pd import statsmodels. api as sm from statsmodels. formula . api import ols #create dataset df = pd. DataFrame ({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86], 'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19]}) #fit simple linear regression model model = ols('rating ~ points', data=df). fit ()
Kita dapat menggunakan fungsi outlier_test() untuk menghasilkan DataFrame yang berisi sisa siswa untuk setiap observasi dalam kumpulan data:
#calculate studentized residuals stud_res = model. outlier_test () #display studentized residuals print(stud_res) student_resid unadj_p bonf(p) 0 -0.486471 0.641494 1.000000 1 -0.491937 0.637814 1.000000 2 0.172006 0.868300 1.000000 3 1.287711 0.238781 1.000000 4 0.106923 0.917850 1.000000 5 0.748842 0.478355 1.000000 6 -0.968124 0.365234 1.000000 7 -2.409911 0.046780 0.467801 8 1.688046 0.135258 1.000000 9 -0.014163 0.989095 1.000000
DataFrame ini menampilkan nilai berikut untuk setiap observasi dalam kumpulan data:
- Residu yang dipelajari
- Nilai p yang belum disesuaikan dari sisa siswa
- Nilai p sisa siswa yang dikoreksi Bonferroni
Terlihat bahwa sisa siswa pada observasi pertama pada dataset adalah -0.486471 , sisa siswa pada observasi kedua adalah -0.491937 , dan seterusnya.
Kita juga dapat membuat plot cepat dari nilai variabel prediktor terhadap sisa siswa yang sesuai:
import matplotlib. pyplot as plt #define predictor variable values and studentized residuals x = df[' points '] y = stud_res[' student_resid '] #create scatterplot of predictor variable vs. studentized residuals plt. scatter (x,y) plt. axhline (y=0, color=' black ', linestyle=' -- ') plt. xlabel (' Points ') plt. ylabel (' Studentized Residuals ')
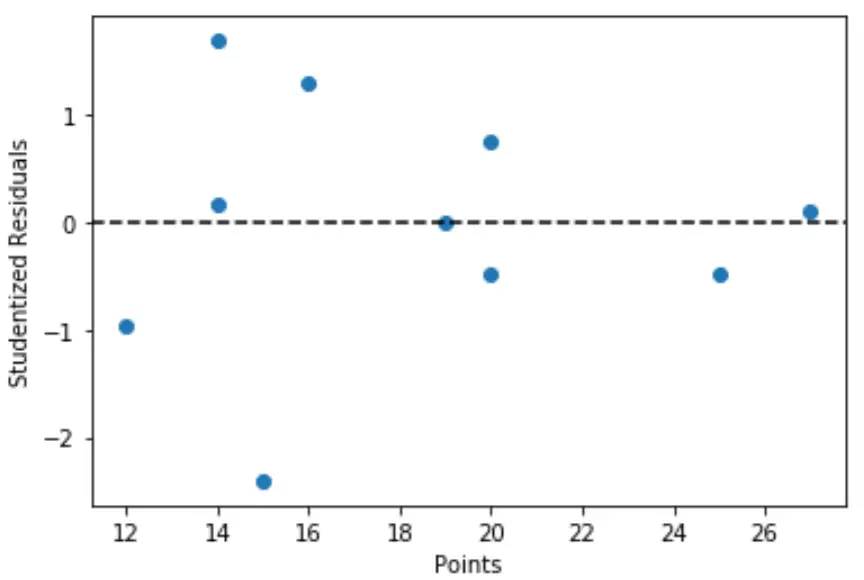
Dari grafik terlihat bahwa tidak ada satupun observasi yang memiliki sisa siswa dengan nilai absolut lebih besar dari 3, sehingga tidak ada outlier yang jelas pada dataset.
Sumber daya tambahan
Cara melakukan regresi linier sederhana dengan Python
Cara melakukan regresi linier berganda dengan Python
Cara Membuat Plot Sisa dengan Python