Cara melakukan transformasi box-cox dengan python
Transformasi box-cox adalah metode yang umum digunakan untuk mengubah kumpulan data yang tidak terdistribusi normal menjadi kumpulan data yang lebih terdistribusi normal .
Ide dasar di balik metode ini adalah mencari nilai λ sedemikian rupa sehingga data yang ditransformasikan sedekat mungkin dengan distribusi normal, dengan menggunakan rumus berikut:
- y(λ) = (y λ – 1) / λ jika y ≠ 0
- y(λ) = log(y) jika y = 0
Kita dapat melakukan transformasi box-cox dengan Python menggunakan fungsi scipy.stats.boxcox() .
Contoh berikut menunjukkan cara menggunakan fungsi ini dalam praktiknya.
Contoh: Transformasi Box-Cox dengan Python
Misalkan kita menghasilkan himpunan acak berisi 1000 nilai dari distribusi eksponensial :
#load necessary packages import numpy as np from scipy. stats import boxcox import seaborn as sns #make this example reproducible n.p. random . seeds (0) #generate dataset data = np. random . exponential (size= 1000 ) #plot the distribution of data values sns. distplot (data, hist= False , kde= True )
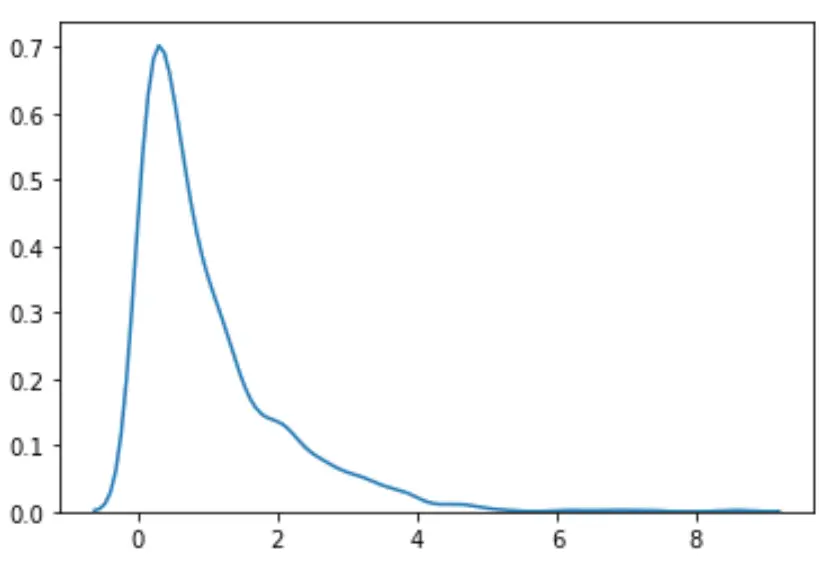
Terlihat distribusinya tidak normal.
Kita dapat menggunakan fungsi boxcox() untuk mencari nilai lambda optimal yang menghasilkan distribusi lebih normal:
#perform Box-Cox transformation on original data transformed_data, best_lambda = boxcox(data) #plot the distribution of the transformed data values sns. distplot (transformed_data, hist= False , kde= True )
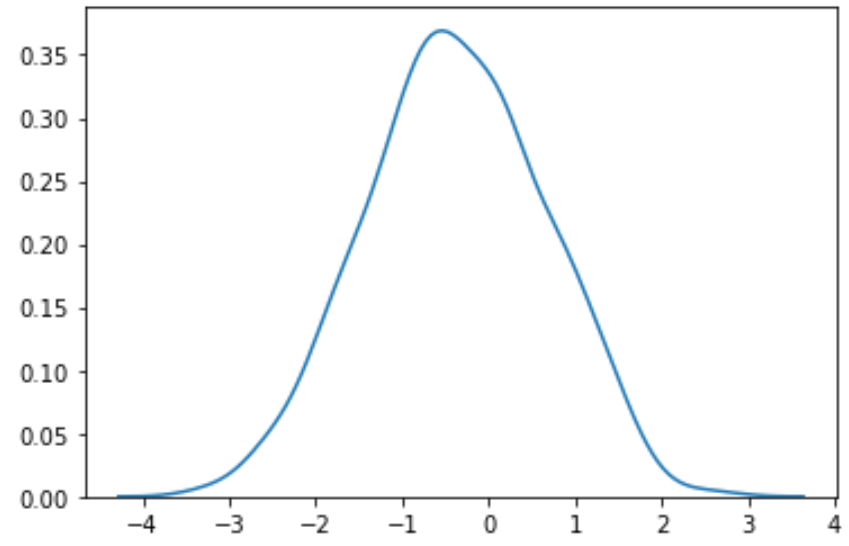
Kita dapat melihat bahwa data yang diubah mengikuti distribusi yang jauh lebih normal.
Kita juga dapat menemukan nilai lambda persis yang digunakan untuk melakukan transformasi Box-Cox:
#display optimal lambda value print (best_lambda) 0.2420131978174143
Lambda optimal ditemukan sekitar 0,242 .
Jadi, setiap nilai data ditransformasikan menggunakan persamaan berikut:
Baru = (lama 0,242 – 1) / 0,242
Kita dapat memastikannya dengan melihat nilai data asli versus data yang diubah:
#view first five values of original dataset data[0:5] array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849]) #view first five values of transformed dataset transformed_data[0:5] array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])
Nilai pertama dalam kumpulan data asli adalah 0.79587 . Jadi, kami menerapkan rumus berikut untuk mengubah nilai ini:
Baru = (.79587 0.242 – 1) / 0.242 = -0.222
Kami dapat mengonfirmasi bahwa nilai pertama dalam kumpulan data yang diubah memang -0.222 .
Sumber daya tambahan
Cara Membuat dan Menafsirkan Plot QQ dengan Python
Cara Melakukan Uji Normalitas Shapiro-Wilk dengan Python