Apa yang dimaksud dengan pembatasan ruang lingkup?

Seringkali dalam statistik kita berusaha mengukur korelasi antara dua variabel. Ini membantu kita memahami hal-hal berikut:

• Arah hubungan antara dua variabel. Ketika salah satu variabel meningkat, apakah variabel lainnya cenderung meningkat atau menurun?
• Kekuatan hubungan antara dua variabel. Berapa perubahan nilai kedua variabel tersebut?

Sayangnya, masalah yang mungkin timbul saat mengukur korelasi antara dua variabel disebut pembatasan rentang . Hal ini terjadi ketika rentang nilai terukur untuk salah satu variabel dibatasi karena alasan tertentu.

Misalnya kita ingin mengukur korelasi antara jam belajar dengan nilai ujian siswa di sekolah tertentu.

Jika kita mengumpulkan data mengenai kedua variabel ini untuk seluruh 1.000 siswa di sekolah, kita mungkin menemukan bahwa korelasi antara jam belajar dan nilai ujian adalah 0,73 .

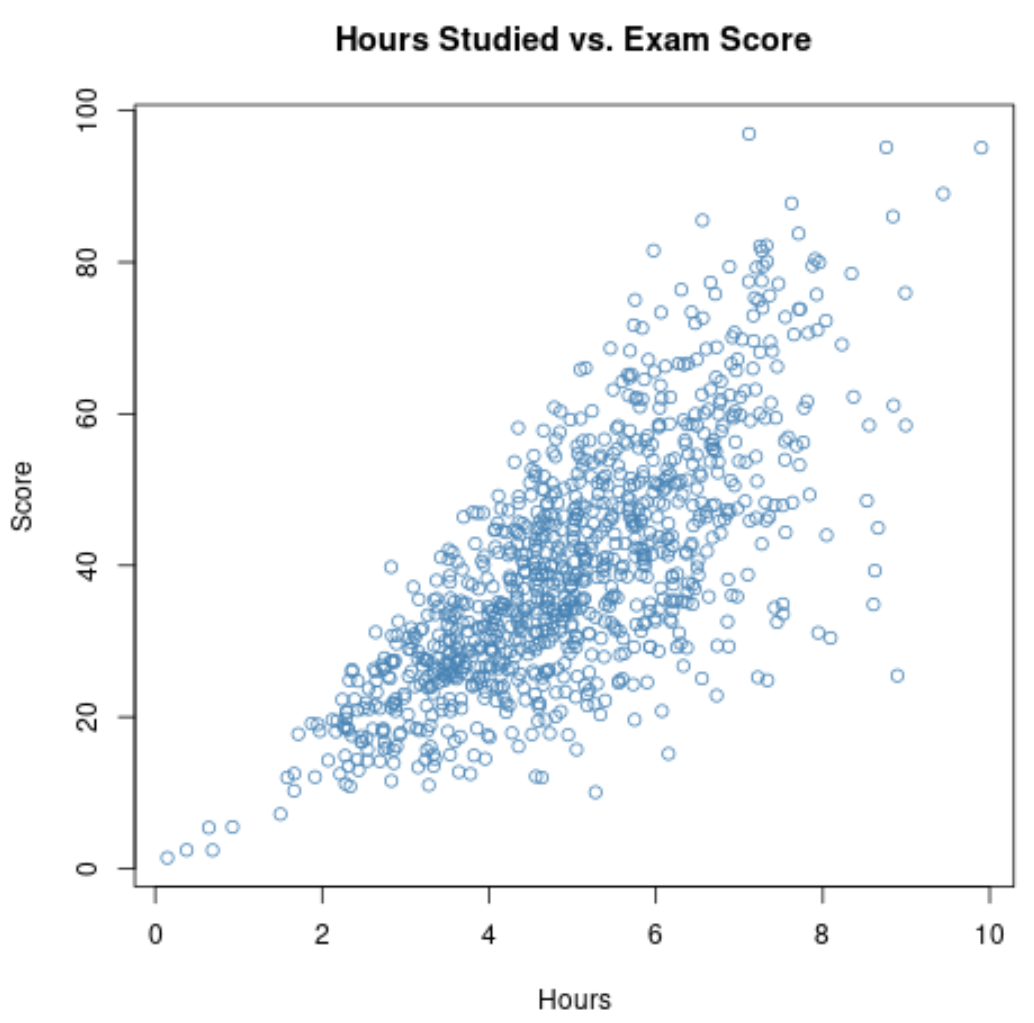
Korelasi yang cukup tinggi menunjukkan adanya hubungan positif yang kuat antara kedua variabel. Ketika siswa belajar lebih banyak, mereka cenderung berprestasi lebih baik dalam ujian.

Namun, mari kita asumsikan bahwa kita hanya mengumpulkan data siswa pada mata kuliah kehormatan. Bisa jadi semua siswa tersebut sudah belajar minimal 6 jam.

Jadi, jika kita menghitung korelasi antara jam belajar dan nilai ujian siswa tersebut, kita akan menggunakan kisaran sempit untuk variabel jam belajar .

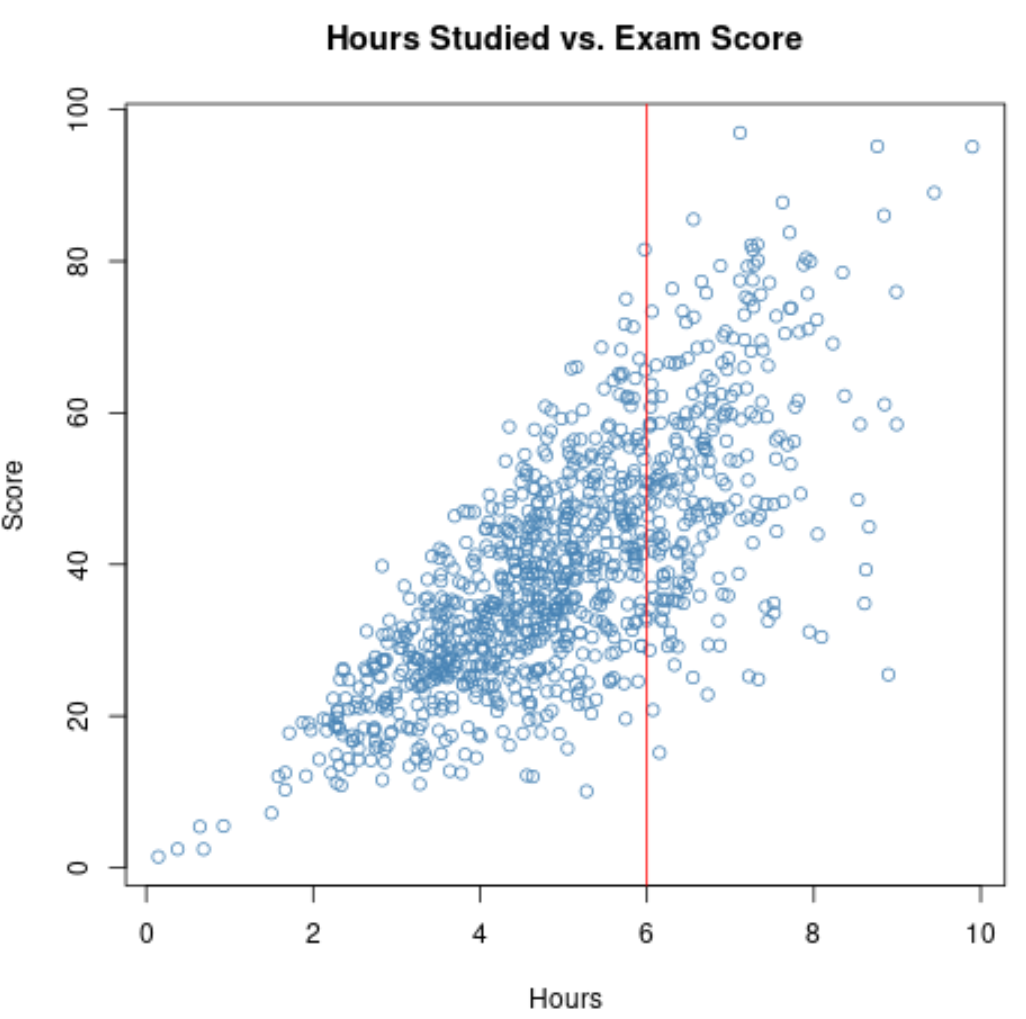
Jika kita memperbesar diagram sebar untuk rentang yang jamnya lebih besar dari 6, maka plotnya akan terlihat seperti ini:

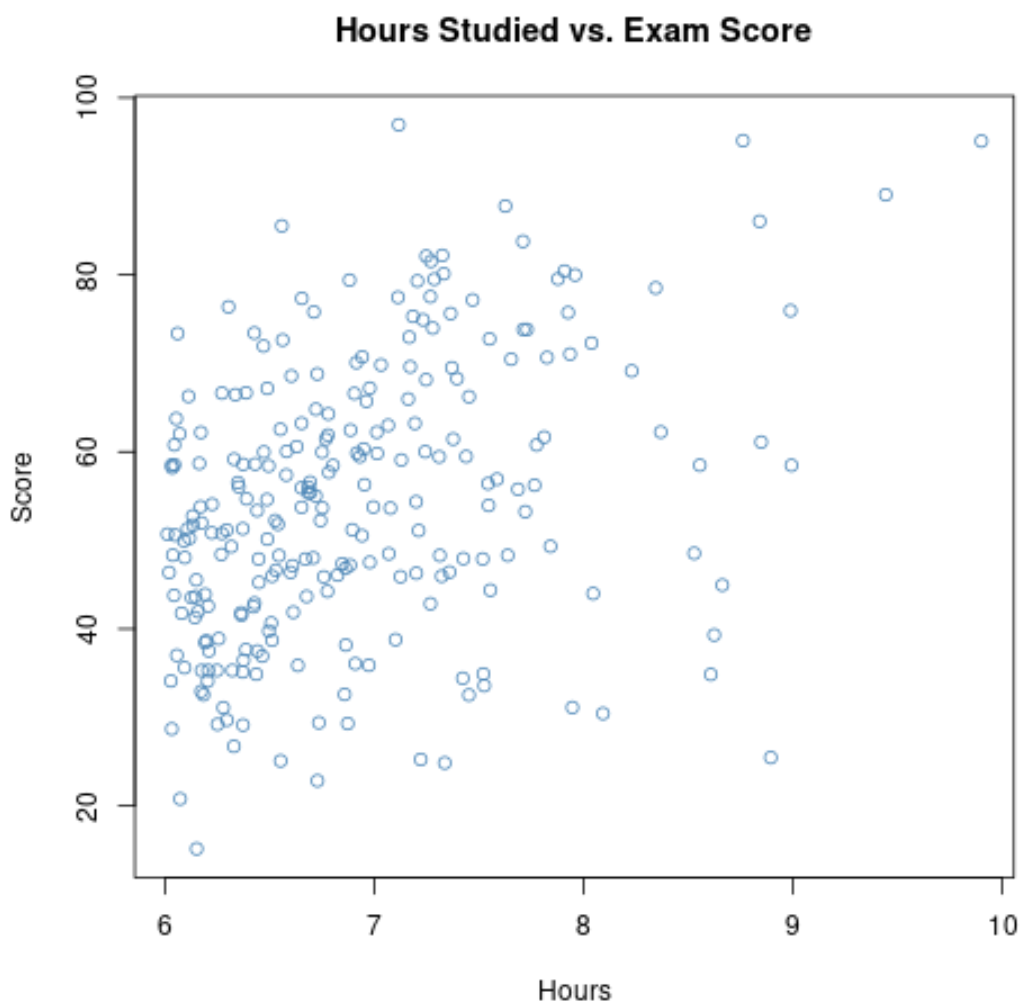
Korelasi antara kedua variabel pada grafik ini ternyata sebesar 0,37 , jauh lebih rendah dari 0,73 .

Jadi, jika kita hanya mengumpulkan data tentang jam belajar dan nilai ujian untuk siswa pada mata kuliah kehormatan, kita mungkin berasumsi bahwa ada hubungan yang lemah antara jam belajar dan nilai ujian.

Namun, hasil ini akan menyesatkan karena kami menggunakan rentang terbatas untuk salah satu variabel.

Contoh nyata dari jangkauan terbatas

Masalah rentang terbatas dapat muncul dalam praktik di banyak penelitian berbeda. Berikut beberapa contohnya:

1. Studi pada atlet berprestasi . Para peneliti mungkin tertarik untuk mempelajari apakah program pelatihan tertentu menghasilkan lebih banyak massa otot daripada program standar tertentu.

Jika peneliti hanya mengumpulkan data dari atlet elit, kemungkinan besar atlet tersebut semuanya sudah memiliki massa otot yang tinggi. Oleh karena itu, akan ada rentang nilai sempit yang tersedia untuk menghitung korelasi antara program pelatihan dan massa otot yang dihasilkan.

2. Kajian terhadap siswa yang berprestasi. Peneliti mungkin ingin mempelajari apakah program bimbingan belajar tertentu mempunyai dampak positif terhadap nilai. Secara alami, siswa yang ingin meningkatkan nilainya dan berpartisipasi dalam program bimbingan belajar mungkin sudah menjadi siswa yang berprestasi.

Jadi mungkin tidak banyak ruang untuk perbaikan pada nilai siswa ini. Ketika peneliti menghitung korelasi antara jam yang dihabiskan dalam program bimbingan belajar dan peningkatan nilai yang dihasilkan, korelasi sebenarnya mungkin diremehkan karena ruang untuk peningkatan nilai terbatas.

Bagaimana memperhitungkan rentang yang dibatasi

Cara populer untuk memperhitungkan rentang terbatas dikenal sebagai Kasus Thorndike 2 , sebuah rumus yang dikembangkan oleh ahli psikometri Robert L. Thorndike.

Rumus ini memberikan perkiraan korelasi sebenarnya antara dua variabel dan menggunakan perhitungan berikut:

Korelasi sebenarnya = √(1-(SD ² _{y dibatasi} -SD ² _{y tidak dibatasi} )) * (1-r ² _dibatasi )

Emas:

• SD ² _{dibatasi y} : Standar deviasi kuadrat dari data yang tersedia pada variabel respon y.
• SD ² y _{yang tidak dibatasi} : Standar deviasi kuadrat yang diketahui dari variabel respons populasi.
• r ² _dibatasi : Korelasi kuadrat pada data terbatas yang tersedia.

Rumus ini telah terbukti efektif dalam menghasilkan perkiraan yang tidak bias mengenai korelasi sebenarnya antara dua variabel ketika salah satu variabel mempunyai rentang yang terbatas.

Perhatikan bahwa untuk menggunakan rumus ini, Anda harus memiliki perkiraan deviasi standar populasi sebenarnya untuk variabel respons.