Tes brown – forsythe di r: contoh langkah demi langkah

ANOVA satu arah digunakan untuk menentukan ada atau tidaknya perbedaan yang signifikan antara rata-rata tiga atau lebih kelompok independen.

Salah satu asumsi ANOVA satu arah adalah varian populasi yang diambil sampelnya adalah sama.

Salah satu cara paling umum untuk mengujinya adalah dengan menggunakan uji Brown-Forsythe , yaitu uji statistik yang menggunakan asumsi berikut:

• H ₀ : Varians antar populasi adalah sama.
• H _A : Perbedaan antar populasi tidak sama.

Jika nilai p dari uji tersebut berada di bawah tingkat signifikansi tertentu (misalnya α = 0,05), maka kita menolak hipotesis nol dan menyimpulkan bahwa variansnya tidak sama antara populasi yang berbeda.

Tutorial ini memberikan contoh langkah demi langkah tentang cara melakukan tes Brown-Forsythe di R.

Langkah 1: Masukkan datanya

Misalkan kita ingin mengetahui apakah tiga program latihan yang berbeda menghasilkan tingkat penurunan berat badan yang berbeda atau tidak.

Untuk mengujinya, kami merekrut 90 orang dan secara acak menugaskan 30 orang untuk menggunakan setiap program. Kami kemudian mengukur penurunan berat badan setiap orang setelah satu bulan.

Kumpulan data berikut berisi informasi tentang jumlah penurunan berat badan pada setiap program:

 #make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)),
                   weight_loss = c( runif (30, 0, 3),
                                   runif (30, 0, 5),
                                   runif (30, 1, 7)))

#view first six rows of data frame
head(data)

# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458

Langkah 2: Ringkas dan visualisasikan data

Sebelum melakukan tes Brown-Forsythe, kita dapat membuat plot kotak untuk memvisualisasikan varian penurunan berat badan untuk setiap kelompok:

 boxplot(weight_loss ~ program, data = data)

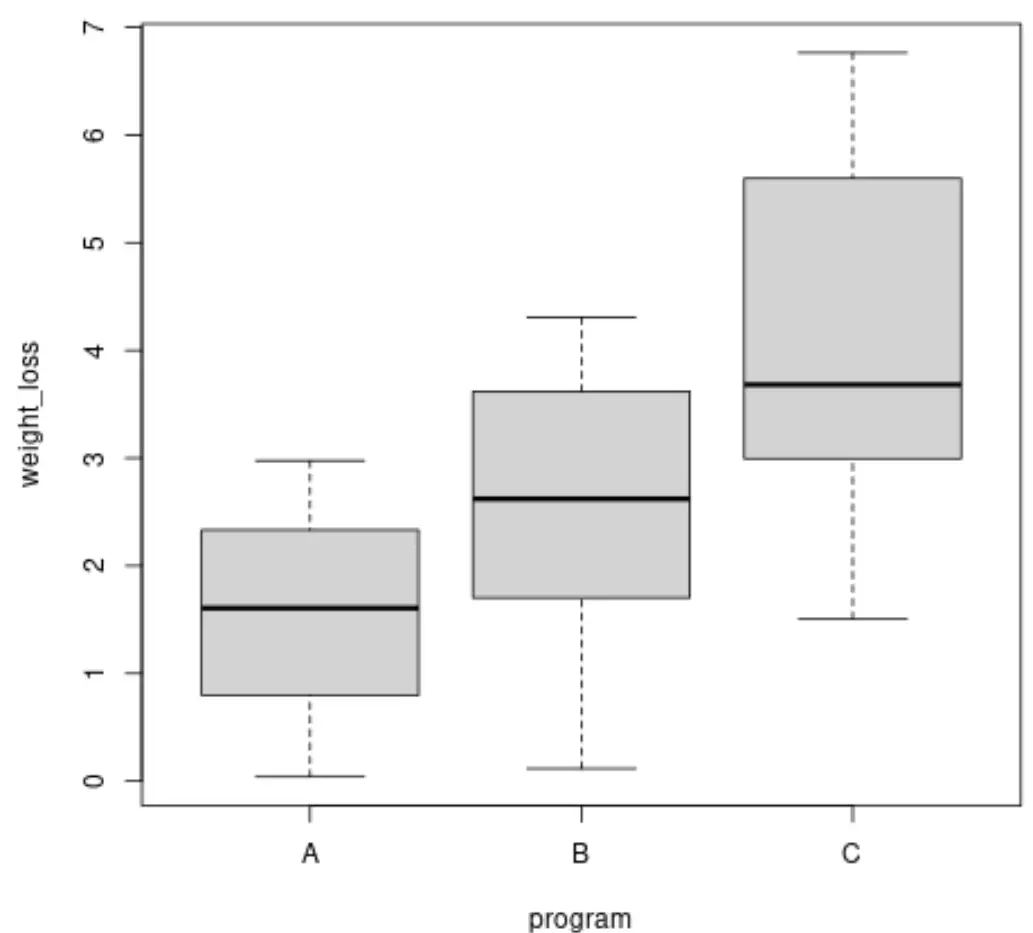
Kami juga dapat menghitung varian penurunan berat badan di setiap kelompok:

 #load dplyr package
library (dplyr)

#calculate variance of weight loss by group
data %>%
group_by (program) %>%
  summarize (var=var(weight_loss))

# A tibble: 3 x 2
  program var
     
1 A 0.819
2 B 1.53 
3 C 2.46

Kita dapat melihat bahwa varians antar kelompok berbeda, namun untuk menentukan apakah perbedaan ini signifikan secara statistik , kita dapat melakukan uji Brown-Forsythe.

Langkah 3: Lakukan tes Brown-Forsythe

Untuk melakukan pengujian Brown-Forsythe di R, kita dapat menggunakan fungsi bf.test() dari paket onewaytests :

 #load onewaytests package
library (onewaytests)

#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)

  Brown-Forsythe Test (alpha = 0.05) 
-------------------------------------------------- ----------- 
  data: weight_loss and program 

  statistic: 30.83304 
  num df: 2 
  name df: 74.0272 
  p.value: 1.816529e-10 

  Result: Difference is statistically significant. 
-------------------------------------------------- -----------

Nilai p dari tes tersebut ternyata kurang dari 0,000 dan, seperti yang ditunjukkan oleh hasilnya, perbedaan varian antara ketiga kelompok adalah signifikan secara statistik.

Langkah selanjutnya

Jika Anda tidak dapat menolak hipotesis nol uji Brown-Forsythe, maka Anda dapat melakukan ANOVA satu arah pada data tersebut.

Namun jika hipotesis nol ditolak, berarti asumsi persamaan varians dilanggar. Dalam hal ini, Anda memiliki dua opsi:

1. Tetap lakukan ANOVA satu arah.

Ternyata ANOVA satu arah sebenarnya kuat terhadap varian yang tidak sama asalkan varian terbesar tidak lebih besar dari 4 kali varian terkecil.

Pada langkah 2 contoh di atas, kita menemukan bahwa varian terkecil adalah 0,819 dan varian terbesar adalah 2,46. Jadi perbandingan varian terbesar dan terkecil adalah 2,46 / 0,819 = 3,003 .

Karena nilai ini kurang dari 4, kita cukup melakukan ANOVA satu arah.

2. Lakukan tes Kruskal-Wallis

Jika rasio varian terbesar dan varian terkecil lebih besar dari 4, seseorang dapat memilih untuk melakukan uji Kruskal-Wallis . Hal ini dianggap setara nonparametrik dari ANOVA satu arah.

Anda dapat menemukan contoh langkah demi langkah tes Kruskal-Wallis di R di sini .