Apa yang dimaksud dengan residu terstandar?
Residual adalah selisih antara nilai observasi dan nilai prediksi dalam model regresi .
Ini dihitung sebagai berikut:
Sisa = Nilai yang diamati – Nilai yang diprediksi
Jika kita memplot nilai observasi dan menempatkan garis regresi yang dipasang, residu untuk setiap observasi akan menjadi jarak vertikal antara observasi dan garis regresi:

Salah satu jenis residu yang sering kita gunakan untuk mengidentifikasi outlier dalam model regresi disebut residu terstandarisasi .
Ini dihitung sebagai berikut:
r i = e i / s( ei ) = e i / RSE√ 1-h ii
Emas:
- e i : Residu ke -i
- RSE: kesalahan standar sisa model
- h ii : Meningkatnya observasi ke-i
Dalam praktiknya, kita sering menganggap residu terstandar yang nilai absolutnya lebih besar dari 3 sebagai outlier.
Hal ini tidak berarti bahwa kita akan menghapus observasi tersebut dari model, namun setidaknya kita harus mempelajarinya lebih lanjut untuk memverifikasi bahwa observasi tersebut bukan merupakan hasil dari kesalahan entri data atau kejadian aneh lainnya.
Catatan: Terkadang residu yang distandarisasi juga disebut “residu yang dipelajari sendiri”.
Contoh: Cara menghitung residu terstandar
Misalkan kita memiliki kumpulan data berikut dengan total 12 observasi:

Jika kita menggunakan perangkat lunak statistik (seperti R , Excel , Python , Stata , dll.) untuk menyesuaikan garis regresi linier dengan kumpulan data ini, kita akan menemukan bahwa garis yang paling sesuai adalah:
kamu = 29,63 + 0,7553x
Dengan menggunakan baris ini, kita dapat menghitung nilai prediksi untuk setiap nilai Y berdasarkan nilai X. Misalnya, nilai prediksi observasi pertama adalah:
kamu = 29,63 + 0,7553*(8) = 35,67
Kami kemudian dapat menghitung sisa pengamatan ini sebagai berikut:
Sisa = Nilai teramati – Nilai prediksi = 41 – 35,67 = 5,33
Kita dapat mengulangi proses ini untuk mencari sisa setiap observasi:

Kita juga dapat menggunakan perangkat lunak statistik untuk menemukan bahwa kesalahan standar sisa model adalah 4,44 .
Dan, meskipun ini di luar cakupan tutorial ini, kita dapat menggunakan perangkat lunak untuk mencari statistik leverage (h ii ) untuk setiap observasi:
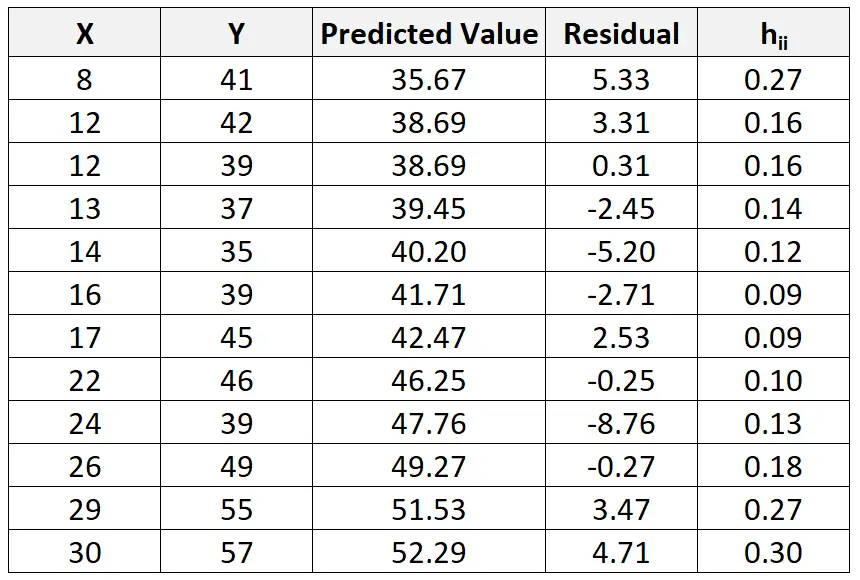
Kita kemudian dapat menggunakan rumus berikut untuk menghitung residu standar untuk setiap observasi:
r i = e i / RSE√ 1-jam ii
Misalnya, residu terstandar untuk observasi pertama dihitung sebagai berikut:
r saya = 5,33 / 4,44√ 1-0,27 = 1,404
Kita dapat mengulangi proses ini untuk menemukan residu terstandar untuk setiap observasi:
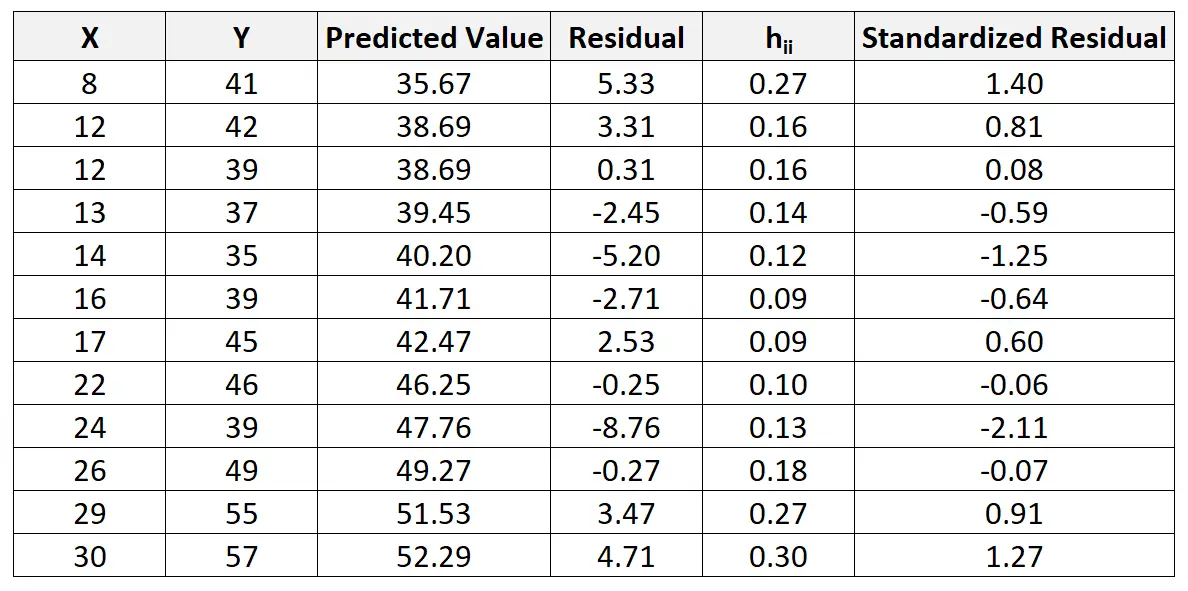
Kami kemudian dapat membuat plot sebar cepat dari nilai prediksi terhadap residu terstandar untuk melihat secara visual apakah ada residu terstandar yang melebihi ambang batas nilai absolut 3:
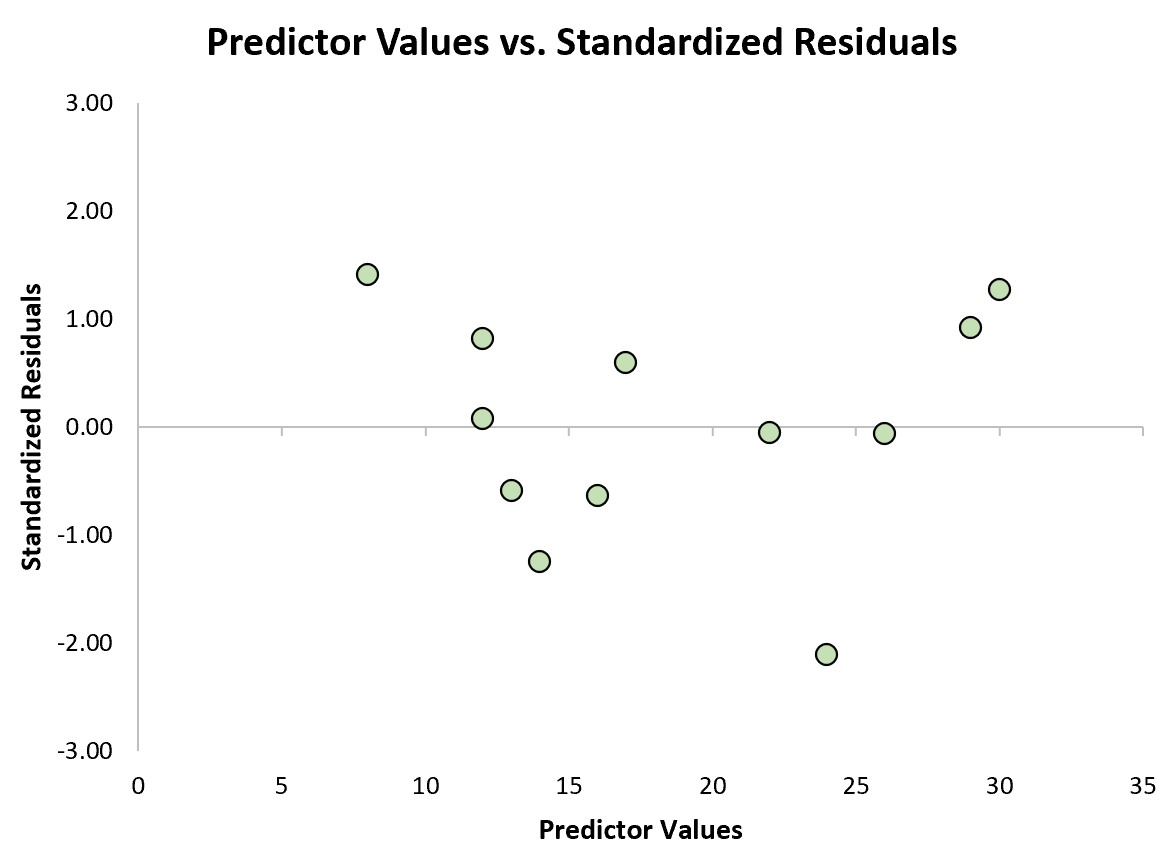
Dari grafik tersebut, kita dapat melihat bahwa tidak ada satu pun residu terstandar yang melebihi nilai absolut 3. Dengan demikian, tidak ada satu pun observasi yang tampak outlier.
Perlu dicatat bahwa dalam beberapa kasus, peneliti menganggap observasi yang residu terstandarnya melebihi nilai absolut 2 sebagai outlier.
Terserah Anda, bergantung pada bidang yang Anda kerjakan dan masalah spesifik yang sedang Anda kerjakan, apakah Anda ingin menggunakan nilai absolut 2 atau 3 sebagai ambang batas untuk outlier.
Sumber daya tambahan
Tutorial berikut memberikan informasi tambahan tentang residu terstandar:
Apa yang dimaksud dengan residu dalam statistik?
Cara menghitung residu standar di Excel
Cara menghitung residu standar di R
Cara Menghitung Residu Standar dengan Python