Apa yang dimaksud dengan fungsi massa probabilitas (pmf) dalam statistik?

Fungsi massa probabilitas , sering disingkat PMF , memberi tahu kita probabilitas suatu variabel acak diskrit mengambil nilai tertentu.

Misalnya kita melempar sebuah dadu sebanyak satu kali. Jika kita misalkan x menyatakan bilangan tempat dadu mendarat, maka peluang x sama dengan nilai yang berbeda dapat digambarkan sebagai berikut:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Ada peluang yang sama bahwa dadu akan mendarat di nomor mana pun antara 1 dan 6.

Berikut adalah cara kita menuliskan probabilitas ini sebagai fungsi massa probabilitas:

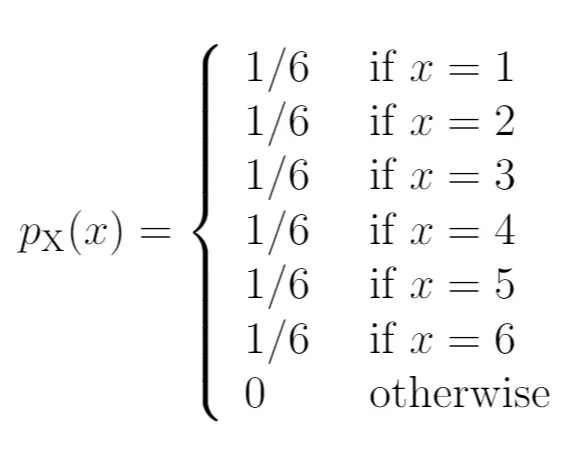
Sisi kiri diagram menunjukkan probabilitas yang terkait dengan hasil di sisi kanan:

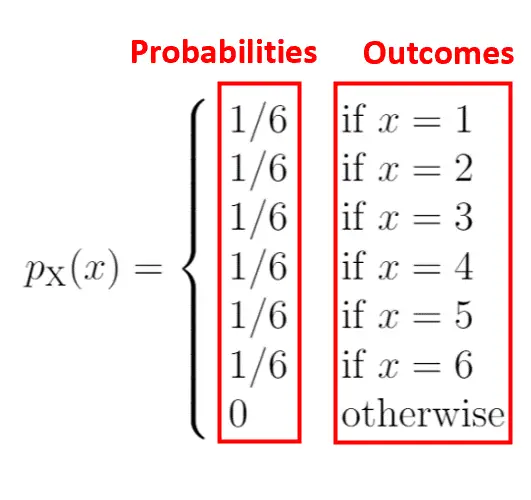
Karakteristik fungsi massa probabilitas adalah semua probabilitas harus berjumlah 1. Anda akan melihat bahwa PMF ini memenuhi kondisi berikut:

Jumlah probabilitas = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Dukungan untuk fungsi massa probabilitas mengacu pada himpunan nilai yang dapat diambil oleh variabel acak diskrit. Dalam contoh ini, dukungannya adalah {1, 2, 3, 4, 5, 6} karena nilai dadu dapat mengambil salah satu dari nilai tersebut.

Di luar support, nilai PMF adalah nol. Misalnya, peluang dadu mendarat di “0” atau “7” atau “8” adalah nol karena tidak satu pun dari angka-angka ini yang dimasukkan dalam tanda kurung.

Fungsi massa probabilitas dalam praktiknya

Dua contoh fungsi massa probabilitas yang paling umum dalam praktiknya berkaitan dengan distribusi binomial dan distribusi Poisson .

Distribusi binomial

Jika suatu variabel acak X mengikuti distribusi binomial, maka peluang keberhasilan X = k dapat dicari dengan rumus berikut:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Emas:

• n: jumlah percobaan
• k: jumlah keberhasilan
• p: probabilitas keberhasilan pada percobaan tertentu
• _n C _k : banyaknya cara untuk memperoleh k keberhasilan dalam n percobaan

Misalnya kita melempar sebuah koin sebanyak 3 kali. Kita dapat menggunakan rumus di atas untuk menentukan peluang munculnya gambar 0, 1, 2, dan 3 pada 3 pelemparan berikut:

• P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125
• P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 1 * 1 * (0,5) ² = 0,375
• P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 1 * 1 * (0,5) ¹ = 0,375
• P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 1 * (0,5) ⁰ = 0,125

Distribusi ikan

Jika suatu variabel acak X mengikuti distribusi Poisson, maka peluang keberhasilan X = k dapat dicari dengan rumus berikut:

P(X=k) = λ ^k * e ^{– λ} / k!

Emas:

• λ: jumlah rata-rata keberhasilan yang terjadi selama interval tertentu
• k: jumlah keberhasilan
• e: konstanta sama dengan sekitar 2,71828

Misalnya, sebuah rumah sakit tertentu mengalami rata-rata 2 kelahiran per jam. Kita dapat menggunakan rumus di atas untuk menentukan peluang mengalami kelahiran 0, 1, 2, 3, dst. dalam satu jam tertentu:

• P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353
• P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707
• P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707
• P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Lihat PMF

Kita sering memvisualisasikan fungsi massa probabilitas dengan grafik batang.

Misalnya, diagram batang berikut menunjukkan probabilitas yang terkait dengan jumlah kelahiran per jam untuk distribusi Poisson yang dijelaskan pada contoh sebelumnya:

Perhatikan bahwa jumlah kelahiran bisa bertambah hingga tak terhingga, namun probabilitasnya menjadi sangat kecil setelah 10 sehingga Anda bahkan tidak dapat melihatnya pada grafik batang.

Properti PMF

Fungsi massa probabilitas mempunyai sifat sebagai berikut:

1. Semua probabilitas mendukung positif. Misalnya, peluang munculnya sebuah dadu antara 1 dan 6 adalah positif, sedangkan peluang munculnya semua hasil lainnya adalah nol.

2. Semua hasil mempunyai peluang antara 0 dan 1. Misalnya, peluang munculnya sebuah dadu antara 1 dan 6 adalah 1/6, atau 0,1666666 untuk setiap hasil.

3. Jumlah semua peluang harus sama dengan 1. Misalnya, jumlah peluang munculnya sebuah dadu pada suatu angka tertentu adalah 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.

Sumber daya tambahan

Apa itu variabel acak?
CDF atau PDF: apa bedanya?
Pengenalan distribusi binomial
Pengenalan distribusi Poisson