Peristiwa yang saling inklusif atau saling eksklusif
Dua peristiwa dikatakan saling lepas jika peristiwa-peristiwa tersebut tidak dapat terjadi secara bersamaan.
Misalkan kejadian A adalah kejadian sebuah dadu mendarat di bilangan genap dan kejadian B adalah kejadian sebuah dadu mendarat di bilangan ganjil.
Kami akan mendefinisikan ruang sampel untuk acara sebagai berikut:
- SEBUAH = {2, 4, 6}
- B = {1, 3, 5}
Perhatikan bahwa tidak ada tumpang tindih antara dua ruang sampel. Jadi kejadian A dan B saling lepas karena tidak mungkin keduanya terjadi secara bersamaan. Angka yang jatuh pada sebuah dadu tidak boleh genap dan ganjil.
Sebaliknya, dua peristiwa dikatakan saling inklusif jika peristiwa-peristiwa tersebut dapat terjadi pada waktu yang bersamaan.
Misalnya, kejadian C adalah kejadian munculnya sebuah dadu pada bilangan genap dan kejadian D adalah kejadian munculnya dadu pada bilangan genap lebih dari 3.
Kami akan mendefinisikan ruang sampel untuk acara sebagai berikut:
- C = {2, 4, 6}
- d = {4, 5, 6}
Perhatikan bahwa ada tumpang tindih antara dua ruang sampel. Jadi, kejadian C dan D sama-sama inklusif karena bisa terjadi pada waktu yang bersamaan. Ada kemungkinan dadu mendarat pada angka genap lebih besar dari 3.
Kemungkinan kejadian
Jika dua kejadian saling lepas, maka peluang terjadinya keduanya adalah nol.
Misalnya, perhatikan dua contoh ruang untuk kejadian A dan B di atas:
- SEBUAH = {2, 4, 6}
- B = {1, 3, 5}
Karena tidak ada tumpang tindih dalam ruang sampel, kita katakan P(A dan B) = 0 .
Namun jika dua kejadian saling inklusif , maka peluang terjadinya keduanya akan lebih besar dari nol.
Misalnya, perhatikan dua contoh ruang untuk kejadian C dan D sebelumnya:
- C = {2, 4, 6}
- d = {4, 5, 6}
Karena ada 6 angka yang memungkinkan untuk mendaratkan dadu dan dua dari angka tersebut (4 dan 6) termasuk dalam kejadian C dan D, kita akan menghitung P(C dan D) sebagai 2/6, atau 1/3 .
Lihat acara yang saling inklusif dan saling eksklusif
Kita sering menggunakan diagram Venn untuk memvisualisasikan probabilitas yang terkait dengan peristiwa.
Jika dua kejadian saling lepas, maka keduanya tidak akan tumpang tindih sama sekali dalam diagram Venn:
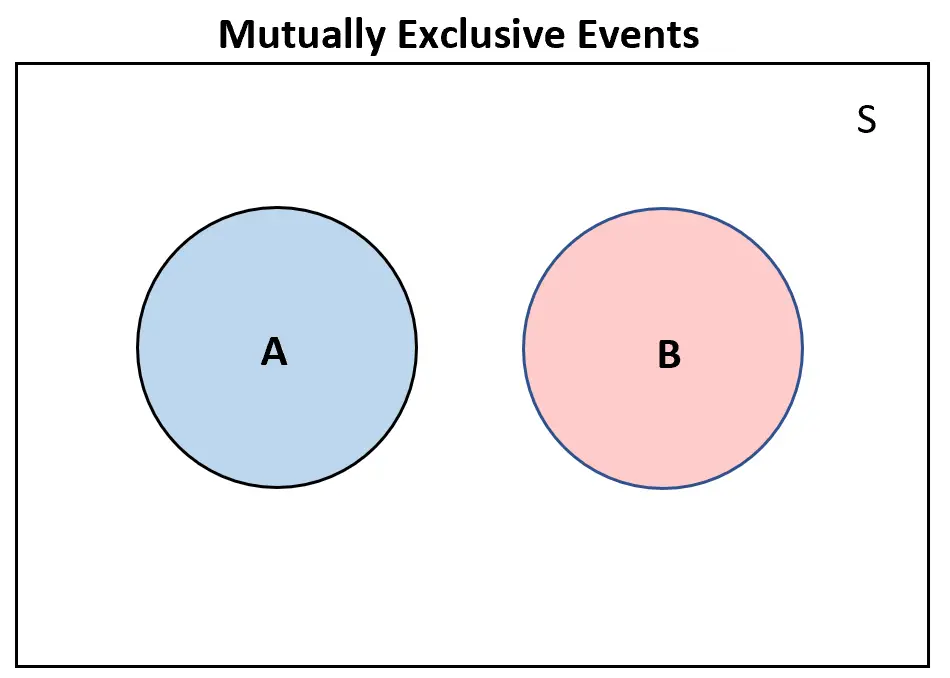
Sebaliknya, jika dua peristiwa saling inklusif , setidaknya akan ada beberapa tumpang tindih dalam diagram Venn:
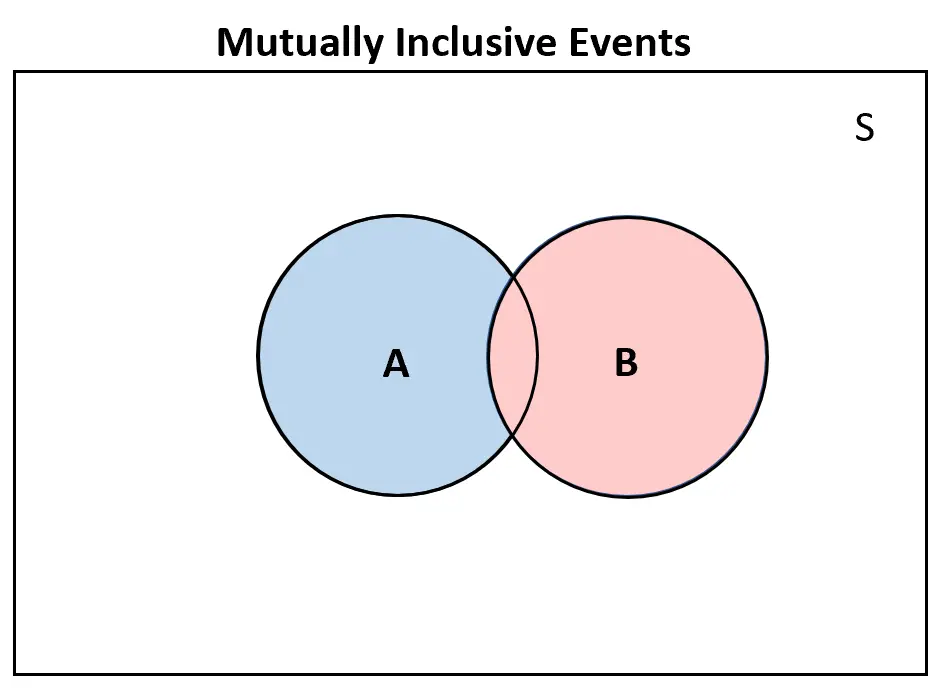
Sumber daya tambahan
Pengantar probabilitas teoretis
Aturan umum perkalian
Apa yang dimaksud dengan peristiwa yang saling lepas?