Apa tes q cochran? (definisi & #038; contoh)

Uji Cochran’s Q merupakan uji statistik yang digunakan untuk menentukan apakah proporsi “keberhasilan” sama pada tiga kelompok atau lebih di mana muncul individu yang sama pada setiap kelompok.

Misalnya, kita dapat menggunakan tes Cochran’s Q untuk menentukan apakah proporsi siswa yang lulus suatu tes sama ketika menggunakan tiga teknik belajar yang berbeda.

Langkah-langkah Melakukan Tes Q Cochran

Uji Q Cochran menggunakan hipotesis nol dan hipotesis alternatif berikut:

Hipotesis nol (H ₀ ): Proporsi “keberhasilan” adalah sama di semua kelompok

Hipotesis alternatif ( _HA ): Proporsi “keberhasilan” berbeda pada setidaknya satu kelompok

Statistik uji dihitung sebagai berikut:

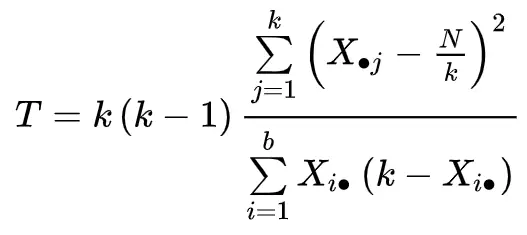
Emas:

• k : Jumlah perlakuan (atau “kelompok”)
• Xj : jumlah kolom perlakuan ^ke-j
• b: Jumlah blok
• Xi. : Total baris untuk blok ^ke-i
• N: Total keseluruhan

Statistik uji T mengikuti distribusi Chi-kuadrat dengan derajat kebebasan k-1 .

Jika nilai p yang terkait dengan statistik uji berada di bawah tingkat signifikansi tertentu (seperti α = 0,05), kita dapat menolak hipotesis nol dan menyimpulkan bahwa kita memiliki cukup bukti untuk mengatakan bahwa proporsi “keberhasilan” berbeda dalam setidaknya salah satu kelompok.

Contoh : Uji Q Cochran

Misalkan seorang peneliti ingin mengetahui apakah tiga teknik belajar yang berbeda menghasilkan proporsi tingkat keberhasilan yang berbeda di kalangan siswa.

Untuk mengujinya, ia merekrut 20 siswa yang masing-masing mengikuti ujian dengan tingkat kesulitan yang sama menggunakan tiga teknik belajar yang berbeda. Hasilnya ditunjukkan di bawah ini:

Untuk melakukan uji Cochran’s Q, kita dapat menggunakan perangkat lunak statistik karena akan membosankan jika dilakukan secara manual.

Berikut adalah kode yang dapat kita gunakan untuk membuat dataset ini dan melakukan uji Cochran’s Q dalam bahasa pemrograman statistik R:

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

Dari hasil pengujian kita dapat mengamati hal-hal berikut:

• Statistik ujinya adalah 0,333
• Nilai p yang sesuai adalah 0,8465

Karena nilai p ini tidak kurang dari 0,05, kita gagal menolak hipotesis nol.

Ini berarti bahwa kita tidak memiliki cukup bukti untuk mengatakan bahwa teknik belajar yang digunakan oleh siswa menghasilkan proporsi tingkat keberhasilan yang berbeda-beda.