Korelasi vs regresi: apa bedanya?

Korelasi dan regresi adalah dua istilah statistik yang berkaitan, namun tidak sepenuhnya sama.

Dalam tutorial ini, kami akan memberikan penjelasan singkat tentang kedua istilah tersebut dan menjelaskan persamaan dan perbedaannya.

Apa itu korelasi?

Korelasi mengukur hubungan linier antara dua variabel, x dan y . Ini memiliki nilai antara -1 dan 1 di mana:

• -1 menunjukkan korelasi linier negatif sempurna antara dua variabel
• 0 menunjukkan tidak ada korelasi linier antara dua variabel
• Angka 1 menunjukkan korelasi linier positif sempurna antara dua variabel

Misalnya, kita mempunyai kumpulan data berikut yang berisi dua variabel: (1) Jam belajar dan (2) Nilai ujian yang diterima untuk 20 siswa berbeda:

Jika kita membuat diagram sebar jam belajar versus hasil ujian, tampilannya akan seperti ini:

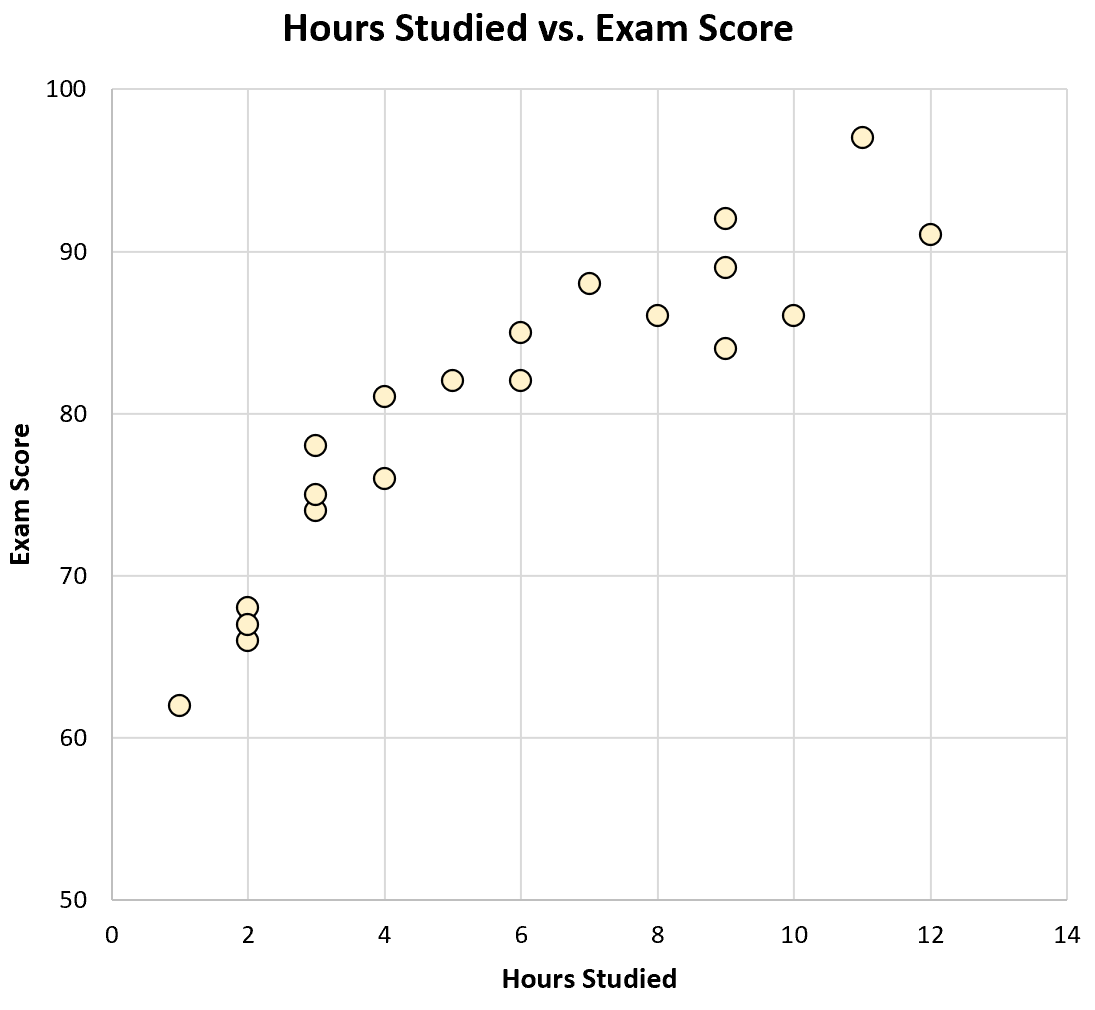
Hanya dengan melihat grafiknya, kita dapat melihat bahwa siswa yang belajar lebih banyak cenderung memiliki nilai ujian yang lebih baik. Dengan kata lain secara visual kita dapat melihat adanya korelasi positif antara kedua variabel tersebut.

Dengan menggunakan kalkulator, kita dapat melihat bahwa korelasi kedua variabel tersebut adalah r = 0,915 . Nilai yang mendekati 1 berarti terdapat korelasi positif yang kuat antara kedua variabel.

Apa itu regresi?

Regresi adalah metode yang dapat kita gunakan untuk memahami bagaimana perubahan nilai variabel x mempengaruhi nilai variabel y .

Model regresi menggunakan satu variabel, x , sebagai variabel prediktor dan variabel lainnya, y , sebagai variabel respon . Kemudian ditemukan persamaan dengan bentuk berikut yang paling menggambarkan hubungan antara dua variabel:

ŷ = b ₀ + b ₁ x

Emas:

• ŷ : nilai prediksi variabel respon
• b ₀ : Ordinat di titik asal (nilai y ketika x sama dengan nol)
• b ₁ : Koefisien regresi (rata-rata kenaikan y untuk kenaikan satu satuan x)
• x : nilai variabel prediktif

Misalnya, pertimbangkan kumpulan data kami sebelumnya:

Dengan menggunakan kalkulator regresi linier , kami menemukan bahwa persamaan berikut paling menggambarkan hubungan antara kedua variabel ini:

Prediksi nilai ujian = 65,47 + 2,58*(jam belajar)

Cara menafsirkan persamaan ini adalah:

• Prediksi nilai ujian siswa yang belajar nol jam adalah 65,47 .
• Rata-rata peningkatan nilai ujian yang terkait dengan tambahan jam belajar adalah 2,58 .

Kita juga dapat menggunakan persamaan ini untuk memprediksi skor yang akan diterima siswa berdasarkan jumlah jam belajar.

Misalnya, seorang siswa yang belajar 6 jam seharusnya mendapat nilai 80,95 :

Prediksi nilai ujian = 65.47 + 2.58*(6) = 80.95 .

Kita juga dapat memplot persamaan ini sebagai garis pada plot sebar:

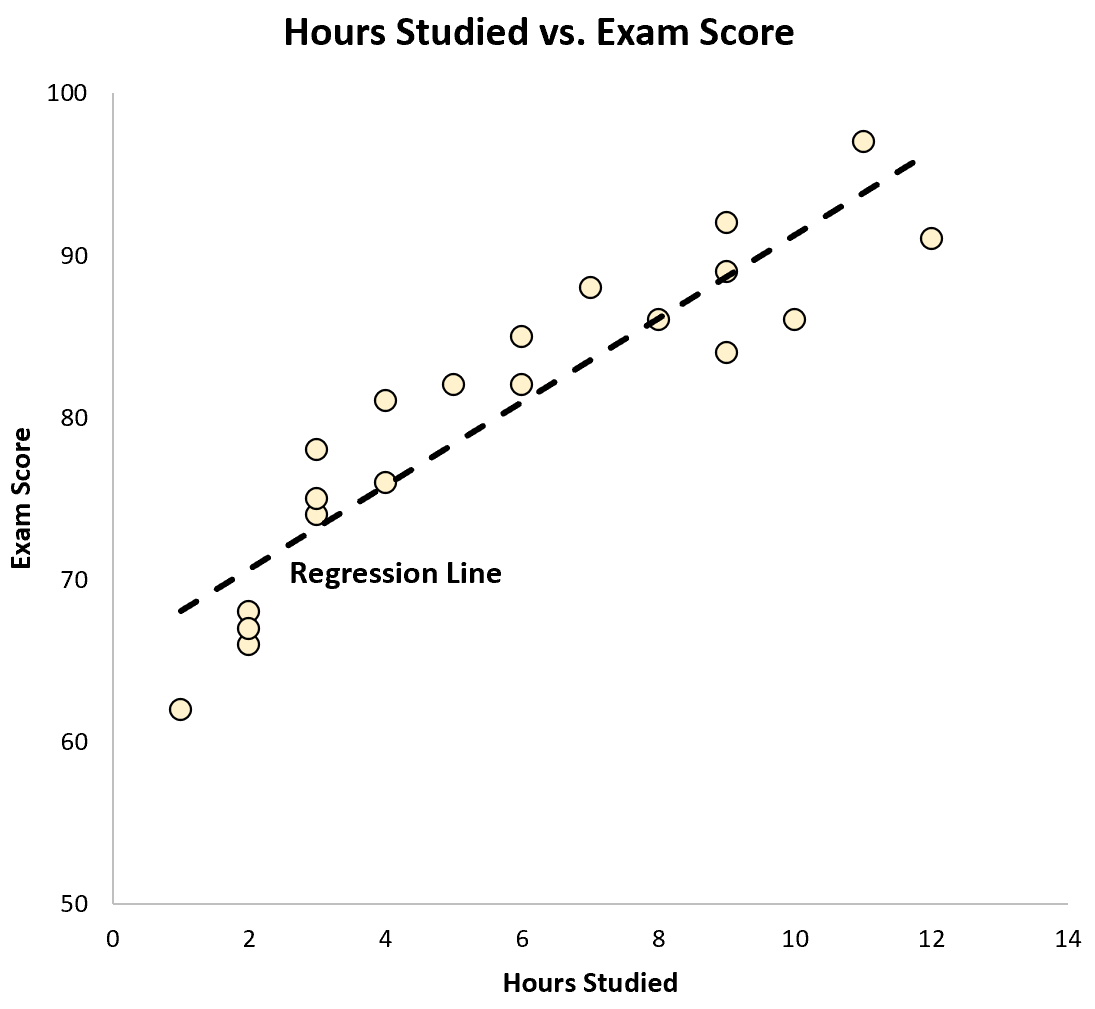
Kita dapat melihat bahwa garis regresi “cocok” dengan data dengan cukup baik.

Ingat sebelumnya bahwa korelasi antara kedua variabel adalah r = 0,915 . Ternyata kita dapat mengkuadratkan nilai tersebut dan mendapatkan suatu bilangan yang disebut “r kuadrat” yang menggambarkan proporsi total varians pada variabel respon yang dapat dijelaskan oleh variabel prediktor.

Dalam contoh ini, r ² = 0,915 ² = 0,837 . Artinya 83,7% variasi nilai ujian dapat dijelaskan oleh jumlah jam belajar.

Korelasi vs regresi: persamaan dan perbedaan

Berikut rangkuman persamaan dan perbedaan korelasi dan regresi:

Kesamaan:

• Keduanya mengukur arah hubungan antara dua variabel.
• Keduanya mengukur kekuatan hubungan antara dua variabel.

Perbedaan:

• Regresi mampu menunjukkan hubungan sebab akibat antara dua variabel. Korelasi tidak melakukan hal itu.
• Regresi dapat menggunakan persamaan untuk memprediksi nilai suatu variabel berdasarkan nilai variabel lainnya. Korelasi tidak melakukan hal itu.
• Regresi menggunakan persamaan untuk mengukur hubungan antara dua variabel. Korelasi menggunakan satu angka.

Sumber daya tambahan

Tutorial berikut menawarkan penjelasan lebih mendalam tentang topik yang dibahas dalam artikel ini.

Pengantar Koefisien Korelasi Pearson
Pengantar Regresi Linier Sederhana
Kalkulator Regresi Linier Sederhana
Berapa nilai R-kuadrat yang bagus?