Distribusi normal terbalik: pengertian & contoh
Istilah distribusi normal terbalik mengacu pada metode penggunaan probabilitas yang diketahui untuk menemukan nilai kritis z yang sesuai dalam distribusi normal .
Hal ini berbeda dengan distribusi Gaussian terbalik , yang merupakan distribusi probabilitas kontinu.
Tutorial ini memberikan beberapa contoh penggunaan distribusi normal terbalik dalam perangkat lunak statistik yang berbeda.
Distribusi normal terbalik kita memiliki kalkulator TI-83 atau TI-84
Kemungkinan besar Anda akan menemukan istilah “distribusi normal terbalik” pada kalkulator TI-83 atau TI-84, yang menggunakan fungsi berikut untuk mencari nilai kritis z yang sesuai dengan probabilitas tertentu:
invNorm(probabilitas, μ, σ)
Emas:
- probabilitas: tingkat signifikansi
- μ: rata-rata populasi
- σ: deviasi standar populasi
Anda dapat mengakses fungsi ini pada kalkulator TI-84 dengan menekan 2nd lalu menekan vars . Ini akan membawa Anda ke layar DISTR tempat Anda kemudian dapat menggunakan invNorm() :

Misalnya, kita dapat menggunakan fungsi ini untuk mencari nilai kritis z yang sesuai dengan nilai probabilitas 0,05:
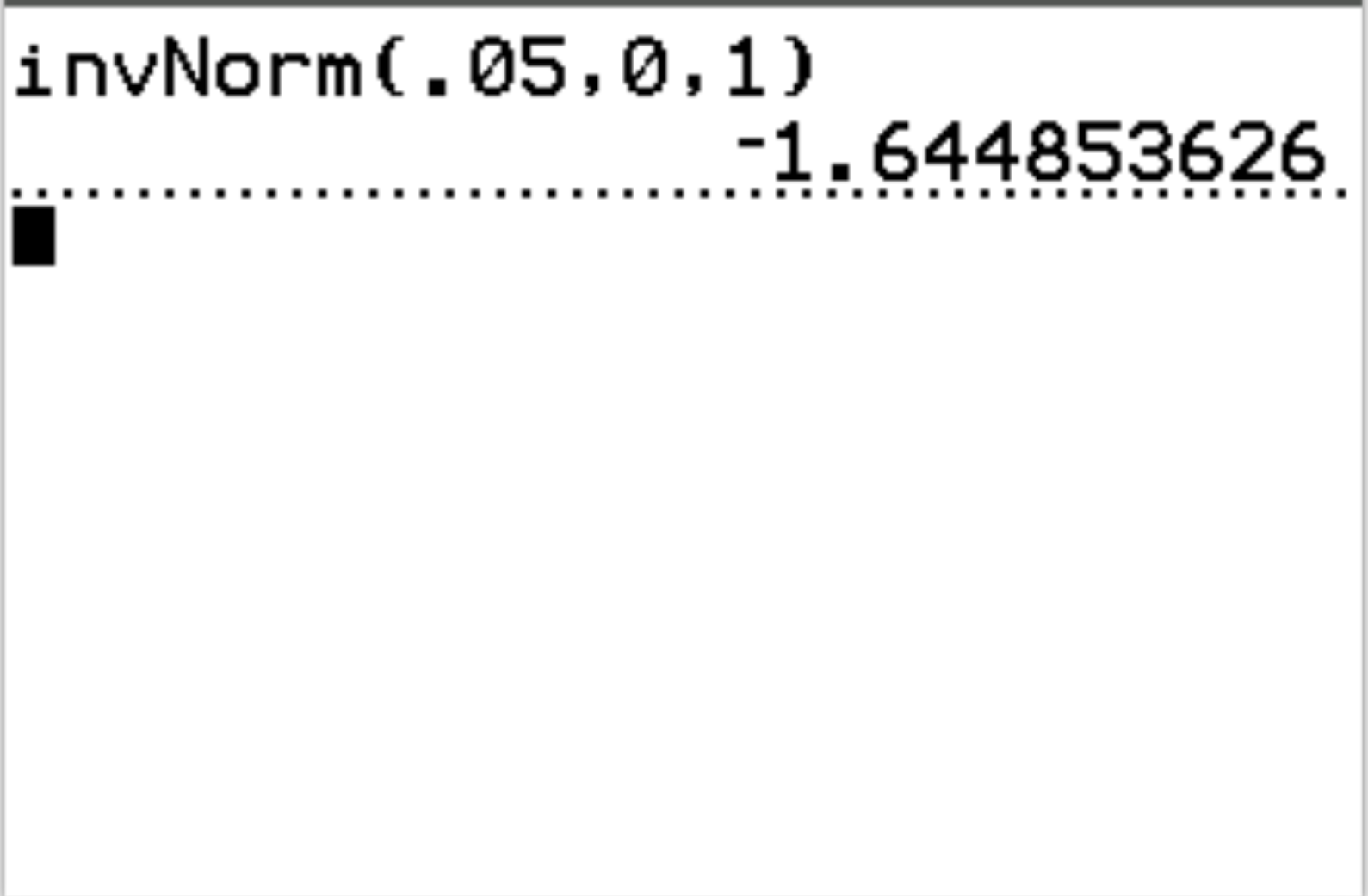
Nilai z kritis yang sesuai dengan nilai probabilitas 0,05 adalah -1,64485 .
Terkait: Cara Menggunakan invNorm pada Kalkulator TI-84 (Dengan Contoh)
Distribusi Normal Terbalik di Excel
Untuk mencari nilai kritis z yang terkait dengan nilai probabilitas tertentu di Excel, kita dapat menggunakan fungsi INVNORM() yang menggunakan sintaks berikut:
INVNORM(p, rata-rata, sd)
Emas:
- p: tingkat signifikansi
- rata-rata: rata-rata populasi
- sd: simpangan baku populasi
Misalnya, kita dapat menggunakan fungsi ini untuk mencari nilai kritis z yang sesuai dengan nilai probabilitas 0,05:
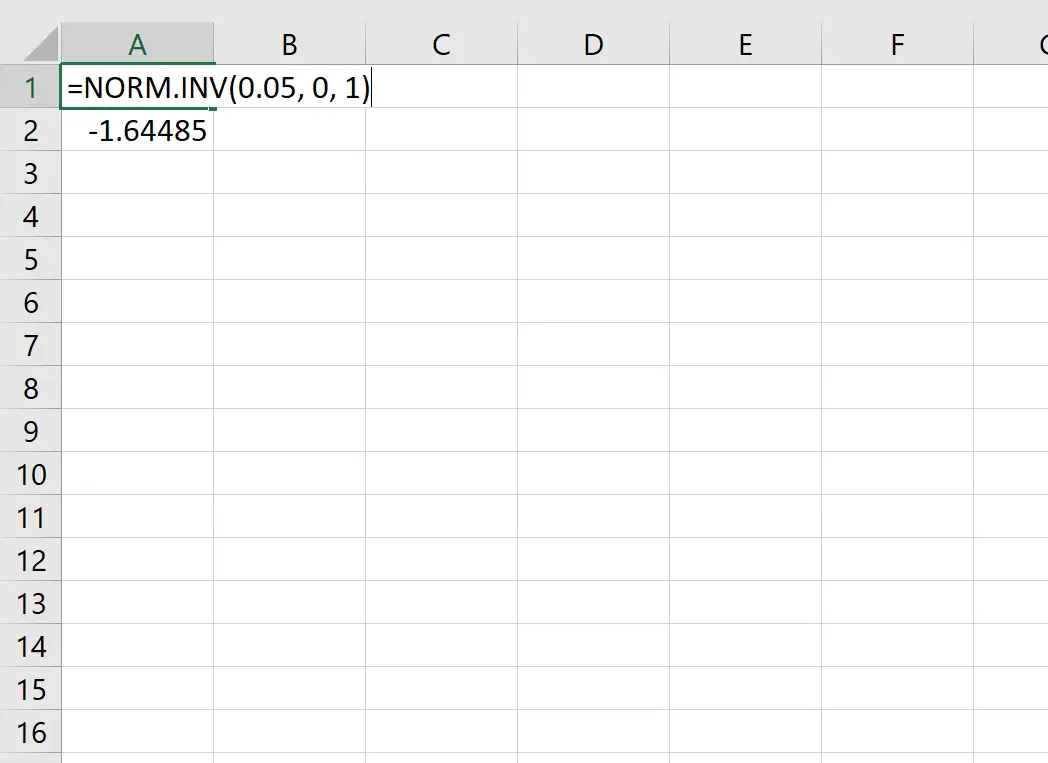
Nilai z kritis yang sesuai dengan nilai probabilitas 0,05 adalah -1,64485 .
Distribusi normal terbalik di R
Untuk mencari nilai kritis z yang terkait dengan nilai probabilitas tertentu di R, kita dapat menggunakan fungsi qnorm() , yang menggunakan sintaks berikut:
qnorm (p, mean, sd)
Emas:
- p: tingkat signifikansi
- rata-rata: rata-rata populasi
- sd: simpangan baku populasi
Misalnya, kita dapat menggunakan fungsi ini untuk mencari nilai kritis z yang sesuai dengan nilai probabilitas 0,05:
qnorm (p= .05 , mean= 0 , sd= 1 ) [1] -1.644854
Sekali lagi, nilai z kritis yang sesuai dengan nilai probabilitas 0,05 adalah -1,64485 .