R multiple atau r square: apa bedanya?

Saat Anda menyesuaikan model regresi menggunakan sebagian besar perangkat lunak statistik, Anda akan sering melihat dua nilai berikut pada hasilnya:

Multiple R: koefisien korelasi berganda antara tiga variabel atau lebih.

R-Square: Ini dihitung sebagai (Multiple R) ² dan mewakili proporsi varians variabel respon model regresi yang dapat dijelaskan oleh variabel prediktor. Nilai ini bervariasi dari 0 hingga 1.

Dalam praktiknya, kita sering kali tertarik pada nilai R-kuadrat karena nilai tersebut menunjukkan seberapa berguna variabel prediktor dalam memprediksi nilai variabel respons.

Namun, setiap kali kita menambahkan variabel prediktor baru ke dalam model, R-squared dijamin akan meningkat meskipun variabel prediktor tidak berguna.

R-squared yang disesuaikan adalah versi modifikasi dari R-squared yang menyesuaikan jumlah prediktor dalam model regresi. Ini dihitung sebagai berikut:

Disesuaikan R ² = 1 – [(1-R ² )*(n-1)/(nk-1)]

Emas:

• R ² : R ² model
• n : Jumlah pengamatan
• k : Banyaknya variabel prediktor

Karena R-kuadrat selalu meningkat seiring Anda menambahkan lebih banyak prediktor ke model, R-kuadrat yang disesuaikan dapat berfungsi sebagai metrik yang memberi tahu Anda seberapa berguna suatu model, disesuaikan berdasarkan jumlah prediktor dalam suatu model .

Untuk lebih memahami masing-masing istilah tersebut, perhatikan contoh berikut.

Contoh: Kelipatan R, R-kuadrat, dan R-kuadrat yang disesuaikan

Misalkan kita memiliki kumpulan data berikut yang berisi tiga variabel berikut untuk 12 siswa berbeda:

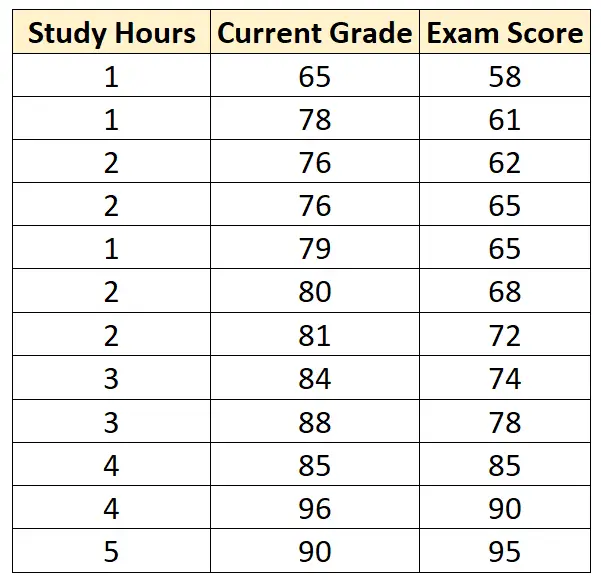
Misalkan kita memasang model regresi linier berganda dengan menggunakan jam belajar dan nilai saat ini sebagai variabel prediktor dan nilai ujian sebagai variabel respon dan memperoleh hasil sebagai berikut:

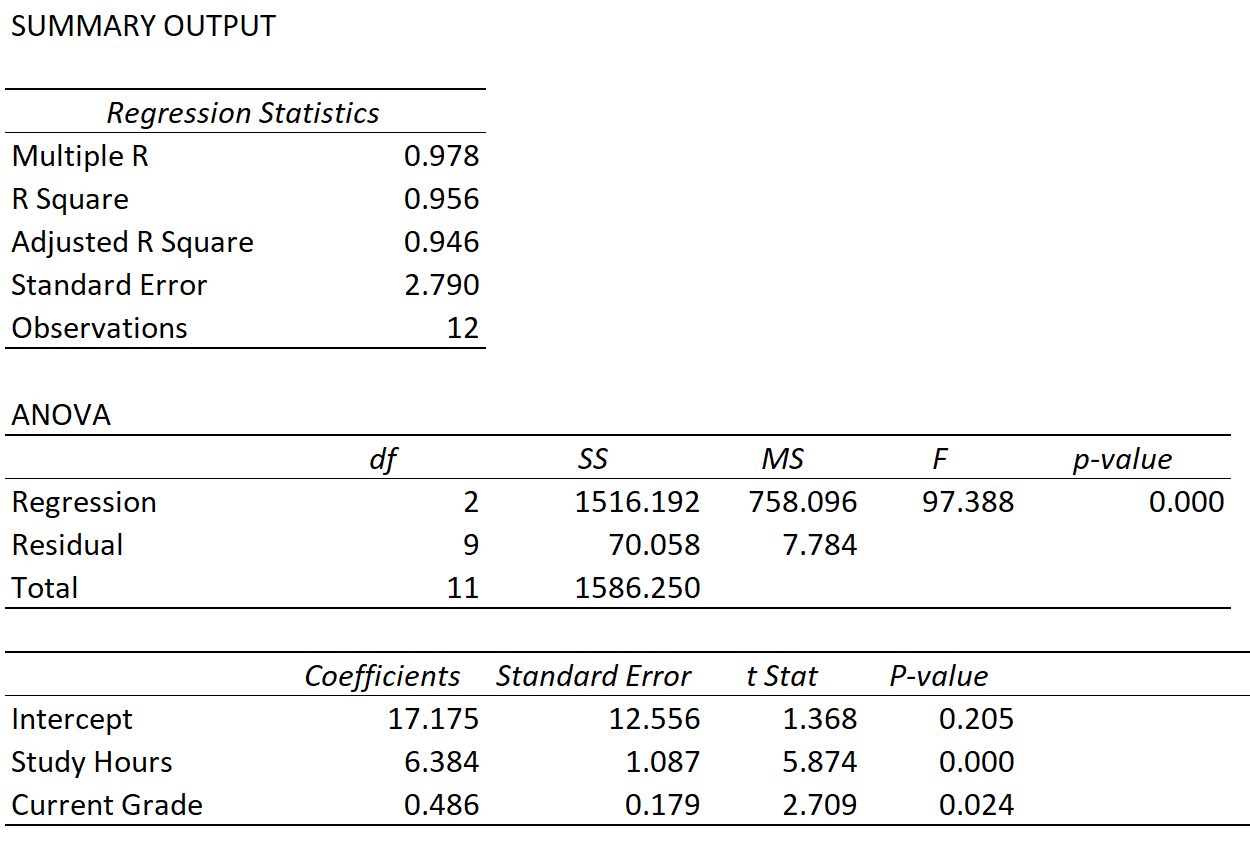
Kita dapat mengamati nilai dari tiga metrik berikut:

Kelipatan R : 0,978 . Ini mewakili korelasi ganda antara variabel respon dan dua variabel prediktor.

R Persegi: 0,956 . Ini dihitung sebagai (Kelipatan R) ² = (0,978) ² = 0,956. Hal ini menunjukkan bahwa 95,6% variasi nilai ujian dapat dijelaskan oleh jumlah jam yang dihabiskan siswa untuk belajar dan nilai mereka saat ini dalam mata pelajaran tersebut.

R-kuadrat yang disesuaikan: 0,946 . Ini dihitung sebagai berikut:

Disesuaikan R ² = 1 – [(1-R ² )*(n-1)/(nk-1)] = 1 – [(1-.956)*(12-1)/(12-2-1) ] = 0,946.

Ini mewakili nilai R-kuadrat yang disesuaikan dengan jumlah variabel prediktor dalam model .

Ukuran ini akan berguna jika, misalnya, kita menyesuaikan model regresi lain dengan 10 prediktor dan menemukan bahwa R-kuadrat yang disesuaikan dari model tersebut adalah 0,88 . Hal ini menunjukkan bahwa model regresi dengan dua prediktor saja lebih baik karena memiliki nilai R square yang disesuaikan lebih tinggi.

Sumber daya tambahan

Pengantar Regresi Linier Berganda
Berapa nilai R-kuadrat yang bagus?