Hukum probabilitas total: definisi & contoh

Dalam teori probabilitas, hukum probabilitas total adalah cara yang berguna untuk mencari probabilitas suatu kejadian A ketika kita tidak mengetahui secara langsung probabilitas A tetapi kita mengetahui bahwa kejadian B ₁ , B ₂ , B ₃ … membentuk sebuah partisi. dari ruang sampel S.

Undang-undang ini menetapkan hal-hal berikut:

Hukum probabilitas total

Jika B ₁ , B ₂ , B ₃ … membentuk partisi ruang sampel S , maka peluang kejadian A dapat dihitung sebagai berikut:

P( A ) = ΣP( A | B _i )*P( B _i )

Cara termudah untuk memahami hukum ini adalah dengan mengambil contoh sederhana.

Misalkan ada dua kantong dalam sebuah kotak berisi kelereng berikut:

• Kantong 1 : 7 kelereng merah dan 3 kelereng hijau
• Kantong 2 : 2 kelereng merah dan 8 kelereng hijau

Jika kita memilih salah satu kantong secara acak, kemudian secara acak mengambil kelereng dari kantong tersebut, berapakah peluang terambilnya kelereng berwarna hijau?

Dalam contoh ini, misalkan P( G ) = peluang terambilnya kelereng hijau. Kemungkinan itulah yang menarik perhatian kita, namun kita tidak dapat menghitungnya secara langsung.

Sebagai gantinya, kita perlu menggunakan probabilitas bersyarat dari G , jika ada kejadian B di mana B _i membentuk partisi ruang sampel S. Dalam contoh ini, kita mempunyai probabilitas bersyarat berikut:

• P(G| _B1 ) = 3/10 = 0,3
• P(G| _B2 ) = 8/10 = 0,8

Jadi, dengan menggunakan hukum peluang total, kita dapat menghitung peluang terambilnya kelereng hijau sebagai berikut:

• P(G) = ΣP(G|B _i )*P(B _i )
• P(G) = P(G|B ₁ )*P(B ₁ ) + P(G|B ₂ )*P(B ₂ )
• P(G) = (0,3)*(0,5) + (0,8)*(0,5)
• P(G) = 0,55

Jika kita memilih salah satu kantong secara acak, lalu secara acak memilih kelereng dari kantong tersebut, peluang terambilnya kelereng hijau adalah 0,55 .

Bacalah dua contoh berikut untuk memperkuat pemahaman Anda tentang hukum probabilitas total.

Contoh 1: Widget

Perusahaan A memasok 80% widget ke bengkel mobil dan hanya 1% widgetnya yang rusak. Perusahaan B memasok 20% sisa widget ke bengkel mobil dan 3% widgetnya rusak.

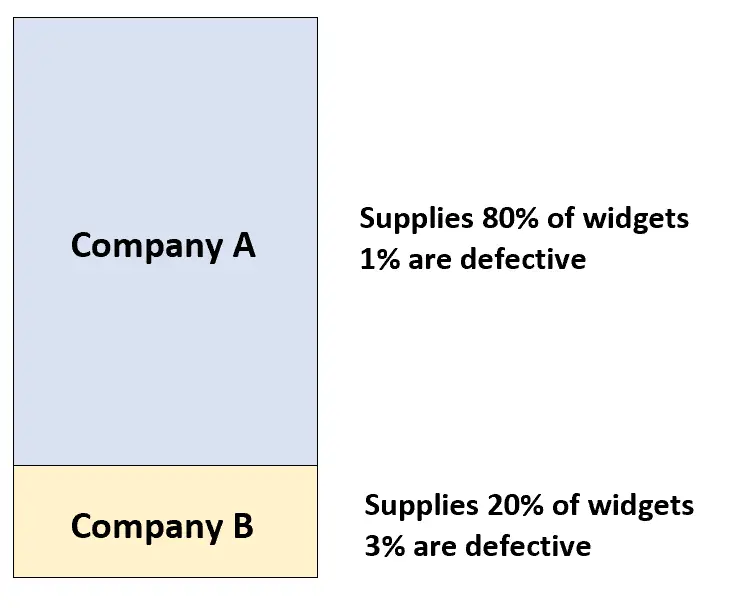
Jika seorang pelanggan secara acak membeli widget dari bengkel mobil, berapa probabilitas widget tersebut rusak?

Jika kita misalkan P( D ) = probabilitas suatu widget rusak dan P(B _i ) probabilitas bahwa widget tersebut berasal dari salah satu perusahaan, maka kita dapat menghitung probabilitas pembelian widget yang rusak sebagai berikut:

• P(D) = ΣP(D|B _i )*P(B _i )
• P(D) = P(D|B ₁ )*P(B ₁ ) + P(D|B ₂ )*P(B ₂ )
• P(D) = (0,01)*(0,80) + (0,03)*(0,20)
• P(D) = 0,014

Jika kita membeli widget secara acak dari toko mobil ini, kemungkinan widget tersebut rusak adalah 0,014 .

Contoh 2: Hutan

Hutan A menempati 50% dari total luas taman tertentu, dan 20% tanaman di hutan ini beracun. Hutan B menempati 30% dari total luas dan 40% tanaman yang dikandungnya beracun. Hutan C menempati 20% sisa wilayah dan 70% tanaman yang ditemukan di sana beracun.

Jika kita secara acak masuk ke taman ini dan memetik tanaman dari tanah, seberapa besar kemungkinan tanaman tersebut beracun?

Jika kita misalkan P( P ) = peluang tanaman tersebut beracun, dan P(B _i ) peluang bahwa kita telah memasuki salah satu dari tiga hutan, maka kita dapat menghitung peluang bahwa tanaman yang dipilih secara acak beracun seperti:

• P(P) = ΣP(P|B _i )*P(B _i )
• P(P) = P(P|B ₁ )*P(B ₁ ) + P(P|B ₂ )*P(B ₂ ) + P(P|B ₃ )*P(B ₃ )
• P(P) = (0,20)*(0,50) + (0,40)*(0,30) + (0,70)*(0,20)
• P(P) = 0,36

Jika kita memilih tanaman secara acak dari dalam tanah, kemungkinan tanaman tersebut beracun adalah 0,36 .

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang topik probabilitas:

Bagaimana mencari mean dari distribusi probabilitas
Bagaimana mencari simpangan baku dari suatu distribusi probabilitas
Kalkulator Distribusi Probabilitas