Berapa rata-rata marjinal? (definisi & #038; contoh)

Dalam tabel kontingensi, rata-rata marjinal suatu variabel adalah rata-rata variabel tersebut pada setiap tingkat variabel lainnya.

Seperti namanya, rata-rata ini muncul di pinggir tabel kontingensi.

Contoh berikut menunjukkan cara menghitung rata-rata marjinal untuk tabel kontingensi tertentu.

Contoh: Perhitungan rata-rata marjinal

Tabel kontingensi berikut menunjukkan nilai ujian rata-rata 100 siswa yang menggunakan tiga teknik belajar berbeda untuk mempersiapkan ujian.

Baris menampilkan jenis kelamin siswa dan kolom menampilkan teknik belajar yang mereka gunakan:

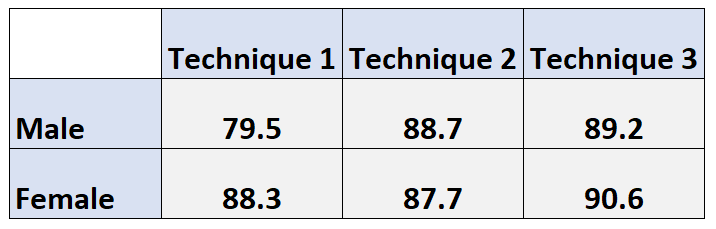
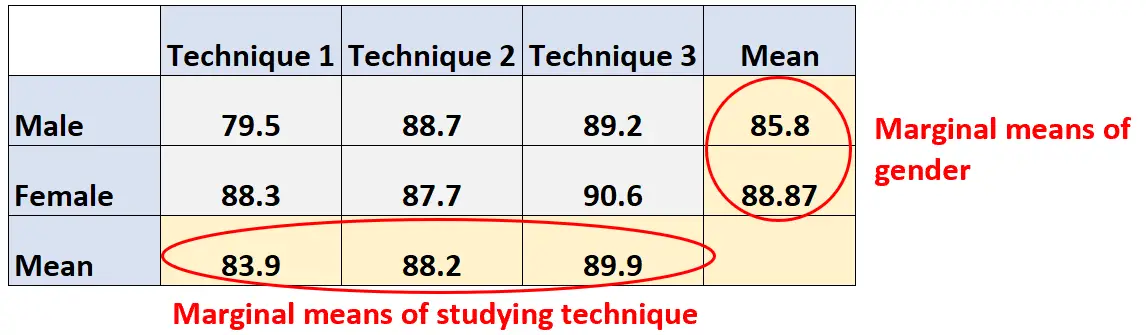
Rata-rata marjinal gender hanyalah rata-rata setiap tingkat gender untuk setiap tingkat teknik pembelajaran.

Misalnya, rata-rata nilai ujian marjinal untuk pria dihitung sebagai berikut:

Rata-rata marjinal untuk pria: (79,5 + 88,7 + 89,2) / 3 = 85,8

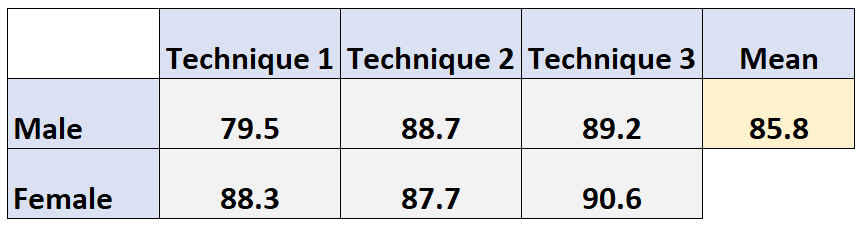
Demikian pula, nilai ujian rata-rata marjinal untuk perempuan dihitung sebagai berikut:

Rata-rata marjinal perempuan: (88,3 + 87,7 + 90,6) / 3 = 88,87

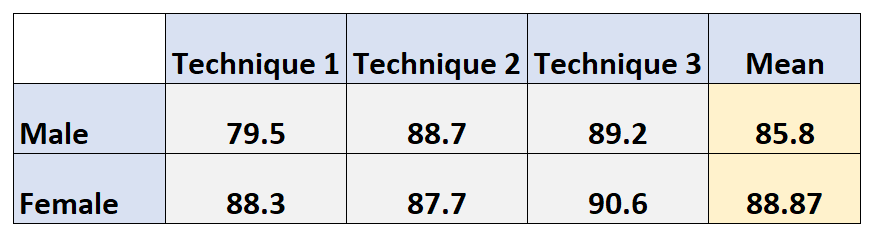
Sarana marjinal teknik belajar hanyalah rata-rata rata-rata setiap tingkat teknik belajar untuk setiap tingkat gender.

Misalnya, nilai ujian rata-rata marjinal siswa yang menggunakan teknik 1 dihitung sebagai berikut:

Rata-rata marjinal teknik 1: (79,5 + 88,3) / 2 = 83,9

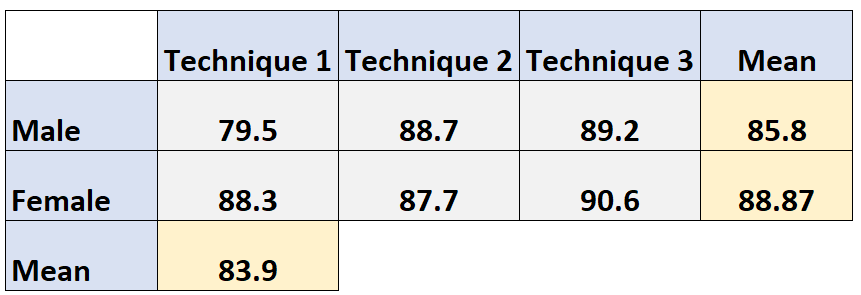
Rata-rata nilai ujian marjinal siswa yang menggunakan teknik 2 dihitung sebagai berikut:

Rata-rata marjinal teknik 2: (88,7 + 87,7) / 2 = 88,2

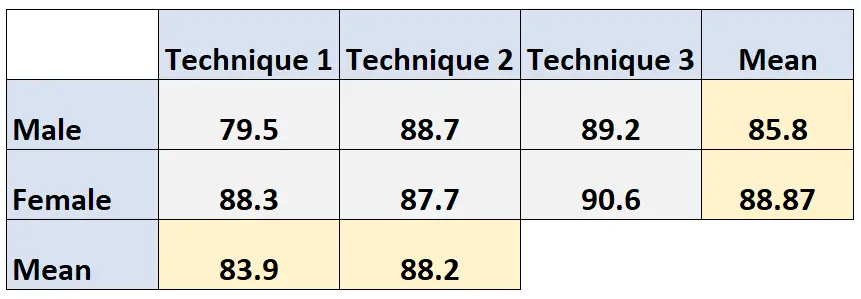
Rata-rata nilai ujian marjinal siswa yang menggunakan teknik 3 dihitung sebagai berikut:

Rata-rata marjinal teknik 3: (89,2 + 90,6) / 2 = 89,9

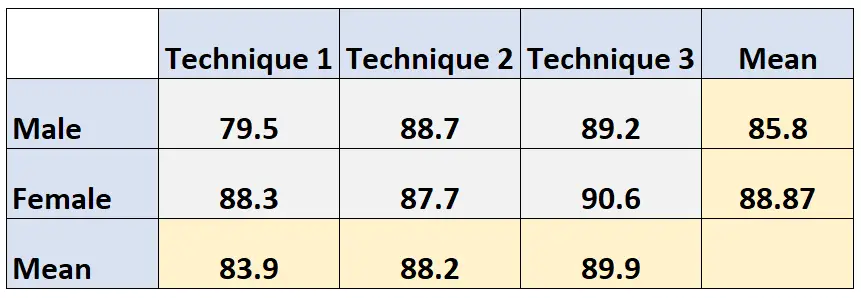
Kita dapat melihat bahwa rata-rata marjinal kedua variabel muncul di margin tabel kontingensi:

Mengapa menggunakan cara-cara marginal?

Rata-rata marjinal berguna karena memberi tahu kita nilai rata-rata keseluruhan untuk tingkat variabel tertentu.

Misalnya, dalam skenario sebelumnya, kita mengetahui hal berikut:

• Rata-rata nilai ujian pria yang menggunakan teknik belajar 1 adalah 79,5.
• Rata-rata nilai ujian pria yang menggunakan teknik belajar 2 adalah 88,7.
• Rata-rata nilai ujian pria yang menggunakan teknik belajar 3 adalah 89,2.

Namun bagaimana jika kita hanya ingin mengetahui skor rata-rata keseluruhan pria?

Rata-rata marjinal laki-laki dapat menjawab hal ini: Skor rata-rata keseluruhan laki-laki adalah 85,8 .

Demikian pula, kami mengetahui hal berikut:

• Rata-rata nilai ujian pria yang menggunakan teknik belajar 1 adalah 79,5.
• Rata-rata nilai ujian wanita yang menggunakan teknik belajar 1 adalah 88,3.

Namun bagaimana jika kita hanya ingin mengetahui nilai rata-rata keseluruhan siswa yang menggunakan teknik belajar 1?

Rata-rata marjinal teknik belajar dapat menjawab sebagai berikut: Nilai rata-rata keseluruhan siswa yang menggunakan teknik belajar 1 adalah 83,9 .

Pada dasarnya, rata-rata marjinal memberi kita cara sederhana untuk memahami rata-rata untuk tingkat variabel tertentu.

Sumber daya tambahan

Apa itu distribusi marjinal?
Apa yang dimaksud dengan distribusi bersama?
Apa itu distribusi bersyarat?