Apa itu tes multinomial? (definisi & #038; contoh)
Uji multinomial digunakan untuk menentukan apakah suatu variabel kategori mengikuti distribusi hipotetis.
Pengujian ini menggunakan hipotesis nol dan hipotesis alternatif berikut:
H 0 : Variabel kategori mengikuti distribusi hipotetis.
H A : Variabel kategori tidak mengikuti distribusi hipotetis.
Jika p-value pengujian berada di bawah tingkat signifikansi tertentu (misalnya α = 0,05), maka kita dapat menolak hipotesis nol dan menyimpulkan bahwa variabel tersebut tidak mengikuti distribusi yang dihipotesiskan.
Tes ini digunakan ketika suatu variabel dapat mengambil k hasil yang berbeda. Contoh klasik dari uji multinomial adalah saat kita ingin menentukan apakah dadu tertentu adil. Ketika sebuah dadu dilempar, peluang munculnya dadu pada setiap angka (1 sampai 6) adalah 1/6.
Untuk menguji apakah sebuah dadu adil, kita dapat melemparnya beberapa kali dan melihat apakah berapa kali dadu tersebut mendarat pada angka yang berbeda berbeda secara signifikan dari yang kita perkirakan.
Contoh berikut menunjukkan cara melakukan pengujian multinomial menggunakan bahasa pemrograman statistik R.
Contoh 1: Dadu Adil
Misalkan kita ingin menentukan apakah sebuah dadu itu adil. Untuk mengujinya, kami menjalankannya 30 kali dan mencatat frekuensi setiap hasil. Tabel berikut menunjukkan hasilnya:
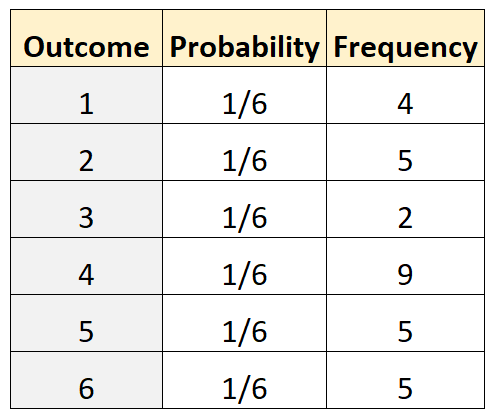
Kode berikut di R dapat digunakan untuk melakukan pengujian multinomial:
library (EMT)
#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)
#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
324632 0 0.4306
Nilai p dari tes ini adalah 0,4306 . Karena nilai p ini tidak kurang dari 0,05, kami tidak akan menolak hipotesis nol. Jadi kita tidak punya cukup bukti untuk mengatakan bahwa dadu itu tidak adil.
Contoh 2: Penjualan produk
Misalkan seorang pemilik toko berhipotesis bahwa jumlah pelanggan yang sama akan membeli empat produk berbeda. Untuk mengujinya, ini mencatat jumlah pelanggan yang membeli setiap produk dalam minggu tertentu. Tabel berikut menunjukkan hasilnya:
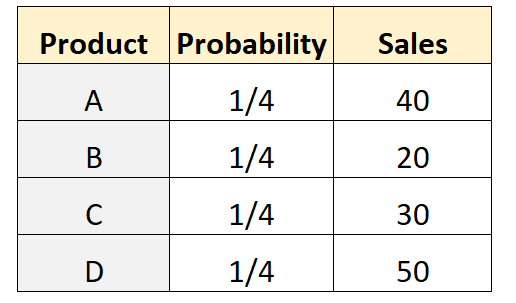
Kode berikut di R dapat digunakan untuk melakukan pengujian multinomial pada kumpulan data ini:
library (EMT)
#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
477191 0 0.00226
Nilai p dari tes ini adalah 0,00226 . Karena nilai p ini kurang dari 0,05, kami akan menolak hipotesis nol. Jadi, kami punya cukup bukti untuk mengatakan bahwa penjualan tidak sama untuk setiap produk.
Contoh 3: Kelereng di dalam tas
Tom menyatakan bahwa peluang terambilnya kelereng merah, hijau, atau ungu dari sebuah kantong berturut-turut adalah 0,2, 0,5, dan 0,3. Untuk mengujinya, temannya Mike merogoh tas dan mengeluarkan kelereng (dengan penggantinya) 100 kali berbeda. Tabel berikut menunjukkan hasilnya:
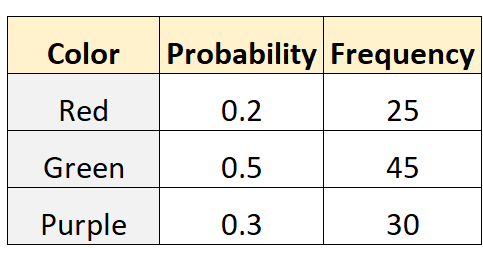
Kode berikut di R dapat digunakan untuk melakukan pengujian multinomial pada kumpulan data ini:
library (EMT)
#specify probability of each outcome
prob <- c(.2, .5, .3)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
5151 0.0037 0.3999
Nilai p dari tes ini adalah 0,3999 . Karena nilai p ini tidak kurang dari 0,05, kita akan gagal menolak hipotesis nol. Oleh karena itu kami tidak mempunyai cukup bukti untuk mengatakan bahwa sebaran kelereng di dalam kantong berbeda dengan yang disebutkan oleh Tom.
Sumber daya tambahan
Pengantar Distribusi Multinomial
Kalkulator Distribusi Multinomial