Cara melakukan tes log rank di r
Tes log-rank adalah cara paling umum untuk membandingkan kurva kelangsungan hidup antara dua kelompok.
Pengujian ini menggunakan asumsi sebagai berikut :
H 0 : Tidak ada perbedaan kelangsungan hidup antara kedua kelompok.
H A : Terdapat perbedaan survival antara kedua kelompok.
Jika p-value uji berada di bawah tingkat signifikansi tertentu (misalnya α = 0,05), maka kita dapat menolak hipotesis nol dan menyimpulkan bahwa terdapat cukup bukti yang mengatakan bahwa terdapat perbedaan kelangsungan hidup antara kedua kelompok.
Untuk melakukan pengujian log-rank di R, kita dapat menggunakan fungsi survdiff() dari paket survival , yang menggunakan sintaks berikut:
survdiff(Surv(waktu, status) ~ prediktor, data)
Fungsi ini mengembalikan statistik uji chi-kuadrat dan nilai p yang sesuai.
Contoh berikut menunjukkan cara menggunakan fungsi ini untuk melakukan pengujian log-rank di R.
Contoh: Tes Log Rank di R
Untuk contoh ini, kita akan menggunakan dataset ovarium dari paket survival . Kumpulan data ini berisi informasi berikut pada 26 pasien:
- Waktu bertahan hidup (dalam bulan) setelah didiagnosis menderita kanker ovarium
- Apakah waktu bertahan hidup disensor atau tidak
- Jenis pengobatan yang diterima (rx = 1 atau rx = 2)
Kode berikut menunjukkan cara menampilkan enam baris pertama kumpulan data ini:
library (survival) #view first six rows of dataset head(ovarian) futime fustat age resid.ds rx ecog.ps 1 59 1 72.3315 2 1 1 2 115 1 74.4932 2 1 1 3 156 1 66.4658 2 1 2 4 421 0 53.3644 2 2 1 5,431 1 50.3397 2 1 1 6 448 0 56.4301 1 1 2
Kode berikut menunjukkan cara melakukan uji log-rank untuk menentukan apakah ada perbedaan kelangsungan hidup antara pasien yang menerima perawatan berbeda:
#perform log rank test
survdiff(Surv(futime, fustat) ~ rx, data=ovarian)
Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)
N Observed Expected (OE)^2/E (OE)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06
Chisq= 1.1 on 1 degrees of freedom, p= 0.3
Statistik uji Chi-kuadrat adalah 1,1 dengan 1 derajat kebebasan dan nilai p yang sesuai adalah 0,3 . Karena nilai p ini tidak kurang dari 0,05, kita gagal menolak hipotesis nol.
Dengan kata lain, kami tidak memiliki cukup bukti untuk mengatakan bahwa terdapat perbedaan yang signifikan secara statistik dalam kelangsungan hidup antara kedua pengobatan tersebut.
Kita juga dapat memplot kurva kelangsungan hidup untuk setiap kelompok menggunakan sintaks berikut:
#plot survival curves for each treatment group plot(survfit(Surv(futime, fustat) ~ rx, data = ovarian), xlab = " Time ", ylab = “ Overall survival probability ”)
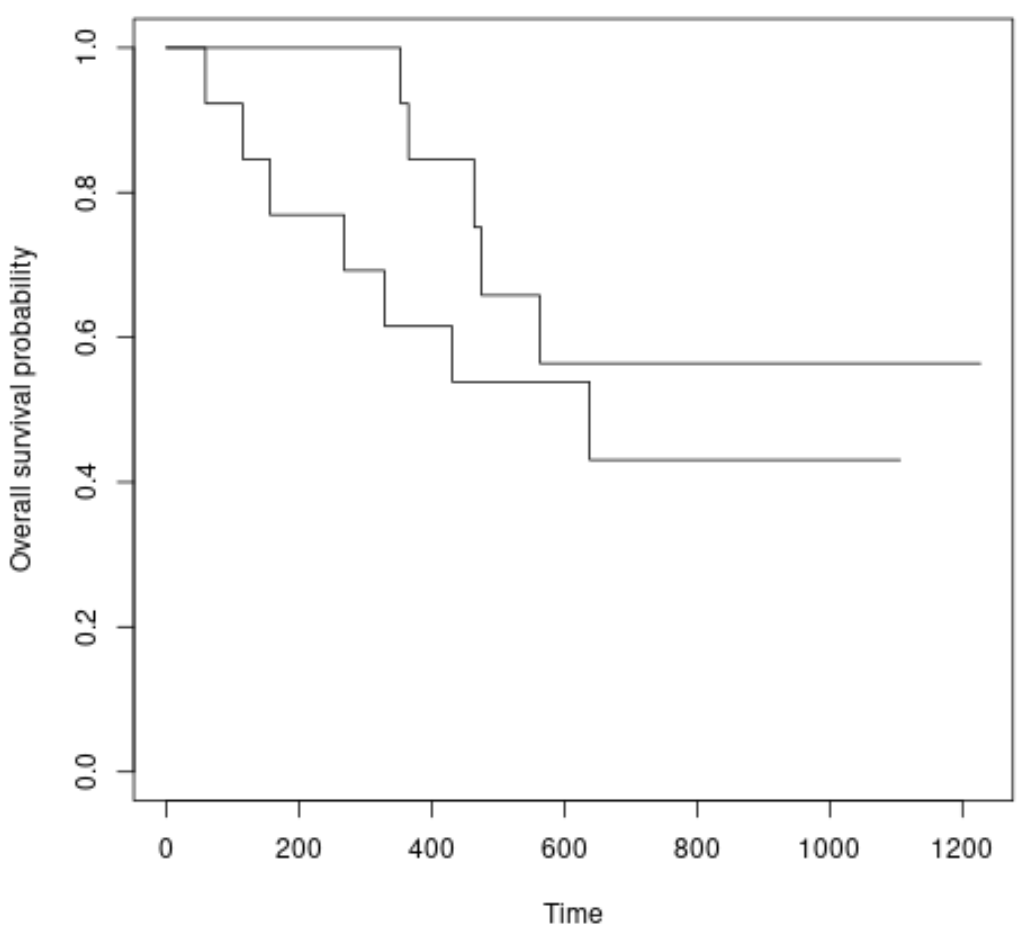
Kita dapat melihat bahwa kurva kelangsungan hidup sedikit berbeda, namun uji log-rank menunjukkan bahwa perbedaan tersebut tidak signifikan secara statistik.