Apa itu regresi lengkung? (definisi & contoh)
Regresi lengkung adalah nama yang diberikan untuk model regresi apa pun yang berupaya menyesuaikan kurva , bukan garis lurus.
Contoh umum model regresi lengkung meliputi:
Regresi kuadrat: digunakan ketika terdapat hubungan kuadrat antara variabel prediktor dan variabel respons . Jika dibuat grafiknya, jenis hubungan ini terlihat seperti huruf “U” atau “U” terbalik pada diagram sebar:
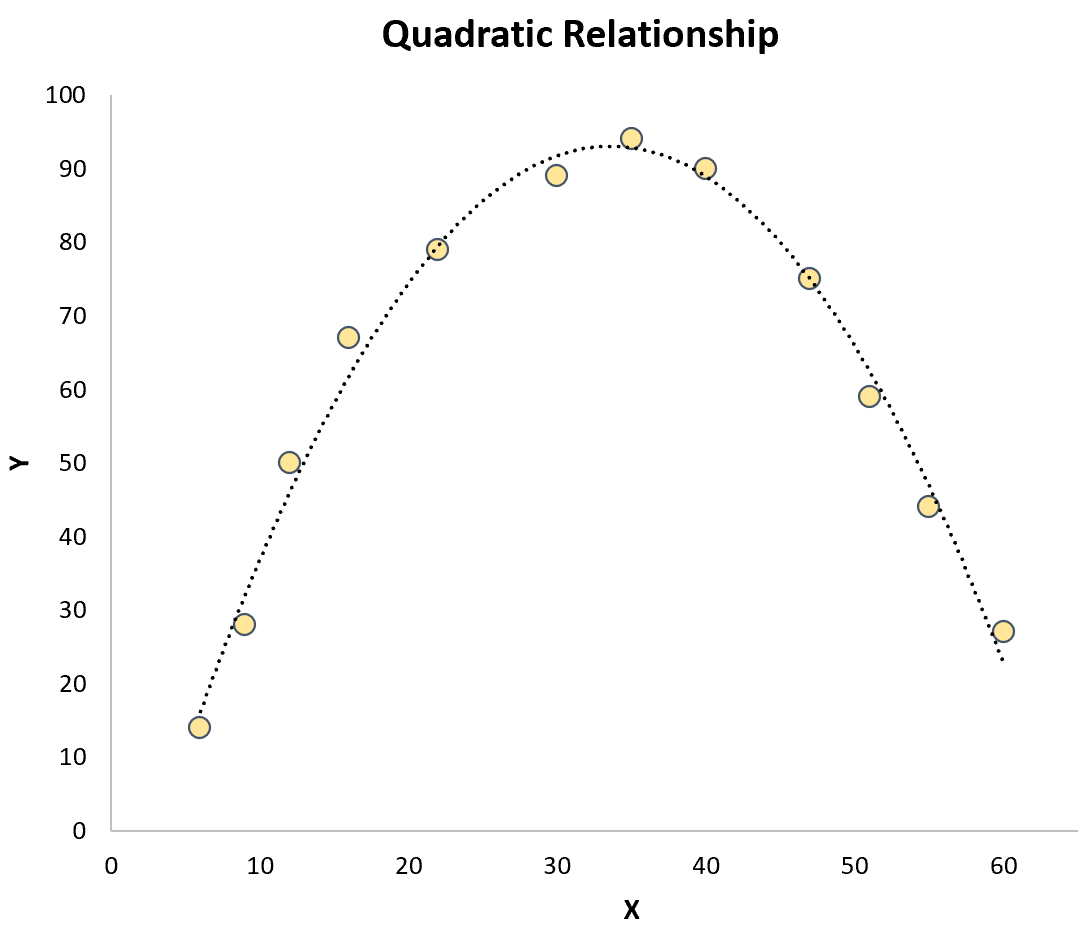
Regresi Kubik: Digunakan ketika ada hubungan kubik antara variabel prediktor dan variabel respons. Jika dibuat grafiknya, jenis hubungan ini menunjukkan dua kurva berbeda pada plot sebar:
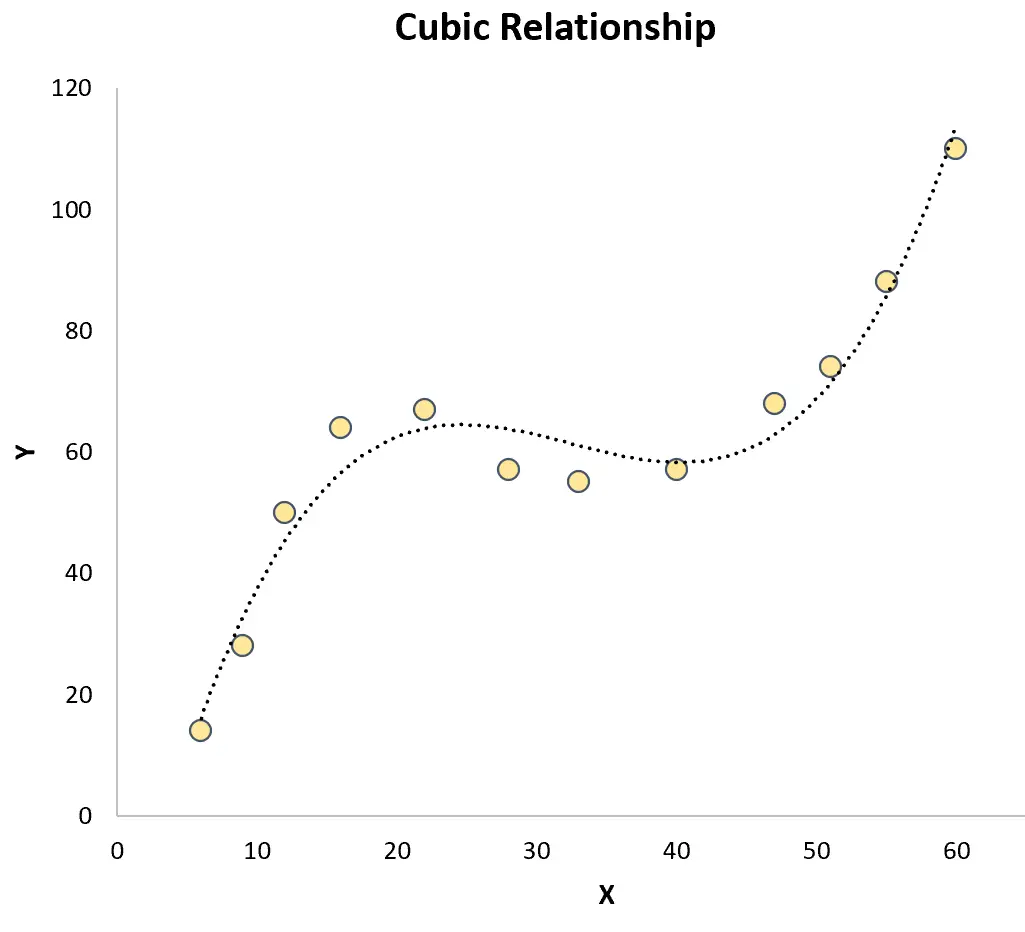
Keduanya berbeda dengan regresi linier sederhana yang hubungan antara variabel prediktor dan variabel respon adalah linier:
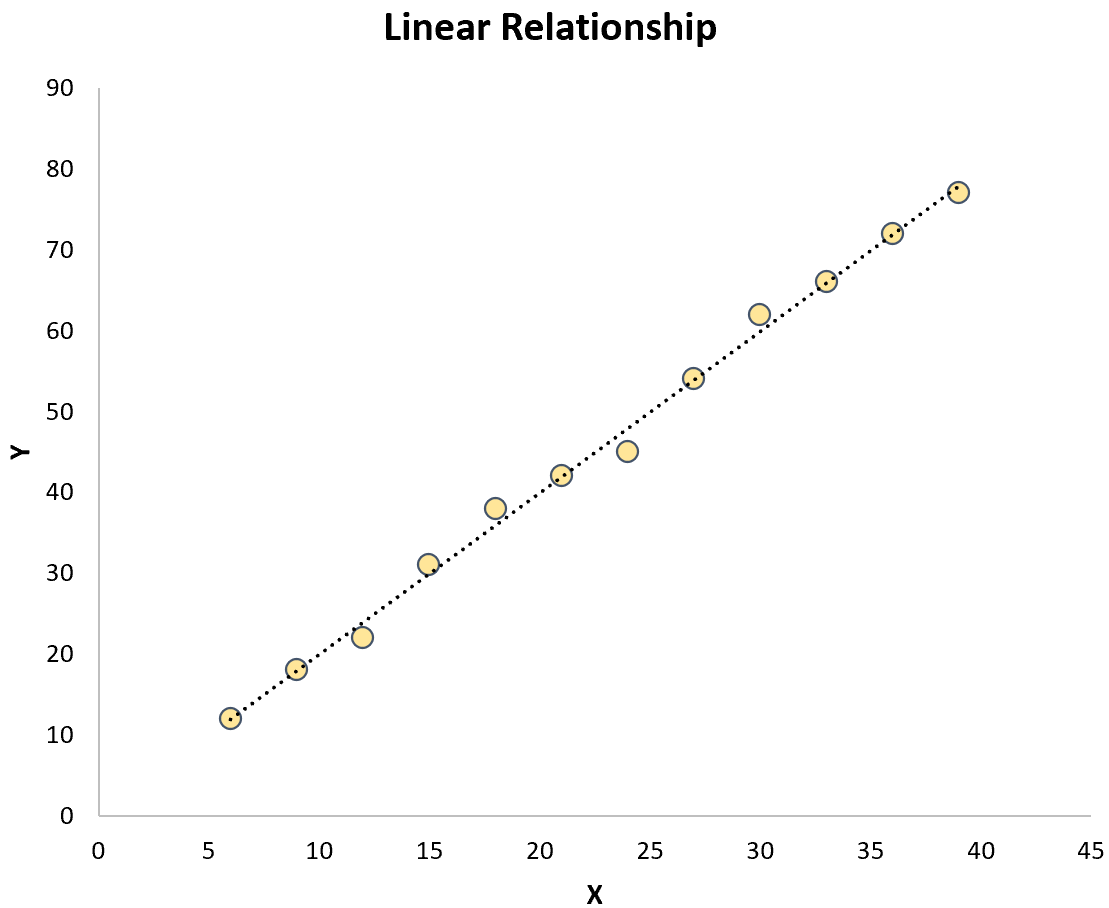
Rumus model regresi lengkung
Model regresi linier sederhana mencoba menyesuaikan sekumpulan data menggunakan rumus berikut:
ŷ = β 0 + β 1 x
Emas:
- ŷ : Variabel respon
- β 0 , β 1 : Koefisien regresi
- x: variabel prediktif
Sebaliknya, model regresi kuadrat menggunakan rumus berikut:
ŷ = β 0 + β 1 x + β 2 x 2
Dan model regresi kubik menggunakan rumus sebagai berikut:
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
Nama yang lebih umum untuk model regresi yang menyertakan eksponen adalah regresi polinomial , yang menggunakan rumus berikut:
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
Nilai k menunjukkan derajat polinomial. Meskipun derajatnya bisa berupa angka positif apa pun, dalam praktiknya kita jarang menggunakan model regresi polinomial dengan derajat lebih besar dari 3 atau 4.
Dengan menggunakan eksponen dalam rumus model regresi, model regresi polinomial dapat menyesuaikan kurva dengan kumpulan data, bukan garis lurus.
Kapan menggunakan regresi lengkung
Cara termudah untuk mengetahui apakah Anda harus menggunakan regresi lengkung atau tidak adalah dengan membuat plot sebar dari variabel prediktor dan variabel respon.
Jika diagram sebar menunjukkan hubungan linier antara kedua variabel, regresi linier sederhana mungkin lebih tepat.
Namun jika scatterplot menunjukkan pola kuadrat, kubik, atau pola lengkung lainnya antara prediktor dan variabel respon, maka regresi lengkung mungkin lebih tepat digunakan.
Anda juga dapat menyesuaikan model regresi linier sederhana dan model regresi lengkung dan membandingkan nilai R-kuadrat yang dipasang dari setiap model untuk menentukan model mana yang paling sesuai dengan data.
R-squared yang disesuaikan berguna karena menunjukkan seberapa besar varians dalam variabel respons yang dapat dijelaskan oleh variabel prediktor, disesuaikan dengan jumlah variabel prediktor dalam model.
Secara umum, model dengan nilai R-kuadrat penyesuaian tertinggi memberikan kesesuaian yang lebih baik dengan kumpulan data.
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan regresi polinomial dalam perangkat lunak statistik yang berbeda:
Pengantar Regresi Polinomial
Cara Melakukan Regresi Polinomial di Excel
Cara melakukan regresi polinomial dengan Python
Bagaimana melakukan regresi polinomial di R
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya