Cara melakukan regresi yang kuat di r (langkah demi langkah)

Regresi Robust adalah metode yang dapat kita gunakan sebagai alternatif dari regresi kuadrat terkecil biasa ketika terdapat outlier atau observasi yang berpengaruh pada dataset yang kita kerjakan.

Untuk melakukan regresi yang kuat di R, kita dapat menggunakan fungsi rlm() dari paket MASS , yang menggunakan sintaks berikut:

Contoh langkah demi langkah berikut menunjukkan cara melakukan regresi yang kuat di R untuk kumpulan data tertentu.

Langkah 1: Buat datanya

Pertama, mari buat kumpulan data palsu untuk digunakan:

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

Langkah 2: Lakukan Regresi Kuadrat Terkecil Biasa

Selanjutnya, mari kita sesuaikan model regresi kuadrat terkecil biasa dan buat plot dari residu terstandardisasi .

Dalam praktiknya, kita sering menganggap residu terstandar yang nilai absolutnya lebih besar dari 3 sebagai outlier.

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

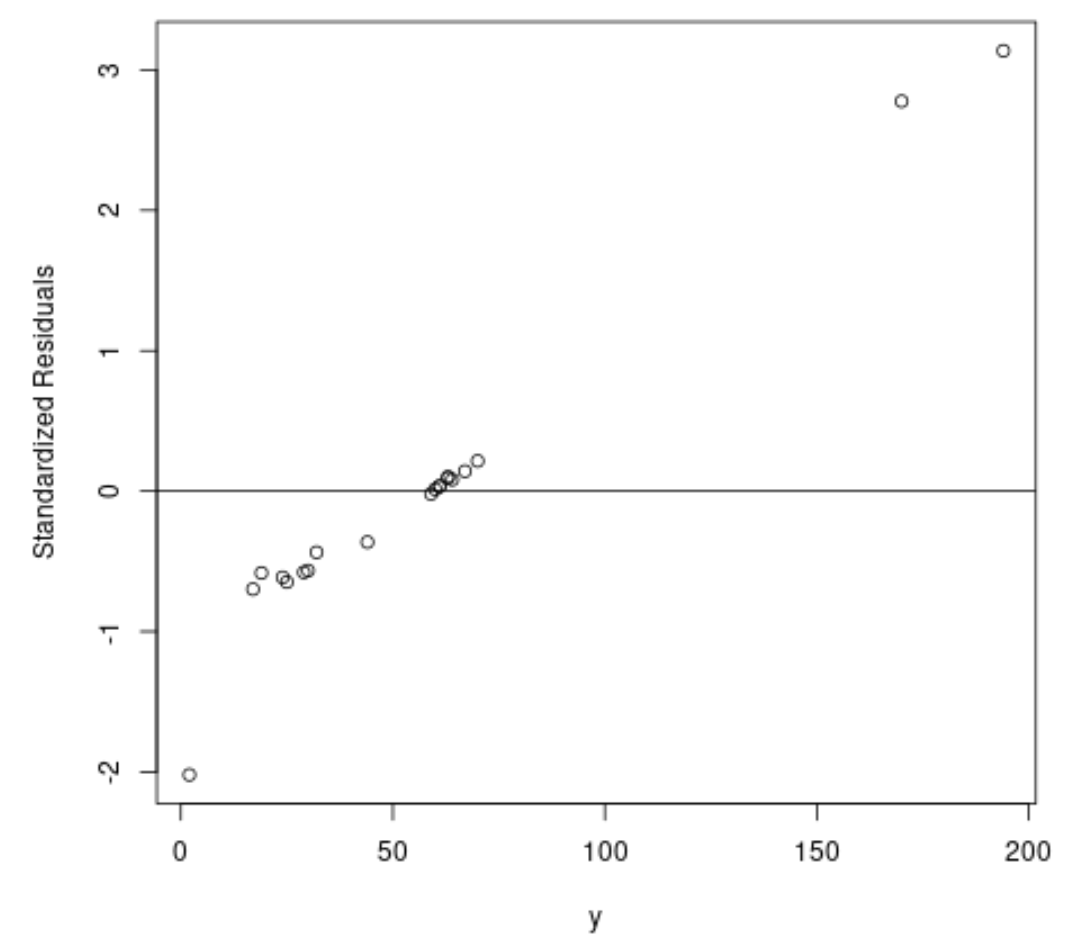
Dari grafik terlihat terdapat dua observasi dengan residu terstandar sekitar 3.

Hal ini menunjukkan bahwa ada dua potensi outlier dalam kumpulan data dan oleh karena itu kita mungkin mendapat manfaat dari regresi yang kuat.

Langkah 3: Lakukan Regresi yang Kuat

Selanjutnya, mari kita gunakan fungsi rlm() agar sesuai dengan model regresi yang kuat:

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

Untuk menentukan apakah model regresi kuat ini memberikan kesesuaian data yang lebih baik dibandingkan dengan model OLS, kita dapat menghitung kesalahan standar sisa dari setiap model.

Kesalahan standar sisa (RSE) adalah cara untuk mengukur simpangan baku dari sisa dalam model regresi. Semakin rendah nilai CSR, semakin baik suatu model mampu menyesuaikan dengan data.

Kode berikut menunjukkan cara menghitung RSE untuk setiap model:

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

Kita dapat melihat bahwa RSE dari model regresi yang kuat jauh lebih rendah dibandingkan dengan model regresi kuadrat terkecil biasa, yang menunjukkan bahwa model regresi yang kuat memberikan kesesuaian yang lebih baik dengan data.

Sumber daya tambahan

Cara melakukan regresi linier sederhana di R
Cara melakukan regresi linier berganda di R
Bagaimana melakukan regresi polinomial di R