Perbedaan fisher yang paling tidak signifikan: definisi + contoh

ANOVA satu arah digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga atau lebih kelompok independen.

Asumsi yang digunakan dalam ANOVA adalah sebagai berikut:

H ₀ : Rata-ratanya sama untuk setiap kelompok.

H _A : Setidaknya salah satu caranya berbeda dengan yang lain.

Jika nilai p dari ANOVA berada di bawah tingkat signifikansi tertentu (seperti α = 0,05), kita dapat menolak hipotesis nol dan menyimpulkan bahwa setidaknya salah satu mean kelompok berbeda dari mean kelompok lainnya.

Namun untuk mengetahui secara pasti kelompok mana yang berbeda satu sama lain, kita perlu melakukan tes post-hoc.

Uji post hoc yang umum digunakan adalah uji beda signifikan terkecil Fisher .

Untuk melakukan pengujian ini, pertama-tama kita menghitung statistik pengujian berikut:

LSD = t _0,025 , _{DF w} * √ MS _W (1/n ₁ + 1/n ₁ )

Emas:

• t _0,025 , _DFw : Nilai t-kritis dari tabel distribusi t dengan α = 0,025 dan DF _w sesuai dengan derajat kebebasan dalam kelompok tabel ANOVA.
• MS _W : Rata-rata kuadrat dalam kelompok dalam tabel ANOVA.
• n ₁ , n ₂ : Ukuran sampel setiap kelompok

Kami kemudian dapat membandingkan perbedaan rata-rata antara masing-masing kelompok dengan statistik pengujian ini. Jika nilai absolut dari perbedaan rata-rata antara dua kelompok lebih besar dari statistik uji, kita dapat menyatakan bahwa terdapat perbedaan yang signifikan secara statistik antara rata-rata kelompok.

Contoh berikut menunjukkan cara melakukan uji perbedaan signifikan terkecil Fisher dalam praktiknya.

Contoh: Uji Beda Signifikansi Terkecil Fisher

Misalkan seorang profesor ingin mengetahui apakah tiga teknik belajar yang berbeda menghasilkan nilai ujian yang berbeda di kalangan siswa. Untuk mengujinya, dia secara acak menugaskan 10 siswa untuk menggunakan setiap teknik belajar dan mencatat hasil ujian mereka.

Berikut tabel hasil ujian masing-masing siswa berdasarkan teknik belajar yang digunakan:

Profesor melakukan ANOVA satu arah dan memperoleh hasil sebagai berikut:

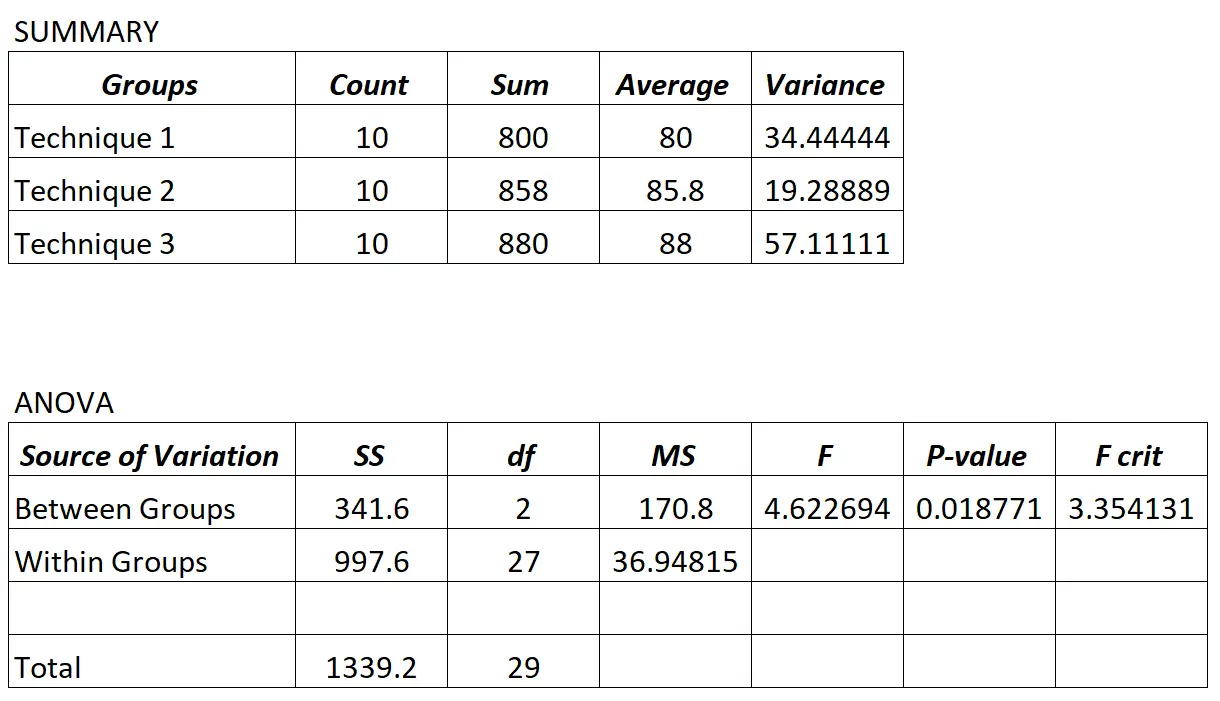
Karena nilai p pada tabel ANOVA (0,018771) kurang dari 0,05, maka kita dapat menyimpulkan bahwa semua rata-rata nilai ujian antara ketiga kelompok tidak sama.

Jadi, kita dapat melakukan uji beda signifikan terkecil Fisher untuk menentukan mean kelompok mana yang berbeda.

Dengan menggunakan nilai hasil ANOVA, kita dapat menghitung statistik uji Fisher sebagai berikut:

• LSD = t _0,025 , _DFw * √ MS _W (1/n ₁ + 1/n ₁ )
• LSD = t _0,025 , ₂₇ * √ 36,948*(1/10 + 1/10)
• LSD = 2,052* √7,3896
• LSD = 5,578

Kami kemudian dapat menghitung perbedaan rata-rata absolut antara masing-masing kelompok:

• Teknik 1 versus Teknik 2: |80 – 85,8| = 5.8
• Teknik 1 versus Teknik 3: |80 – 88| = 8
• Teknik 2 versus Teknik 3: |85.8 – 88| = 2.2

Perbedaan rata-rata absolut antara teknik 1 dan teknik 2 dan antara teknik 1 dan teknik 3 lebih besar dibandingkan statistik uji Fisher. Oleh karena itu, kami dapat menyimpulkan bahwa teknik ini menghasilkan nilai ujian rata-rata yang berbeda secara signifikan secara statistik.

Dapat juga disimpulkan bahwa tidak terdapat perbedaan rata-rata nilai ujian yang signifikan antara teknik 2 dan teknik 3.