Cara melakukan tes f parsial di excel
Uji F parsial digunakan untuk menentukan ada atau tidaknya perbedaan yang signifikan secara statistik antara model regresi dan versi tersarang dari model yang sama.
Model bersarang hanyalah model yang berisi subkumpulan variabel prediktor dalam model regresi keseluruhan.
Misalnya, kita memiliki model regresi berikut dengan empat variabel prediktor:
Y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4 + ε
Contoh model bertingkat adalah model berikut yang hanya memiliki dua variabel prediktor asli:
Y = β 0 + β 1 x 1 + β 2 x 2 + ε
Untuk mengetahui apakah kedua model ini berbeda secara signifikan, kita dapat melakukan uji F parsial, yang menghitung statistik uji F berikut:
F = (( RSS yang Dikurangi – RSS Penuh )/p) / ( RSS Penuh /nk)
Emas:
- RSS yang Dikurangi : Jumlah sisa kuadrat dari model yang dikurangi (yaitu “bersarang”).
- RSS penuh : Jumlah sisa kuadrat dari model lengkap.
- p : jumlah prediktor yang dihapus dari model lengkap.
- n: jumlah total observasi dalam kumpulan data.
- k : Jumlah koefisien (termasuk intersep) dalam model lengkap.
Pengujian ini menggunakan hipotesis nol dan hipotesis alternatif berikut:
H 0 : Semua koefisien yang dihilangkan dari model penuh adalah nol.
H A : Setidaknya salah satu koefisien yang dikeluarkan dari model lengkap adalah bukan nol.
Jika nilai p yang sesuai dengan statistik uji F berada di bawah tingkat signifikansi tertentu (misalnya 0,05), maka kita dapat menolak hipotesis nol dan menyimpulkan bahwa setidaknya salah satu koefisien yang dikeluarkan dari model lengkap adalah signifikan.
Contoh berikut memperlihatkan cara melakukan uji F parsial di Excel.
Contoh: uji F parsial di Excel
Misalkan kita memiliki kumpulan data berikut di Excel:
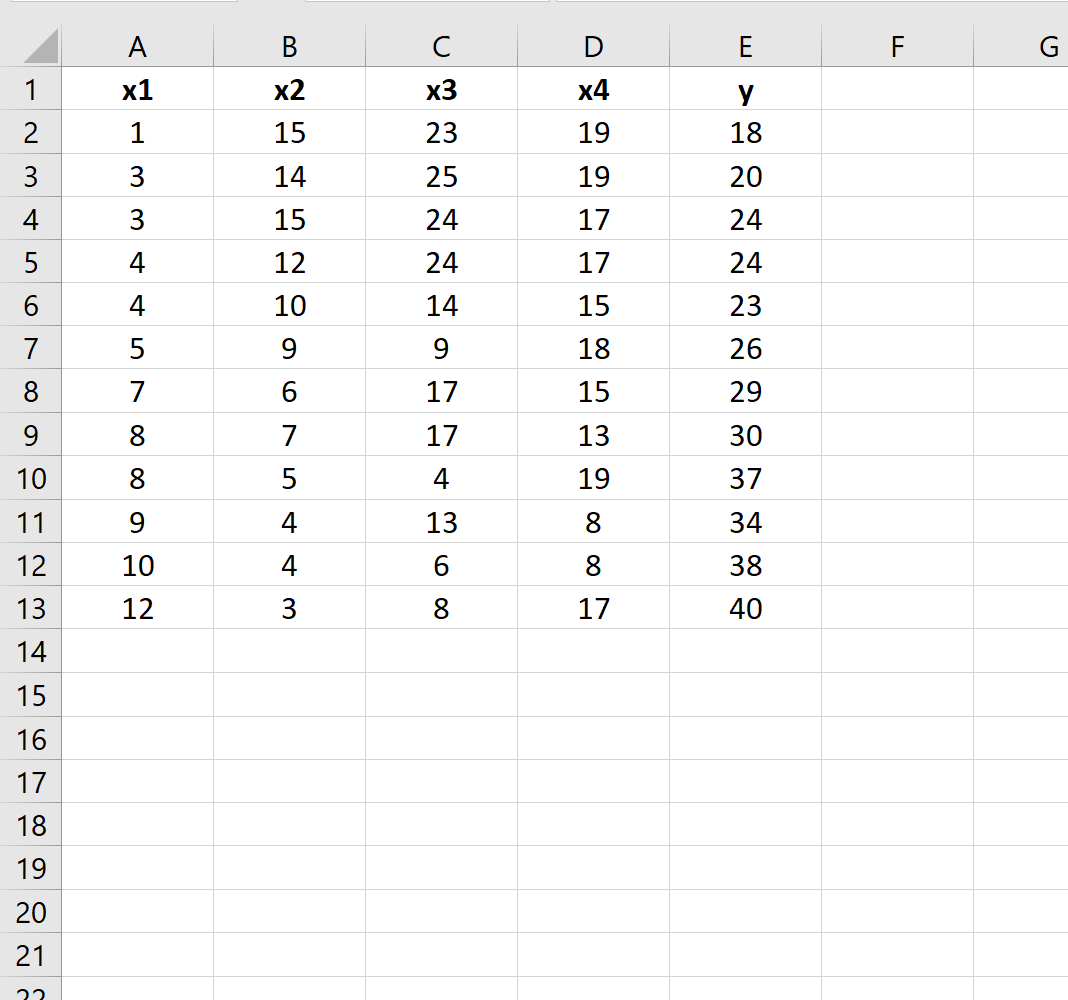
Misalkan kita ingin mengetahui apakah terdapat perbedaan antara dua model regresi berikut:
Model lengkap: y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
Model tereduksi: y = β 0 + β 1 x 1 + β 2 x 2
Kita dapat melakukan regresi linier berganda di Excel untuk setiap model untuk mendapatkan hasil sebagai berikut:
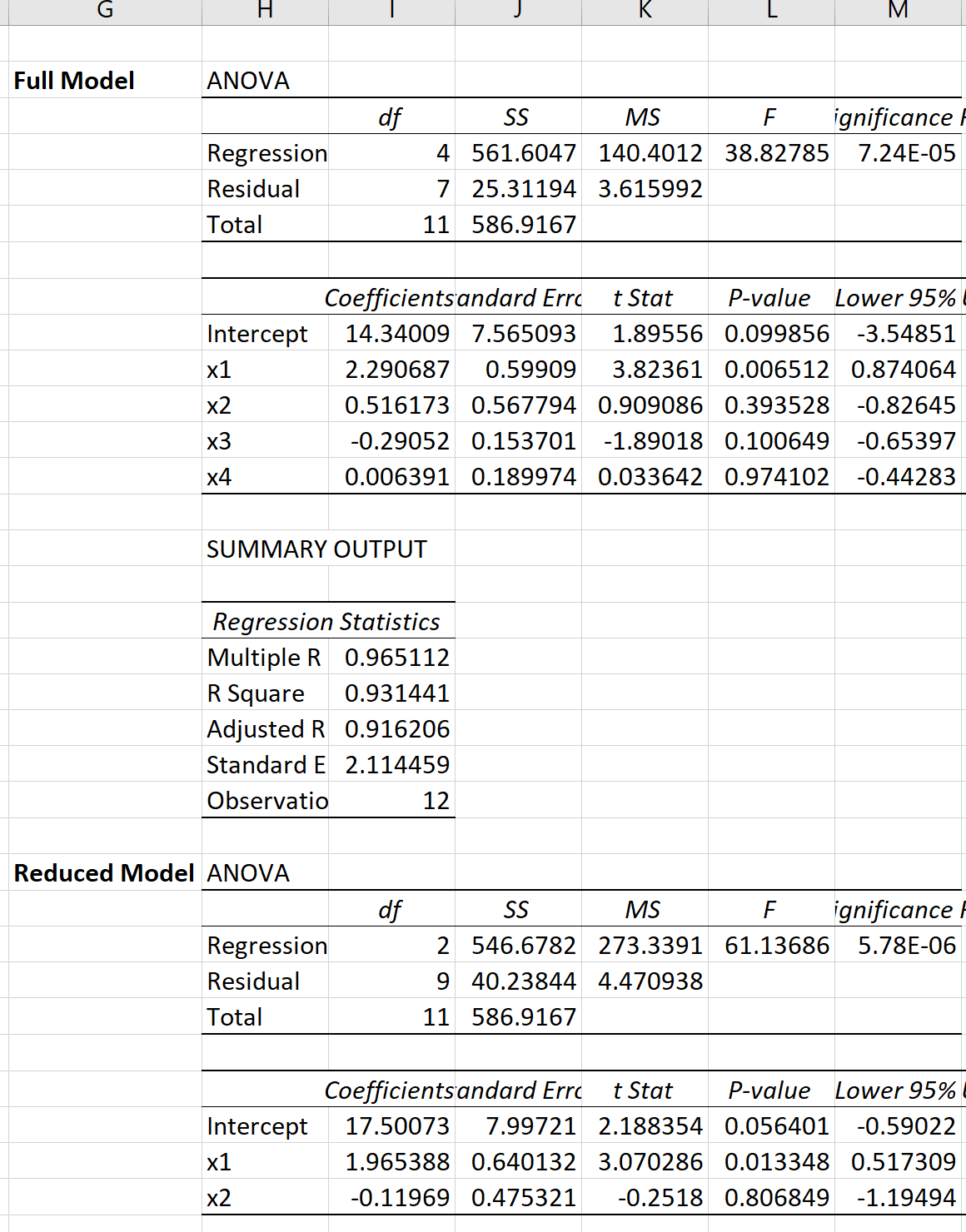
Kita kemudian dapat menggunakan rumus berikut untuk menghitung statistik uji F untuk uji F parsial:
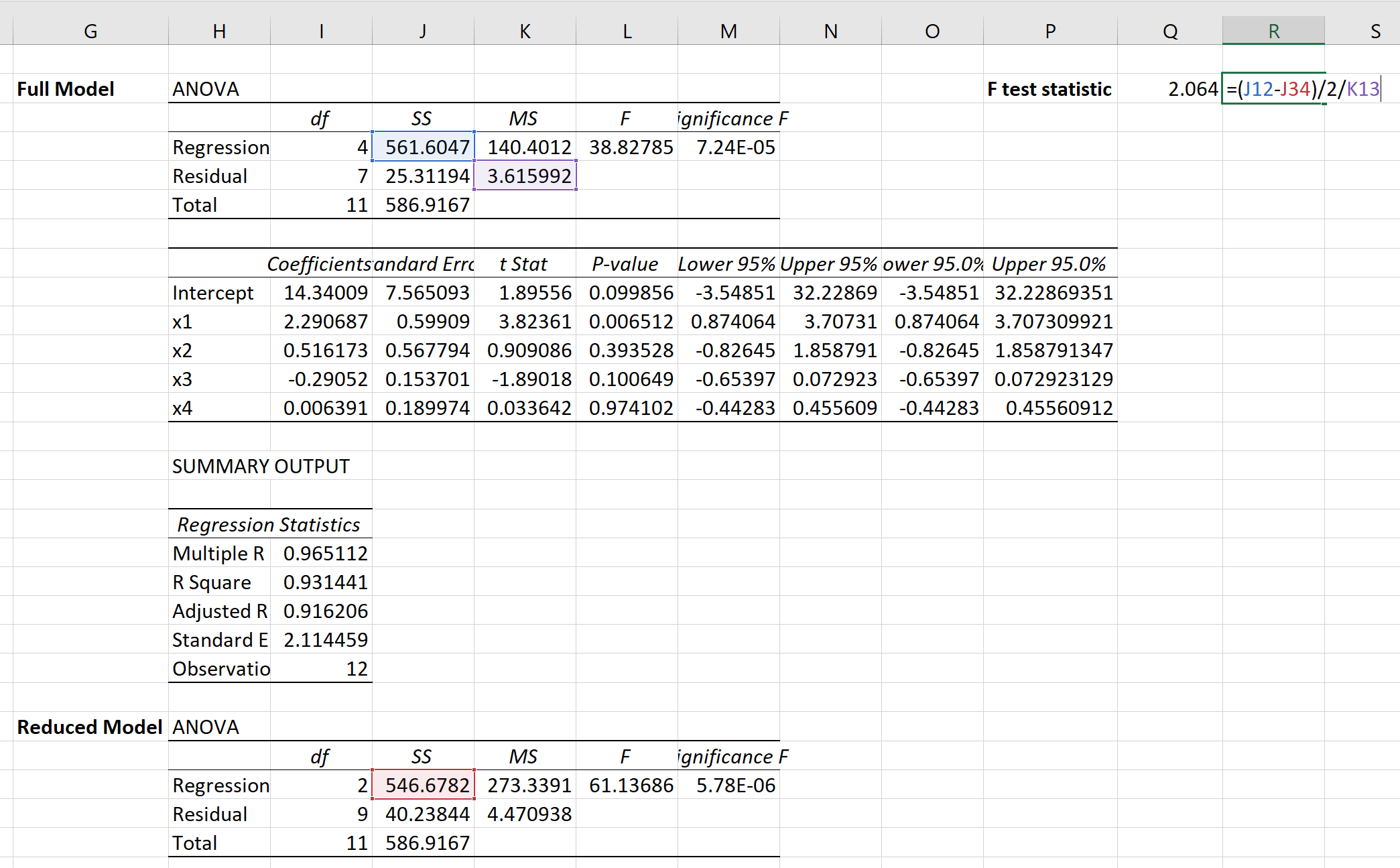
Statistik pengujiannya ternyata 2.064 .
Kita kemudian dapat menggunakan rumus berikut untuk menghitung nilai p yang sesuai:
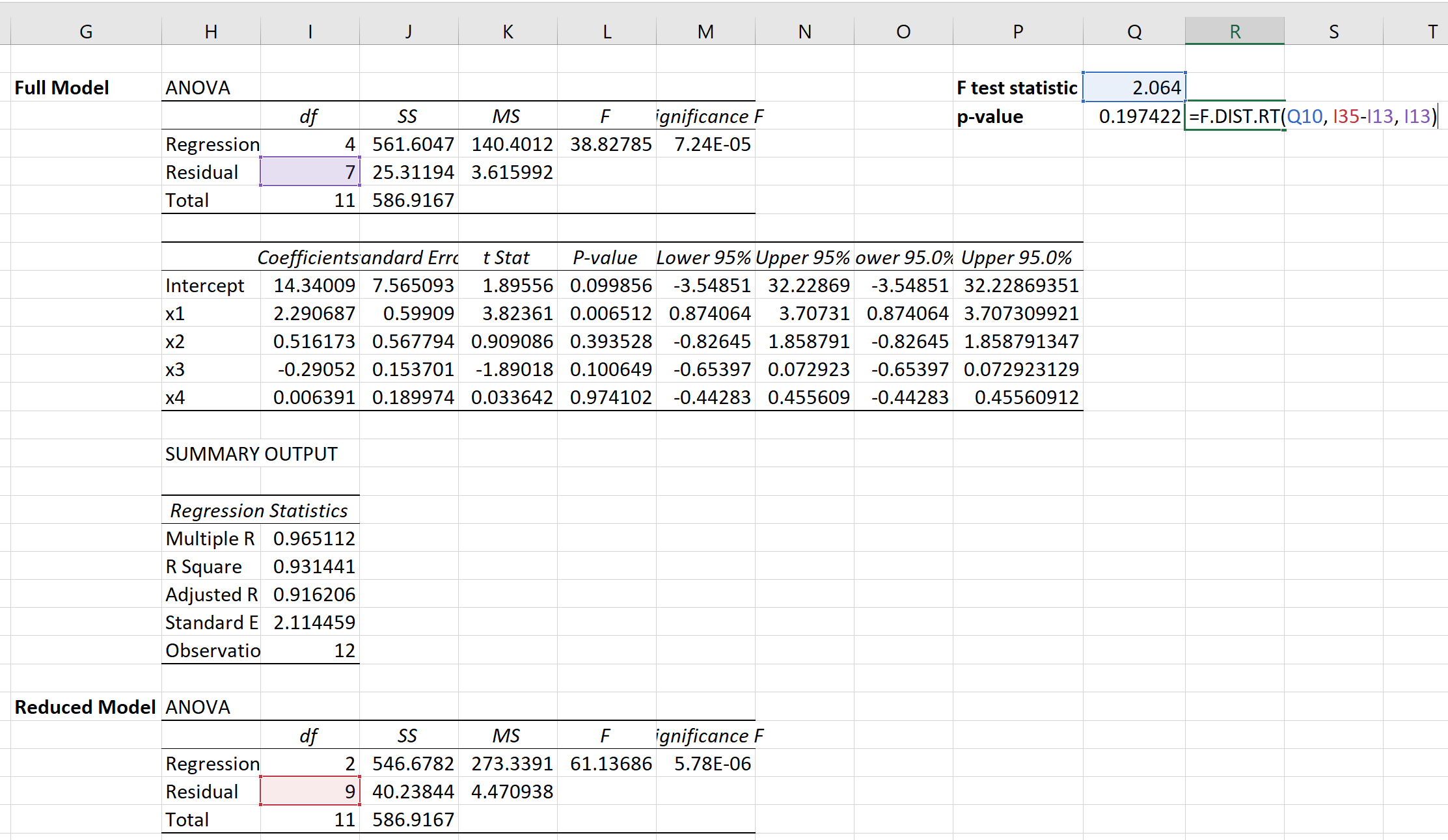
Nilai pnya ternyata 0,1974 .
Karena nilai p ini tidak kurang dari 0,05, kita akan gagal menolak hipotesis nol. Artinya kita tidak mempunyai cukup bukti untuk menyatakan bahwa salah satu variabel prediktor x3 atau x4 signifikan secara statistik.
Dengan kata lain, menambahkan x3 dan x4 ke model regresi tidak meningkatkan kecocokan model secara signifikan.
Sumber daya tambahan
Cara melakukan regresi linier sederhana di Excel
Cara melakukan regresi linier berganda di Excel
Cara Menghitung Standard Error Regresi di Excel
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya