Distribusi normal dan distribusi normal standar: perbedaannya

Distribusi normal adalah distribusi probabilitas yang paling umum digunakan dalam statistik.

Ini memiliki properti berikut:

• Simetris
• Berbentuk lonceng
• Rata-rata dan mediannya sama; keduanya terletak di pusat distribusi

Rata-rata distribusi normal menentukan lokasinya dan simpangan baku menentukan penyebarannya.

Misalnya, grafik berikut menunjukkan tiga distribusi normal dengan mean dan deviasi standar yang berbeda:

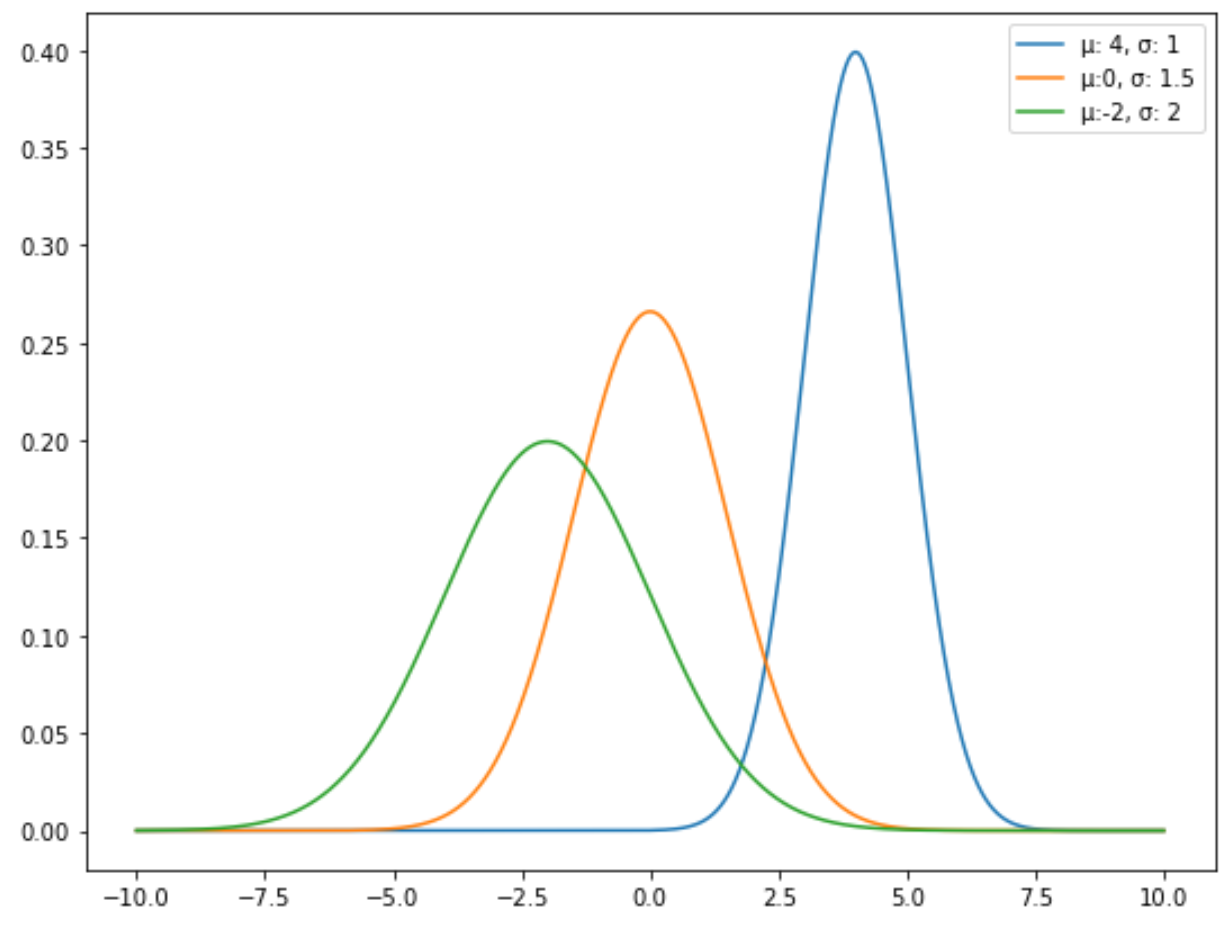
Distribusi normal baku adalah jenis distribusi normal tertentu yang meannya adalah 0 dan simpangan bakunya adalah 1.

Grafik berikut menunjukkan distribusi normal standar:

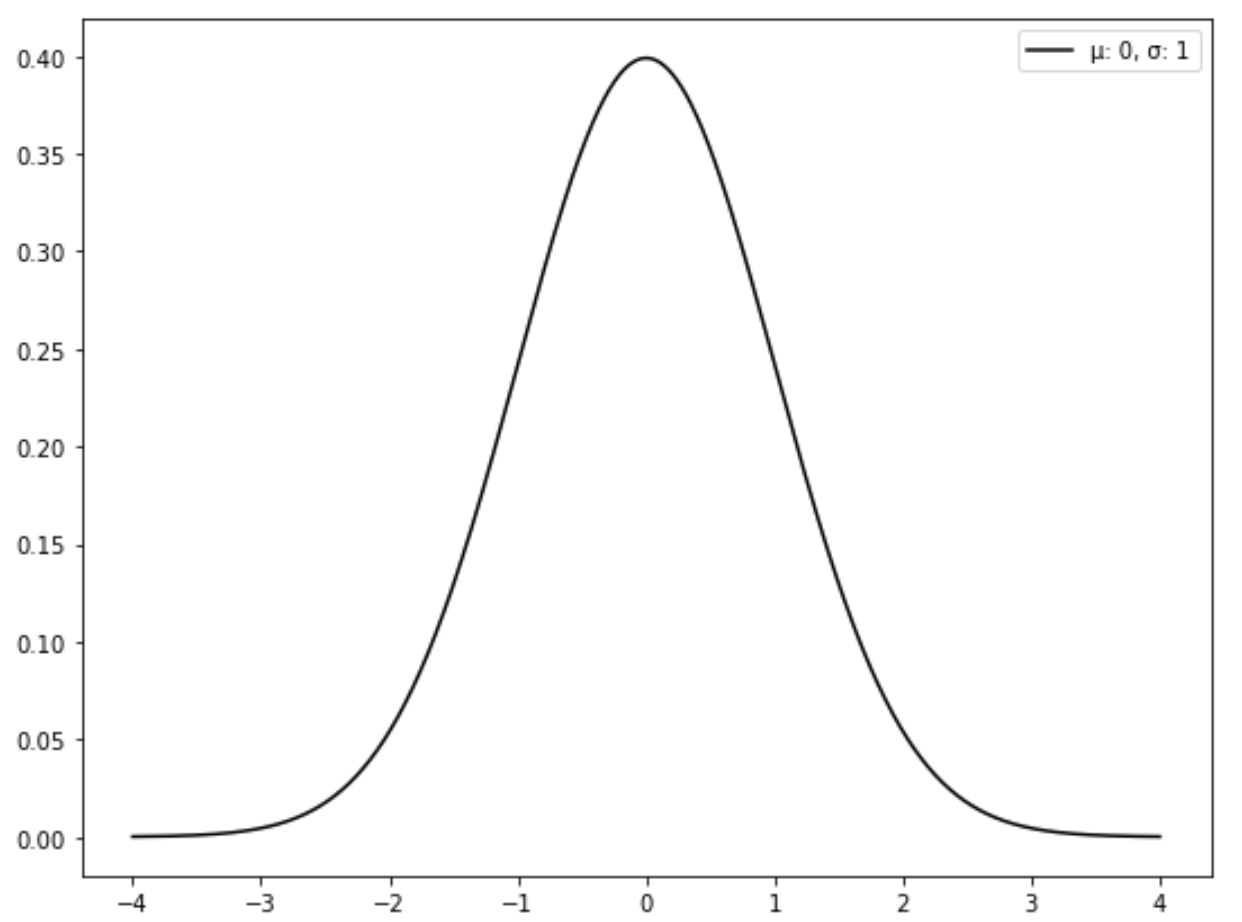
Cara mengubah distribusi normal menjadi distribusi normal standar

Distribusi normal apa pun dapat diubah menjadi distribusi normal standar dengan mengubah nilai data menjadi skor-z, menggunakan rumus berikut:

z = (x – μ) / σ

Emas:

• x: nilai data individu
• μ: Rata-rata distribusi
• σ : Simpangan baku distribusi

Misalnya, kita mempunyai kumpulan data berikut dengan rata-rata 6 dan deviasi standar 2,152:

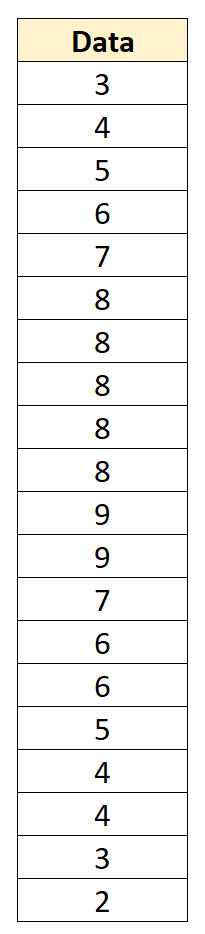
Kita dapat mengonversi setiap nilai data menjadi skor-z dengan mengurangkan 6 dari setiap nilai dan membaginya dengan 2,152:

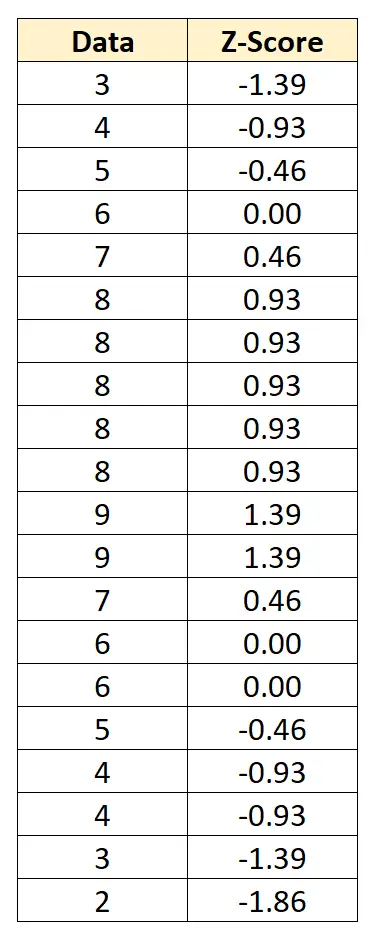
Skor-z memberi tahu kita berapa banyak standar deviasi setiap titik data dari mean. Misalnya, nilai data pertama “3” adalah 1,39 standar deviasi di bawah rata-rata.

Rata-rata distribusi skor ini mempunyai rata-rata nol dan simpangan baku satu.

Cara menggunakan distribusi normal standar

Distribusi normal standar mempunyai sifat-sifat sebagai berikut:

• Sekitar 68% data berada dalam satu standar deviasi mean
• Sekitar 95% data berada dalam dua standar deviasi dari mean.
• Sekitar 99,7% data berada dalam tiga standar deviasi mean.

Ini dikenal sebagai aturan praktis dan digunakan untuk memahami distribusi nilai dalam kumpulan data.

Misalnya, tinggi tanaman di suatu taman berdistribusi normal dengan rata-rata 47,4 inci dan simpangan baku 2,4 inci.

Dengan menggunakan aturan praktis, berapa persentase tanaman yang tingginya kurang dari 54,6 inci?

Aturan praktisnya menyatakan bahwa untuk kumpulan data tertentu dengan distribusi normal, 99,7% nilai data berada dalam tiga standar deviasi mean. Artinya, 49,85% nilainya berada di antara mean dan tiga standar deviasi di atas mean.

Dalam contoh ini, 54,6 adalah tiga standar deviasi di atas rata-rata. Karena kita mengetahui bahwa 50% nilai datanya lebih kecil dari mean pada distribusi normal, maka total 50% + 49,85% = 99,85% nilainya kurang dari 54,6.

Jadi 99,85% tanaman tingginya kurang dari 54,6 inci.

Sumber daya tambahan

Masalah dalam mempraktikkan aturan praktis
Aturan Kalkulator Jempol
Bagaimana menerapkan aturan praktis di Excel