Cara menemukan skor z di area tertentu (dengan contoh)
Ada tiga cara untuk mencari skor-z yang sesuai dengan area tertentu di bawah kurva distribusi normal
1. Gunakan tabel z.
2. Gunakan kalkulator persentil skor Z.
3. Gunakan fungsi invNorm() pada kalkulator TI-84 .
Contoh berikut menunjukkan cara menggunakan masing-masing metode ini untuk mencari skor-z yang sesuai dengan area tertentu di bawah kurva distribusi normal.
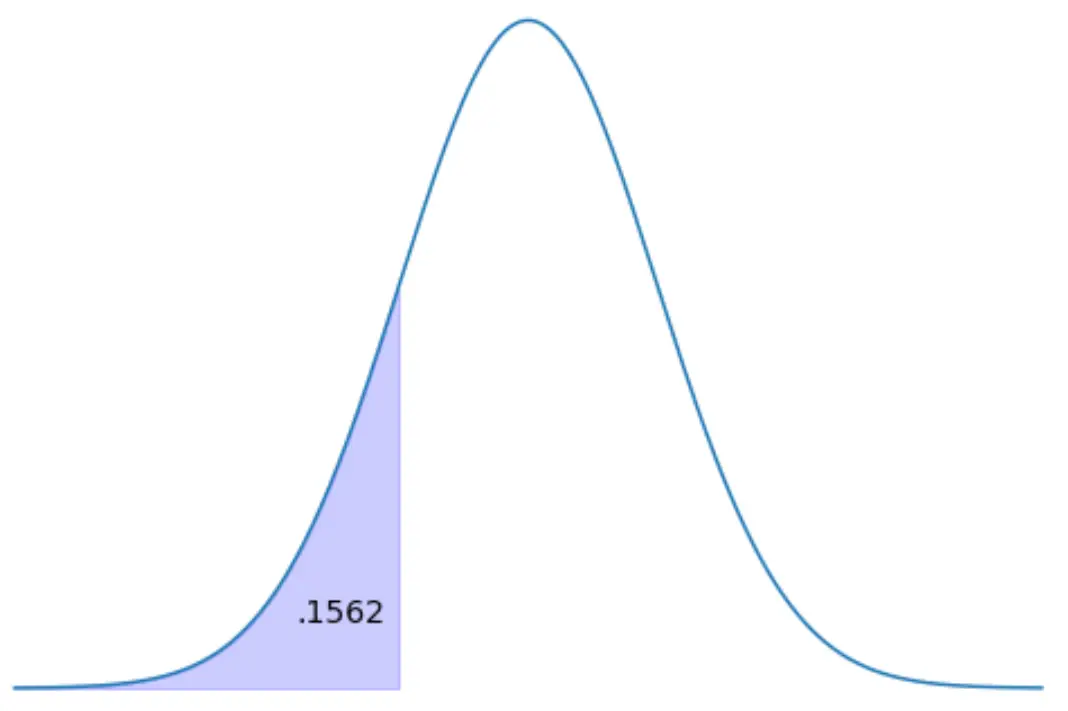
Contoh 1: Temukan luas skor Z di sebelah kiri
Temukan skor-z yang mewakili 15,62% dari wilayah distribusi di sebelah kiri.
Metode 1: Gunakan tabel z.
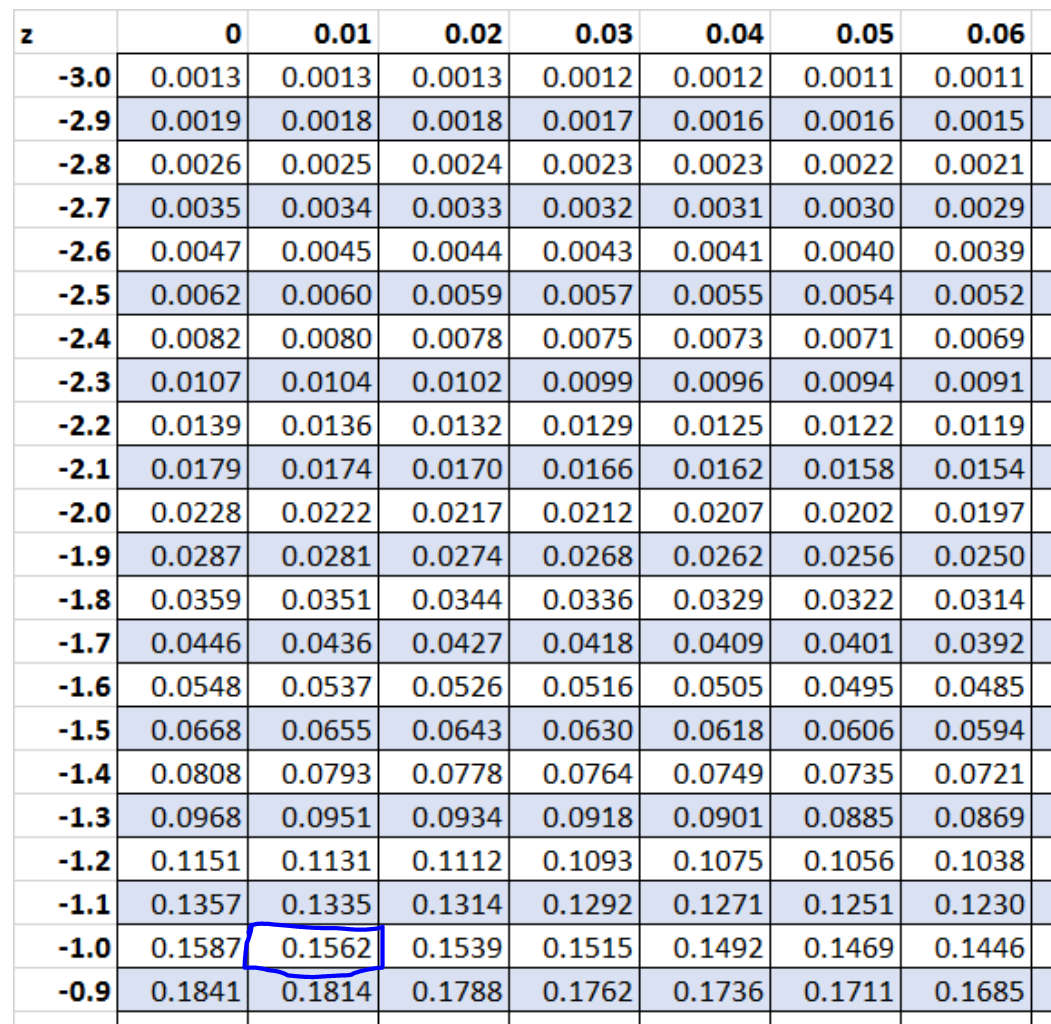
Skor-z yang sesuai dengan nilai 0,1562 pada tabel-z adalah -1,01 .
2. Gunakan kalkulator persentil skor Z.
Menurut kalkulator persentil skor-Z, skor-z yang sesuai dengan persentil 0,1562 adalah -1,01 .

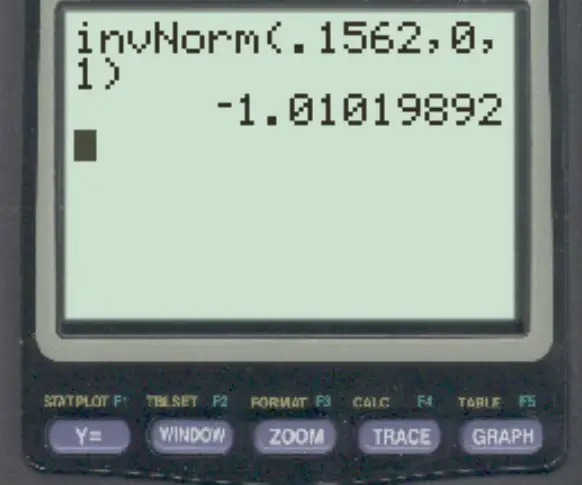
3. Gunakan fungsi invNorm() pada kalkulator TI-84.
Menggunakan fungsi invNorm() pada kalkulator TI-84, skor-z yang sesuai dengan luas 0,1562 di sebelah kiri adalah -1,01 .
Perhatikan bahwa ketiga metode tersebut menghasilkan hasil yang sama.
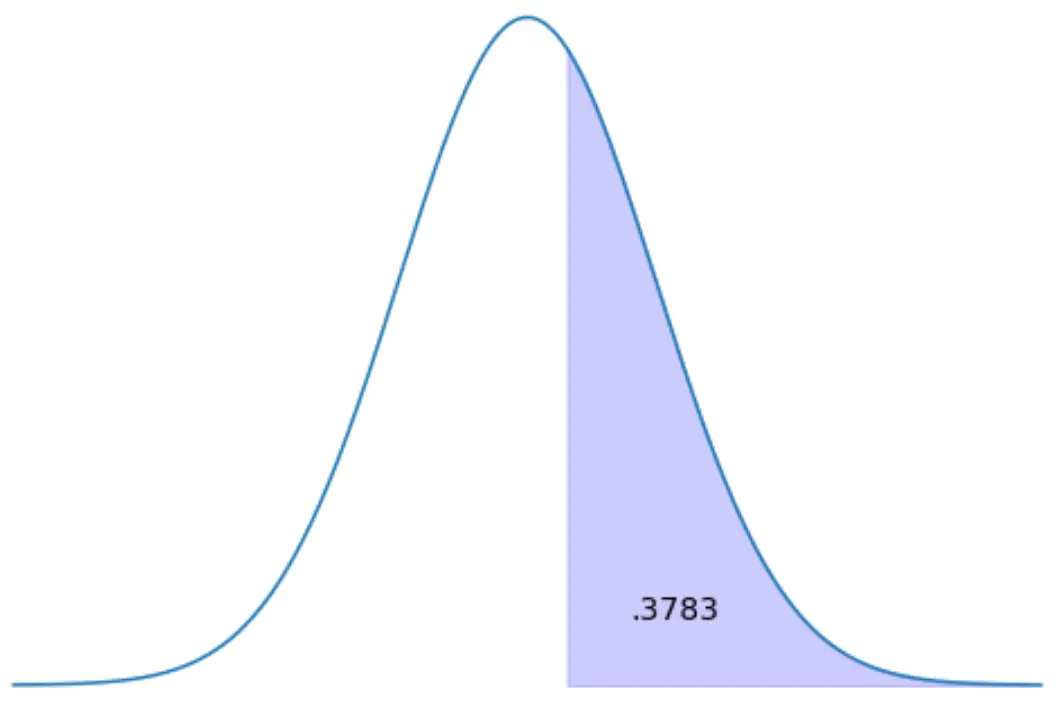
Contoh 2: Temukan area skor Z di sebelah kanan
Temukan skor-z yang mewakili 37,83% dari wilayah distribusi di sebelah kanan.
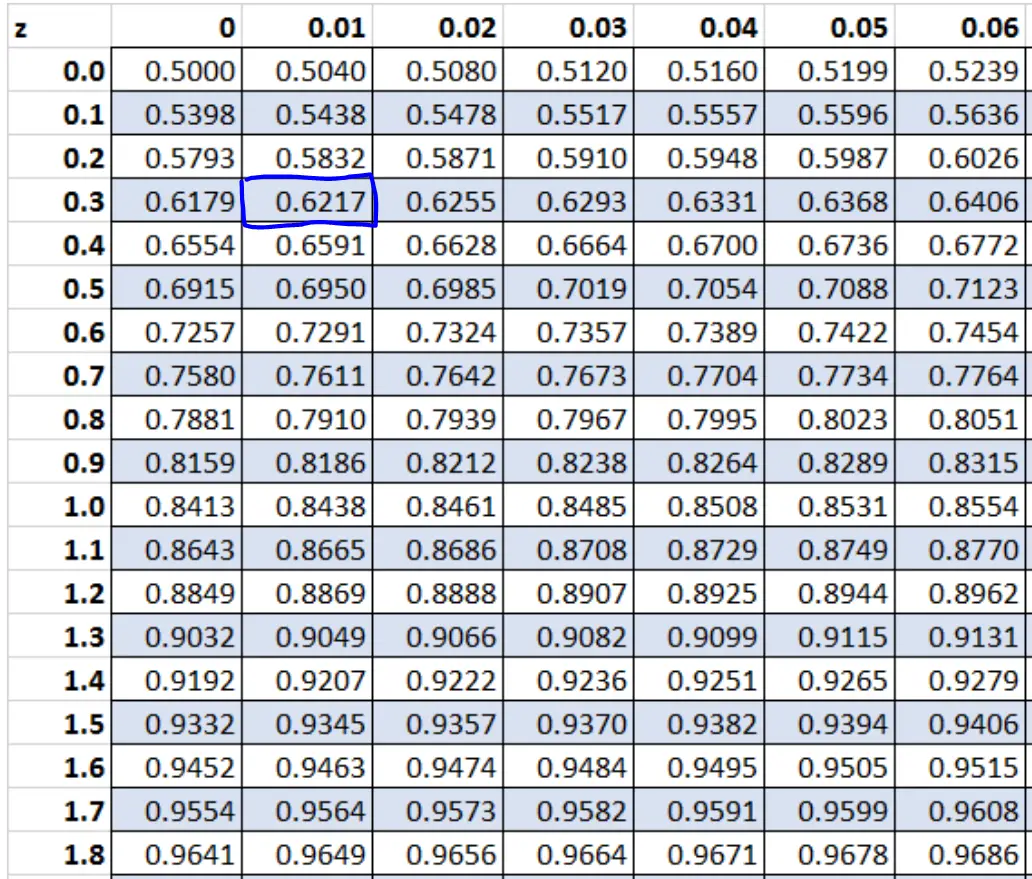
Metode 1: Gunakan tabel z.
Bagan z menunjukkan area di sebelah kiri skor z yang berbeda. Jadi, jika kita mengetahui luas di sebelah kanan adalah 0,3783, maka luas di sebelah kiri adalah 1 – 0,3783 = 0,6217.
Skor-z yang sesuai dengan nilai 0,6217 pada tabel-z adalah 0,31.
2. Gunakan kalkulator persentil skor Z.
Menurut kalkulator persentil skor-Z, skor-z yang sesuai dengan persentil 0,6217 adalah. 3099 .

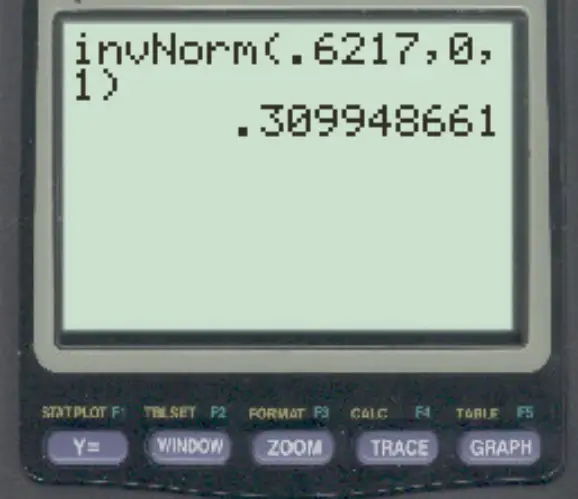
3. Gunakan fungsi invNorm() pada kalkulator TI-84.
Menggunakan fungsi invNorm() pada kalkulator TI-84, skor-z yang sesuai dengan luas 0,6217 di sebelah kiri adalah 0,3099 .
Contoh 3: Menemukan skor Z di area antara dua nilai
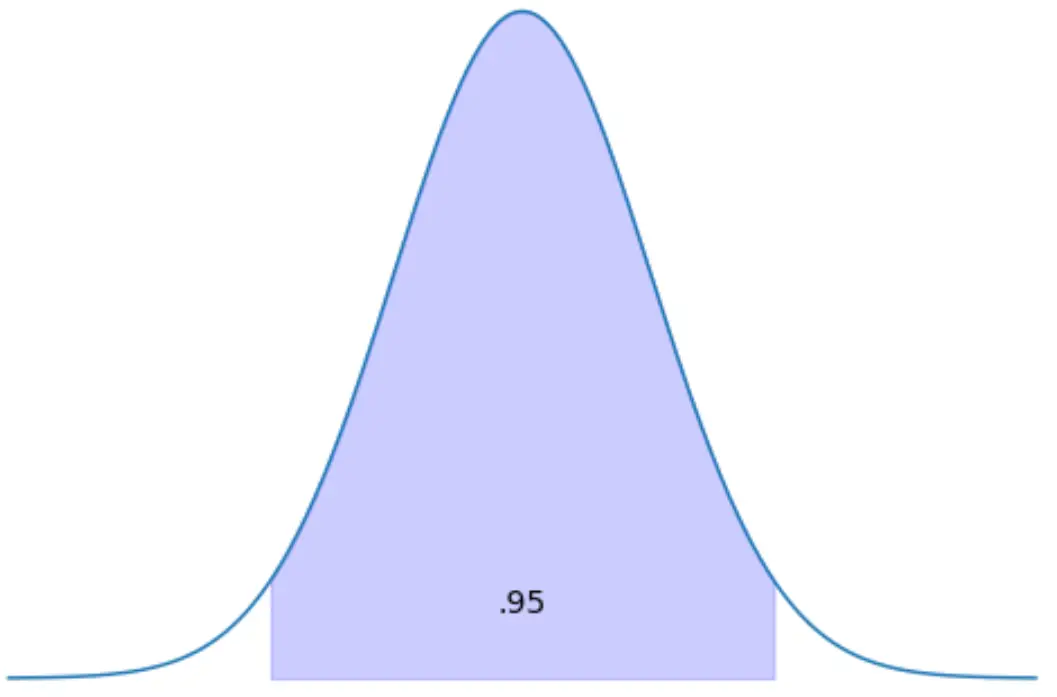
Temukan skor-z yang memiliki 95% area distribusi di antara keduanya.
Metode 1: Gunakan tabel z.
Jika 95% distribusinya terletak di antara dua skor-z, berarti 5% distribusinya terletak di luar skor-z.
Jadi 2,5% distribusinya lebih rendah dari salah satu z-score dan 2,5% distribusinya lebih tinggi dari z-score lainnya.
Jadi kita bisa mencari 0,025 di tabel z. Skor-z yang sesuai dengan 0,025 pada tabel-z adalah -1,96 .
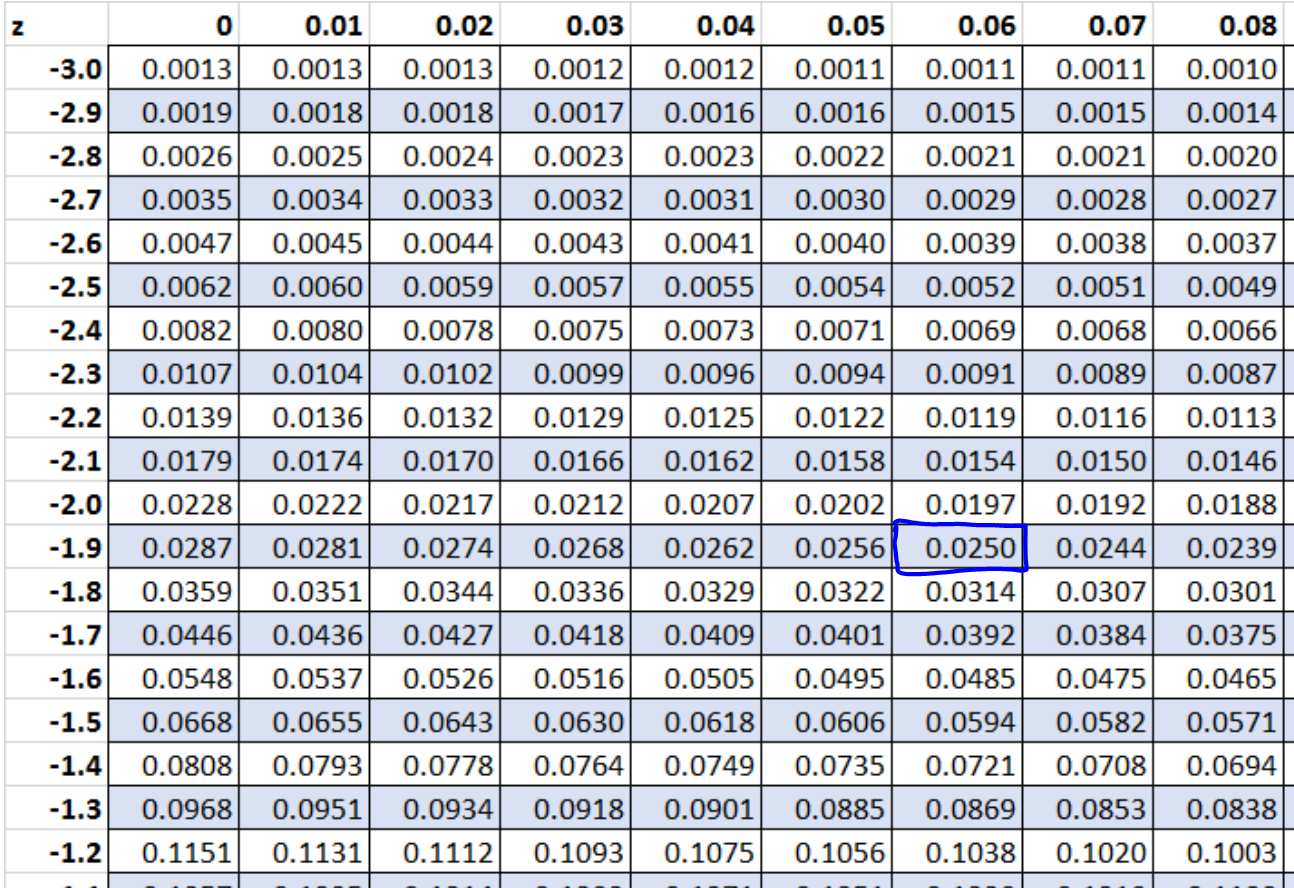
Jadi skor-z yang mengandung 95% distribusi di antara keduanya adalah -1.96 dan 1.96 .
2. Gunakan kalkulator persentil skor Z.
Menurut kalkulator persentil skor-Z, skor-z yang sesuai dengan persentil 0,025 adalah -1,96 .

Jadi skor-z yang mengandung 95% distribusi di antara keduanya adalah -1.96 dan 1.96 .
3. Gunakan fungsi invNorm() pada kalkulator TI-84.
Menggunakan fungsi invNorm() pada kalkulator TI-84, skor-z yang sesuai dengan luas 0,025 di sebelah kiri adalah -1,96 .
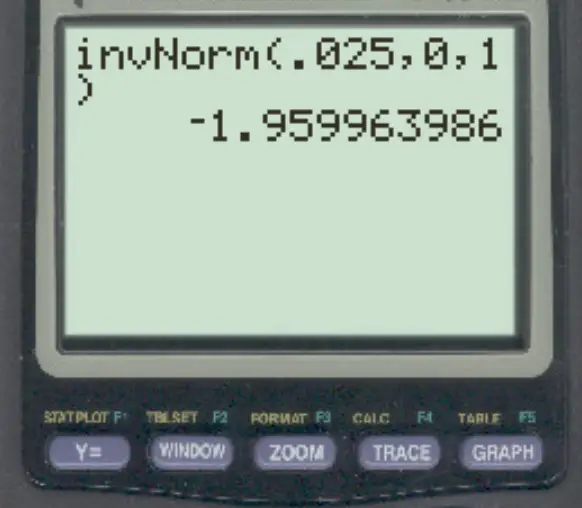
Jadi skor-z yang mengandung 95% distribusi di antara keduanya adalah -1.96 dan 1.96 .