Cara menerapkan teorema limit pusat pada kalkulator ti-84

Teorema limit pusat menyatakan bahwa distribusi sampling dari mean sampel mendekati normal jika ukuran sampel cukup besar, meskipun distribusi populasi tidak normal.

Teorema limit pusat juga menyatakan bahwa distribusi sampling akan mempunyai sifat-sifat sebagai berikut:

1. Rata-rata distribusi sampling akan sama dengan rata-rata distribusi populasi:

x = μ

2. Simpangan baku distribusi sampling akan sama dengan simpangan baku populasi dibagi dengan jumlah sampel:

s = σ / √n

Untuk mencari probabilitas terkait mean sampel pada kalkulator TI-84, kita dapat menggunakan fungsi normalcdf() dengan sintaks berikut:

 normalcdf (lower value, upper value, x , s/√ n )

Emas:

• x : mean sampel
• s : deviasi standar sampel
• n : ukuran sampel

Untuk mengakses fungsi ini pada kalkulator TI-84, cukup tekan 2 lalu tekan VARS lalu gulir ke normalcdf ( dan tekan ENTER .

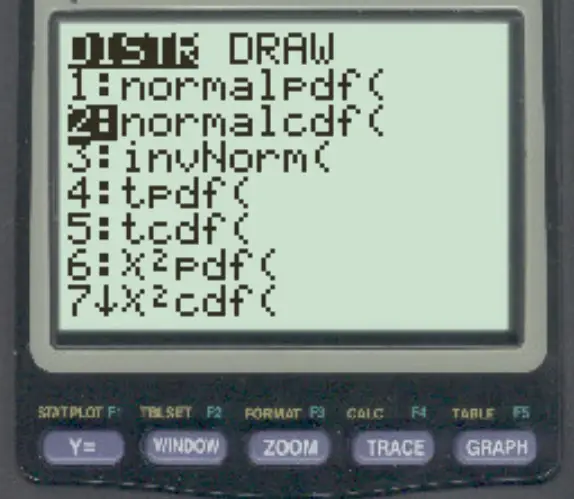
Contoh berikut menunjukkan cara menggunakan fungsi ini dalam praktiknya.

Contoh 1: Temukan probabilitas antara dua nilai

Suatu distribusi mempunyai rata-rata 70 dan simpangan baku 7. Jika kita memilih sampel acak berukuran n = 35, carilah probabilitas bahwa rata-rata sampel adalah antara 68 dan 72.

Kita dapat menggunakan sintaks berikut pada TI-84:

 normalcdf (68, 72, 70, 7/√ 35 ) 

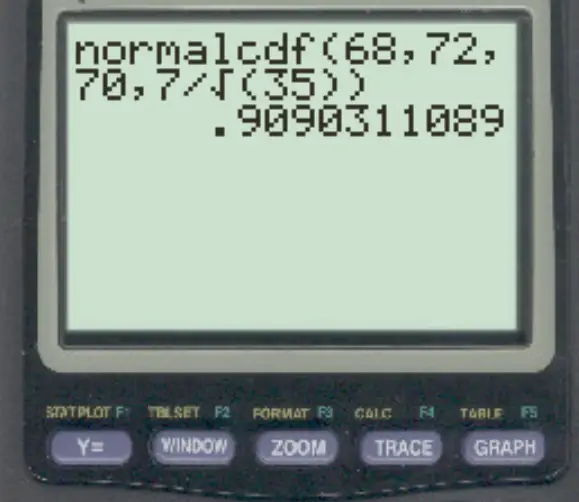
Probabilitas mean sampel antara 68 dan 72 adalah 0,909 .

Contoh 2: Menemukan probabilitas yang lebih besar dari suatu nilai

Suatu distribusi mempunyai rata-rata 50 dan simpangan baku 4. Jika kita memilih sampel acak berukuran n = 30, carilah probabilitas bahwa rata-rata sampel lebih besar dari 48.

Kita dapat menggunakan sintaks berikut pada TI-84:

 normalcdf (48, E99, 50, 4/√ 30 )

Catatan: Anda dapat mengakses simbol “E” dengan menekan 2 , lalu menekan tombol , .

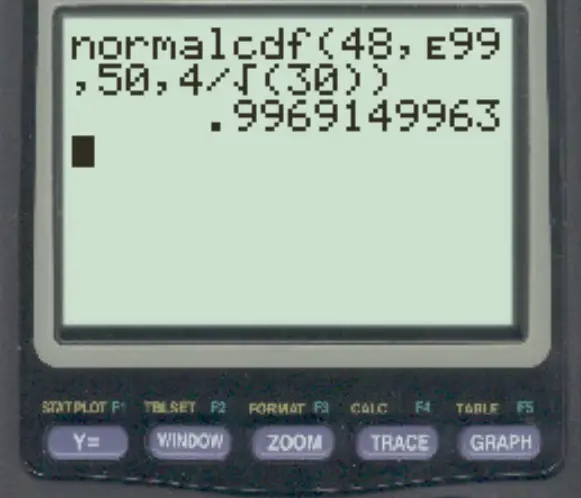
Probabilitas mean sampel lebih besar dari 48 adalah 0,9969 .

Contoh 3: Menemukan probabilitas yang kurang dari suatu nilai

Suatu distribusi mempunyai rata-rata 20 dan simpangan baku 3. Jika kita memilih sampel acak berukuran n = 40, carilah probabilitas bahwa rata-rata sampel kurang dari 19.

Kita dapat menggunakan sintaks berikut pada TI-84:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

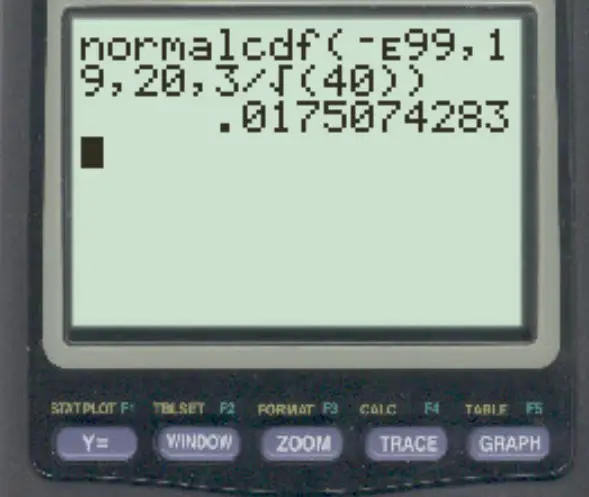
Probabilitas mean sampel kurang dari 19 adalah 0,0175 .

Sumber daya tambahan

Pengantar Teorema Limit Pusat
Kalkulator Teorema Batas Pusat
Cara Menerapkan Teorema Limit Pusat di Excel
Teorema limit pusat: empat syarat yang harus dipenuhi