R vs r-square: apa bedanya?
Dua istilah yang sering membingungkan siswa dalam statistika adalah R dan R-squared , sering ditulis R2 .
Dalam konteks regresi linier sederhana :
- A: Korelasi antara variabel prediktor x dengan variabel respon y.
- R 2 : Proporsi varians variabel respon yang dapat dijelaskan oleh variabel prediktor dalam model regresi.
Dan dalam konteks regresi linier berganda :
- A: Korelasi antara nilai observasi variabel respon dan nilai prediksi variabel respon yang dibuat oleh model.
- R 2 : Proporsi varians variabel respon yang dapat dijelaskan oleh variabel prediktor model regresi.
Perhatikan bahwa nilai R 2 adalah antara 0 dan 1. Semakin mendekati nilai 1, semakin kuat hubungan antara variabel prediktor dan variabel respon.
Contoh berikut menunjukkan cara menginterpretasikan nilai R dan R-kuadrat dalam model regresi linier sederhana dan regresi linier berganda.
Contoh 1: Regresi linier sederhana
Misalkan kita memiliki kumpulan data berikut yang menunjukkan jam belajar dan nilai ujian yang diperoleh 12 siswa dalam mata pelajaran matematika tertentu:
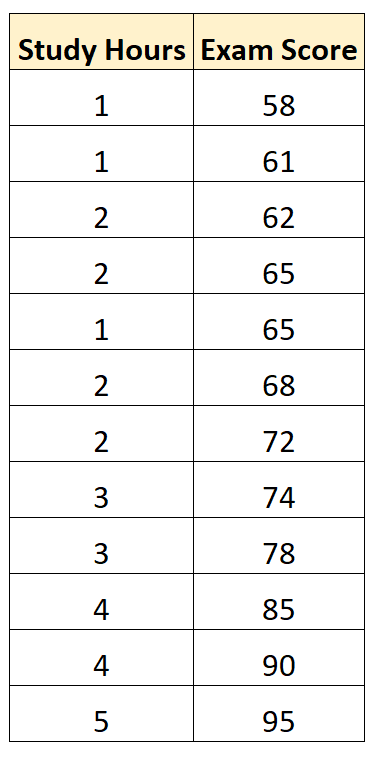
Dengan menggunakan perangkat lunak statistik (seperti Excel, R, Python, SPSS, dll.), kita dapat menyesuaikan model regresi linier sederhana dengan menggunakan “jam belajar” sebagai variabel prediktor dan “nilai ujian” sebagai variabel respons .
Kita dapat menemukan keluaran berikut untuk model ini:
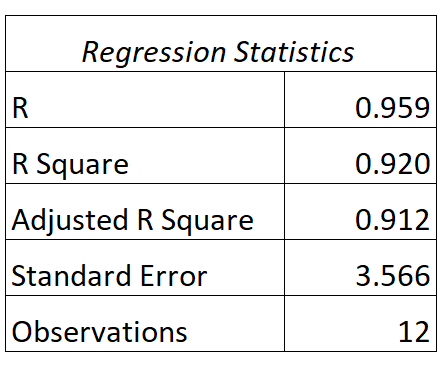
Berikut cara menginterpretasikan nilai R dan R kuadrat model ini:
- A: Korelasi antara jam belajar dan nilai ujian adalah 0,959 .
- R 2 : R kuadrat untuk model regresi ini adalah 0,920 . Hal ini menunjukkan bahwa 92,0% variasi nilai ujian dapat dijelaskan oleh jumlah jam belajar.
Perhatikan juga bahwa nilai R 2 sama dengan nilai R, dikuadratkan:
R2 = R * R = 0,959 * 0,959 = 0,920
Contoh 2: Regresi linier berganda
Misalkan kita memiliki kumpulan data berikut yang menunjukkan jam belajar, nilai siswa saat ini, dan nilai ujian yang diperoleh 12 siswa dalam mata pelajaran matematika tertentu:
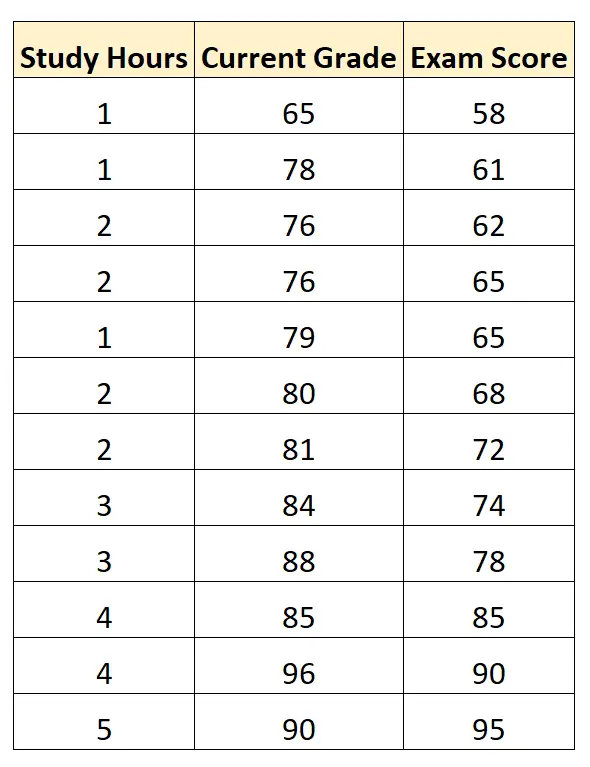
Dengan menggunakan perangkat lunak statistik, kita dapat menyesuaikan model regresi linier berganda dengan menggunakan “jam belajar” dan “nilai saat ini” sebagai variabel prediktor dan “nilai ujian” sebagai variabel respon.
Kita dapat menemukan keluaran berikut untuk model ini:
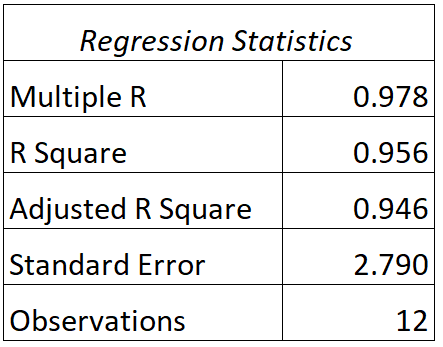
Berikut cara menginterpretasikan nilai R dan R kuadrat model ini:
- J: Korelasi antara nilai tes aktual dan prediksi nilai tes model adalah 0,978 .
- R 2 : R kuadrat untuk model regresi ini adalah 0,956 . Hal ini menunjukkan bahwa 95,6% variasi nilai ujian dapat dijelaskan oleh jumlah jam belajar dan nilai siswa saat ini di kelas.
Perhatikan juga bahwa nilai R 2 sama dengan nilai R, dikuadratkan:
R2 = R * R = 0,978 * 0,978 = 0,956
Sumber daya tambahan
Berapa nilai R-kuadrat yang bagus?
Panduan Lembut tentang Jumlah Kuadrat: SST, SSR, SSE