Bagaimana mencari probabilitas berdasarkan mean dan deviasi standar

Kita dapat menggunakan proses berikut untuk mencari probabilitas suatu variabel acak berdistribusi normal

Langkah 1: Temukan skor-z.

Skor-z memberi tahu Anda berapa banyak standar deviasi suatu nilai data individual yang turun dari rata-ratanya. Ini dihitung sebagai berikut:

skor-z = (x – μ) / σ

Emas:

• x: nilai data individu
• μ: rata-rata populasi
• σ: deviasi standar populasi

Langkah 2: Temukan probabilitas yang sesuai dengan skor-z.

Setelah kita menghitung skor z, kita dapat menemukan probabilitasnya di tabel z.

Contoh berikut menunjukkan cara menggunakan proses ini dalam skenario yang berbeda.

Contoh 1: Probabilitas kurang dari nilai tertentu

Nilai suatu tes tertentu berdistribusi normal dengan mean μ = 82 dan standar deviasi σ = 8. Berapakah probabilitas bahwa seorang siswa mendapat nilai kurang dari 84 pada tes tersebut?

Langkah 1: Temukan skor-z.

Pertama, kita akan mencari skor-z yang terkait dengan skor 84:

skor-z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Langkah 2: Gunakan tabel z untuk mencari probabilitas yang sesuai.

Selanjutnya kita akan mencari nilai 0,25 pada tabel z:

Kemungkinan seorang siswa tertentu akan mendapat nilai kurang dari 84 adalah sekitar 59,87% .

Contoh 2: Probabilitas lebih besar dari nilai tertentu

Tinggi badan suatu spesies penguin tertentu berdistribusi normal dengan rata-rata μ = 30 inci dan simpangan baku σ = 4 inci. Jika kita memilih seekor penguin secara acak, berapa peluang terambilnya seekor penguin dengan tinggi lebih dari 28 inci?

Langkah 1: Temukan skor-z.

Pertama, kita akan menemukan skor-z yang terkait dengan tinggi 28 inci.

Skor z = (x – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0,5

Langkah 2: Gunakan tabel z untuk mencari probabilitas yang sesuai.

Selanjutnya kita akan mencari nilai -0.5   di tabel z:

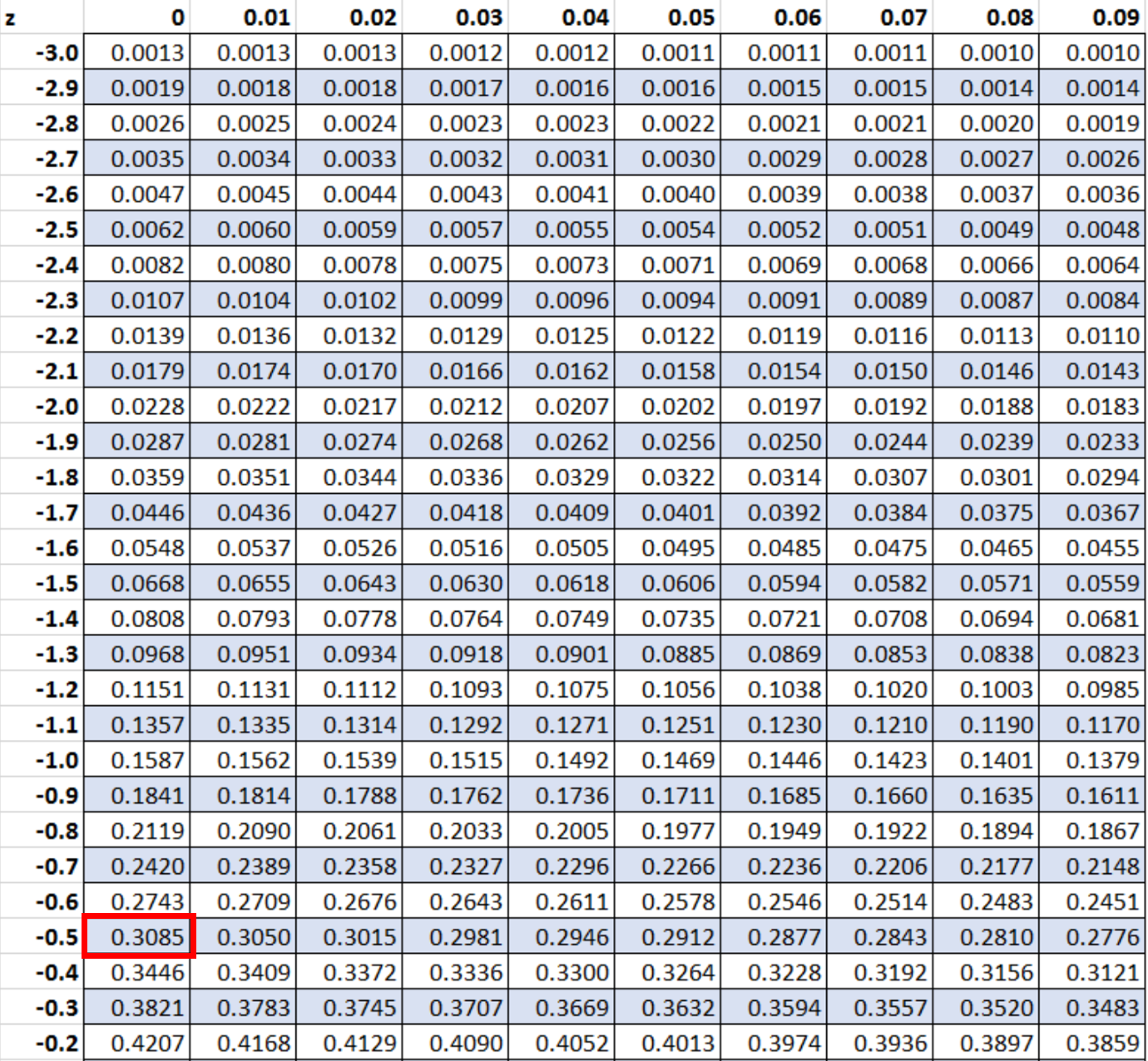
Nilai yang sesuai dengan skor-z -0,5 adalah 0,3085. Ini menunjukkan kemungkinan seekor penguin akan lebih pendek dari 28 inci.

Namun, karena kita ingin mengetahui probabilitas seekor penguin lebih tinggi dari 28 inci, kita perlu mengurangkan probabilitas tersebut dari 1.

Jadi, peluang seekor penguin yang tingginya lebih dari 28 inci adalah: 1 – 0,3085 = 0,6915 .

Contoh 3: Probabilitas antara dua nilai

Berat suatu spesies penyu tertentu berdistribusi normal dengan rata-rata μ = 400 pon dan simpangan baku σ = 25 pon. Jika kita memilih seekor kura-kura secara acak, berapakah probabilitas bahwa kura-kura tersebut memiliki berat antara 410 dan 425 pon?

Langkah 1: Temukan skor-z.

Pertama, kita akan menemukan skor-z yang terkait dengan 410 buku dan 425 buku

z-skor 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

z skor 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Langkah 2: Gunakan tabel z untuk mencari probabilitas yang sesuai.

Pertama, kita akan mencari nilai 0,4   di tabel z:

Selanjutnya kita akan mencari nilai 1   di tabel z:

Selanjutnya, kita akan mengurangkan nilai yang lebih kecil dari nilai yang lebih besar: 0.8413 – 0.6554 = 0.1859 .

Jadi peluang terambilnya kura-kura yang dipilih secara acak memiliki berat antara 410 pon dan 425 pon adalah 18,59% .

Sumber daya tambahan

Cara menghitung nilai P secara manual dari skor Z
Bagaimana mengkonversi skor Z menjadi skor mentah
Bagaimana menemukan skor Z di area tertentu