Bagaimana menafsirkan kesalahan akar rata-rata kuadrat (rmse)

Analisis regresi adalah teknik yang dapat kita gunakan untuk memahami hubungan antara satu atau lebih variabel prediktor dan variabel respon .

Salah satu cara untuk mengevaluasi seberapa cocok model regresi dengan kumpulan data adalah dengan menghitung mean squared error , yaitu metrik yang memberi tahu kita jarak rata-rata antara nilai prediksi model dan nilai sebenarnya dari kumpulan data.

Semakin rendah RMSE, semakin baik model tertentu mampu “menyesuaikan” kumpulan data.

Rumus untuk mencari mean square error yang sering disingkat RMSE adalah:

RMSE = √ Σ(P _saya – O _saya ) ² / n

Emas:

• Σ adalah simbol mewah yang berarti “jumlah”
• P _i adalah nilai prediksi observasi ^ke-i dalam dataset
• O _i adalah nilai observasi untuk observasi ^ke-i dalam kumpulan data
• n adalah ukuran sampel

Contoh berikut menunjukkan cara menafsirkan RMSE untuk model regresi tertentu.

Contoh: Cara menginterpretasikan RMSE untuk model regresi

Misalkan kita ingin membangun model regresi yang menggunakan “jam belajar” untuk memprediksi “nilai ujian” siswa pada ujian masuk perguruan tinggi tertentu.

Kami mengumpulkan data berikut untuk 15 siswa:

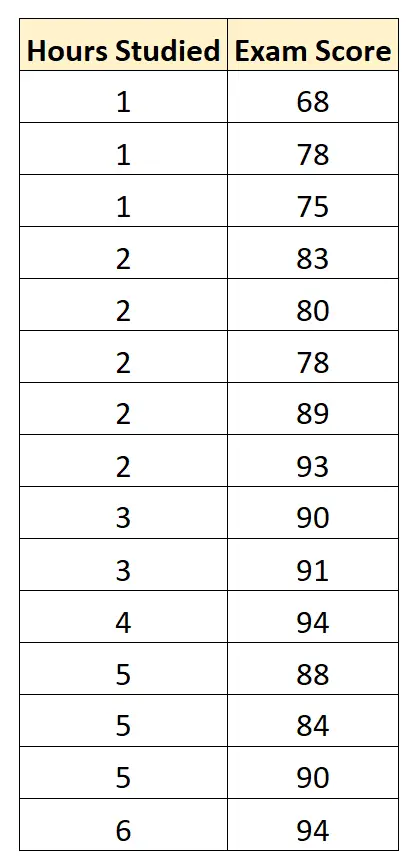
Kami kemudian menggunakan perangkat lunak statistik (seperti Excel, SPSS, R, Python), dll. untuk menemukan model regresi yang sesuai berikut:

Nilai ujian = 75,95 + 3,08* (jam belajar)

Kita kemudian dapat menggunakan persamaan ini untuk memprediksi nilai ujian setiap siswa, berdasarkan jumlah jam belajar mereka:

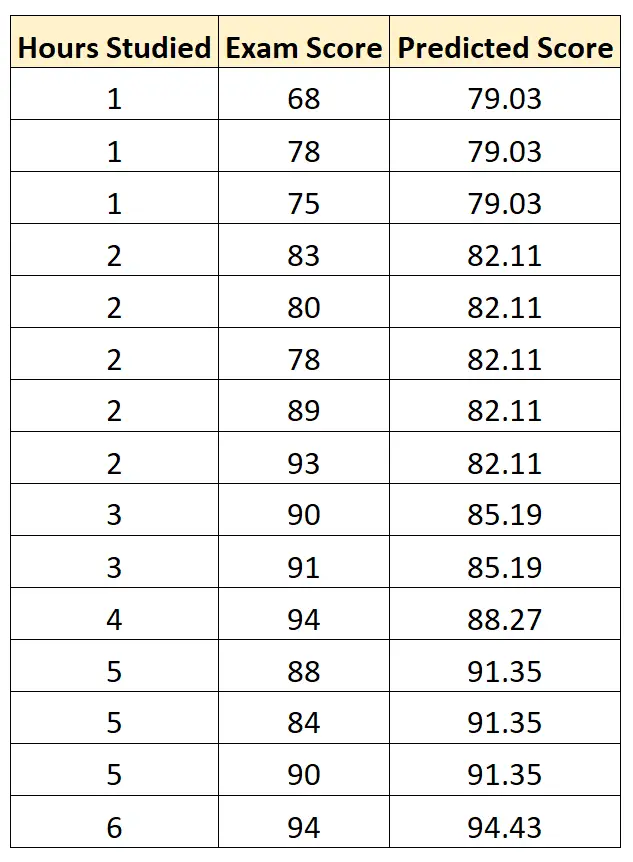
Kami kemudian dapat menghitung selisih kuadrat antara setiap nilai ujian yang diprediksi dan nilai ujian sebenarnya. Kita kemudian dapat mengambil akar kuadrat dari rata-rata perbedaan berikut:

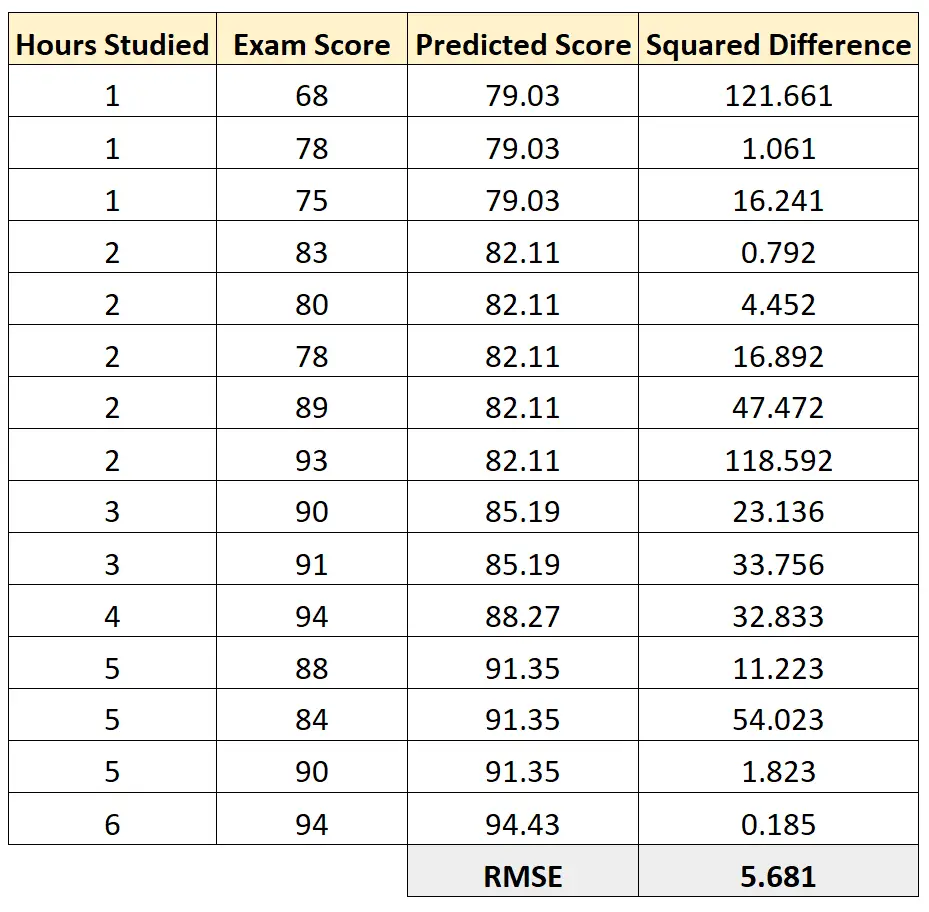
RMSE model regresi ini ternyata 5,681 .

Ingatlah bahwa residu model regresi adalah perbedaan antara nilai data yang diamati dan nilai prediksi model.

Sisa = (P _saya – O _saya )

Emas

• P _i adalah nilai prediksi observasi ^ke-i dalam dataset
• O _i adalah nilai observasi untuk observasi ^ke-i dalam kumpulan data

Dan ingat bahwa RMSE model regresi dihitung sebagai berikut:

RMSE = √ Σ(P _saya – O _saya ) ² / n

Artinya RMSE mewakili akar kuadrat dari varians residu.

Ini adalah nilai yang berguna untuk diketahui karena memberi kita gambaran tentang jarak rata-rata antara nilai data observasi dan nilai data prediksi.

Hal ini kontras dengan R-squared model, yang menunjukkan seberapa besar varians dalam variabel respons dapat dijelaskan oleh variabel prediktor model.

Perbandingan nilai RMSE model yang berbeda

RMSE sangat berguna untuk membandingkan kesesuaian model regresi yang berbeda.

Misalnya, kita ingin membangun model regresi untuk memprediksi nilai ujian siswa dan kita ingin mencari model terbaik di antara beberapa model potensial.

Misalkan kita memasangkan tiga model regresi yang berbeda dan menemukan nilai RMSE yang sesuai:

• RMSE model 1: 14.5
• RMSE model 2: 16.7
• RMSE model 3: 9.8

Model 3 memiliki RMSE terendah, yang menunjukkan bahwa model tersebut paling cocok dengan kumpulan data di antara tiga model potensial.

Sumber daya tambahan

Kalkulator RMSE
Cara Menghitung RMSE di Excel
Cara menghitung RMSE di R
Cara Menghitung RMSE dengan Python