Frekuensi (statistik)

Artikel ini menjelaskan apa pengertian frekuensi dalam statistik. Oleh karena itu, Anda akan menemukan definisi frekuensi dalam statistik, berbagai jenis frekuensi yang ada, dan terakhir, cara membuat tabel frekuensi.

Apa yang dimaksud dengan frekuensi dalam statistik?

Dalam statistik, frekuensi adalah berapa kali suatu nilai muncul dalam kumpulan data. Sederhananya, frekuensi adalah berapa kali suatu nilai diulang dalam sampel statistik.

Misalnya, jika dalam suatu survei lima orang menjawab warna kesukaannya adalah biru, maka frekuensi warna biru tersebut sama dengan 5.

Umumnya dalam ilmu statistika, huruf f dengan indeks i digunakan untuk menyatakan frekuensi dari nilai i , sehingga lambang frekuensinya adalah _fi .

Jumlah semua frekuensi memberikan jumlah total data dalam sampel. Oleh karena itu, rumus berikut selalu berlaku untuk setiap studi statistik:

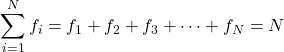
Emas

adalah frekuensi nilainya

Dan

adalah jumlah total pengamatan.

Jenis frekuensi dalam statistik

Dalam statistik, berbagai jenis frekuensi adalah sebagai berikut:

• Frekuensi absolut : sesuai dengan berapa kali suatu nilai muncul dalam sampel statistik.
• Frekuensi Absolut Kumulatif : Dihitung dengan menjumlahkan frekuensi absolut dari suatu nilai ditambah frekuensi absolut dari semua nilai yang lebih kecil.
• Frekuensi relatif : ini adalah frekuensi absolut dibagi dengan jumlah total data.
• Frekuensi Relatif Kumulatif : Sama dengan jumlah frekuensi relatif suatu nilai ditambah frekuensi relatif semua nilai yang lebih rendah.

Pada bagian di bawah ini Anda dapat melihat cara setiap jenis frekuensi dihitung.

Tabel frekuensi

Biasanya dalam statistik, penghitungan frekuensi sampel data dirangkum dalam tabel frekuensi. Di bawah ini adalah contoh langkah demi langkah sehingga Anda dapat melihat cara melakukannya.

• Nilai yang diperoleh pada mata pelajaran statistika pada kelas yang berjumlah 30 siswa adalah sebagai berikut. Buatlah tabel frekuensi kumpulan data.

Karena semua bilangan hanya dapat berupa bilangan bulat, maka bilangan tersebut merupakan variabel diskrit. Oleh karena itu, tidak perlu mengelompokkan data ke dalam interval.

Jadi kita perlu membuat tabel di mana setiap nilai yang berbeda akan menjadi satu baris. Selain itu, kita perlu mencari frekuensi absolut setiap nilai, untuk melakukannya, cukup hitung berapa kali nilai tersebut muncul dalam sampel data.

Perhatikan bahwa jumlah semua frekuensi absolut sama dengan jumlah total data. Jika aturan ini tidak dipatuhi, berarti Anda lupa memberikan informasi tertentu.

Sekarang setelah kita mengetahui frekuensi absolutnya, kita perlu mencari frekuensi absolut kumulatifnya. Untuk perhitungan ini kita mempunyai dua pilihan: kita menambahkan frekuensi absolut dari nilai ditambah semua frekuensi absolut dari nilai terkecil, atau sebaliknya, kita menambahkan frekuensi absolut dari nilai ditambah frekuensi absolut kumulatif dari nilai sebelumnya.

Frekuensi absolut kumulatif dari nilai terakhir selalu sesuai dengan jumlah total data, Anda dapat menggunakan trik ini untuk memverifikasi bahwa perhitungannya benar.

Selanjutnya, kita perlu menentukan frekuensi relatif, yang dihitung dengan membagi frekuensi absolut dengan jumlah titik data (30):

Perlu diingat bahwa jumlah semua frekuensi relatif selalu sama dengan 1, jika tidak maka beberapa perhitungan pada tabel frekuensi salah.

Terakhir, cukup mengekstrak akumulasi frekuensi relatif. Untuk melakukan ini, Anda harus menambahkan frekuensi relatif dari nilai yang dimaksud ditambah semua frekuensi relatif sebelumnya atau, yang jumlahnya sama, akumulasi frekuensi relatif sebelumnya:

Secara singkat tabel frekuensi dengan seluruh frekuensi data yang bermasalah adalah sebagai berikut: