Rmse vs. r-squared: metrik mana yang harus anda gunakan?

Model regresi digunakan untuk mengukur hubungan antara satu atau lebih variabel prediktor dan variabel respon.

Kapan pun kami menyesuaikan model regresi, kami ingin memahami seberapa cocok model tersebut dengan data. Dengan kata lain, seberapa baik model tersebut mampu menggunakan nilai variabel prediktor untuk memprediksi nilai variabel respon ?

Dua metrik yang sering digunakan ahli statistik untuk mengukur seberapa cocok suatu model dengan kumpulan data adalah root mean square error (RMSE) dan R squared ( ^R2 ), yang dihitung sebagai berikut:

RMSE : metrik yang memberi tahu kita seberapa jauh rata-rata nilai prediksi dari nilai observasi dalam kumpulan data. Semakin rendah RMSE, semakin baik model tersebut cocok dengan kumpulan data.

Ini dihitung sebagai berikut:

RMSE = √ Σ(P _saya – O _saya ) ² / n

Emas:

• Σ adalah simbol yang berarti “jumlah”
• P _i adalah nilai prediksi pengamatan ^ke-i
• O _i adalah nilai observasi untuk observasi ^ke-i
• n adalah ukuran sampel

R ² : Metrik yang memberi tahu kita seberapa besar varians variabel respons suatu model regresi dapat dijelaskan oleh variabel prediktor. Nilai ini antara 0 dan 1. Semakin tinggi nilai R ² , semakin baik model tersebut cocok dengan sekumpulan data.

Ini dihitung sebagai berikut:

^R2 = 1 – (RSS/TSS)

Emas:

• RSS mewakili jumlah kuadrat dari residu
• TSS mewakili jumlah total kuadrat

RMSE vs R ² : Metrik Mana yang Harus Anda Gunakan?

Saat mengevaluasi kesesuaian model dengan kumpulan data, akan berguna untuk menghitung nilai RMSE dan nilai R ² , karena setiap metrik memberi tahu kita sesuatu yang berbeda.

Di satu sisi, RMSE memberi tahu kita jarak tipikal antara nilai prediksi yang dibuat oleh model regresi dan nilai sebenarnya.

Di sisi lain, R ² memberitahu kita sejauh mana variabel prediktor dapat menjelaskan variasi variabel respon.

Misalnya, kita memiliki kumpulan data berikut yang menampilkan informasi tentang rumah di kota tertentu:

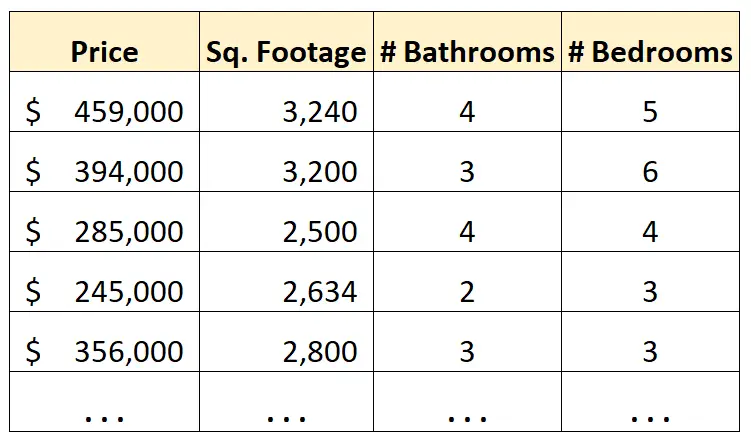
Sekarang katakanlah kita ingin menggunakan luas persegi, jumlah kamar mandi, dan jumlah kamar tidur untuk memprediksi harga sebuah rumah.

Kita dapat mengadaptasi model regresi berikut:

Harga = β ₀ + β ₁ (luas persegi) + β ₂ (# kamar mandi) + β ₃ (# kamar tidur)

Sekarang anggaplah kita cocok dengan model ini, lalu hitung metrik berikut untuk mengevaluasi kesesuaian model:

• RMSE : 14.342
• ^R2 : 0,856

Nilai RMSE menunjukkan bahwa perbedaan rata-rata antara prediksi harga rumah model dan harga rumah sebenarnya adalah $14.342.

Nilai R ² menunjukkan bahwa variabel prediktor model (ukuran luas, jumlah kamar mandi, dan jumlah kamar tidur) mampu menjelaskan 85,6% variasi harga rumah.

Untuk menentukan apakah nilai-nilai tersebut “baik” atau tidak, kita dapat membandingkan pengukuran tersebut dengan model alternatif.

Misalnya, kita menyesuaikan model regresi lain yang menggunakan kumpulan variabel prediktor berbeda dan menghitung metrik berikut untuk model tersebut:

• RMSE : 19.355
• ^R2 : 0,765

Terlihat nilai RMSE model ini lebih tinggi dibandingkan model sebelumnya. Terlihat juga nilai R ² model ini lebih rendah dibandingkan model sebelumnya. Hal ini menunjukkan bahwa model ini kurang cocok dengan data dibandingkan model sebelumnya.

Ringkasan

Berikut poin-poin utama yang diangkat dalam artikel ini:

• RMSE dan R ² mengukur seberapa cocok model regresi dengan kumpulan data.
• RMSE memberi tahu kita seberapa baik model regresi dapat memprediksi nilai variabel respons secara absolut, sedangkan R ² memberi tahu kita seberapa baik model dapat memprediksi nilai variabel respons dalam persentase.
• Menghitung RMSE dan ^R2 untuk model tertentu berguna karena setiap metrik memberi kita informasi yang berguna.

Sumber daya tambahan

Pengantar Regresi Linier Berganda
R vs R-Square: apa bedanya?
Berapa nilai R-kuadrat yang bagus?