Kapan menggunakan regresi ridge & lasso
Dalam regresi linier berganda biasa, kami menggunakan sekumpulan variabel prediktor p dan variabel respons agar sesuai dengan model dalam bentuk:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p
Nilai β 0 , β 1 , B 2 , …, β p dipilih menggunakan metode kuadrat terkecil, yang meminimalkan jumlah kuadrat residu (RSS):
RSS = Σ(y saya – ŷ saya ) 2
Emas:
- Σ : Simbol yang berarti “jumlah”
- y i : nilai respon sebenarnya untuk observasi ke-i
- ŷ i : Nilai respon yang diprediksi untuk observasi ke- i
Masalah multikolinearitas dalam regresi
Masalah yang sering muncul dalam praktik regresi linier berganda adalah multikolinearitas – ketika dua atau lebih variabel prediktor berkorelasi tinggi satu sama lain, sehingga tidak memberikan informasi unik atau independen dalam model regresi.
Hal ini dapat membuat estimasi koefisien model tidak dapat diandalkan dan menunjukkan varians yang tinggi. Artinya, ketika model diterapkan pada kumpulan data baru yang belum pernah ada sebelumnya, kemungkinan besar kinerjanya akan buruk.
Menghindari multikolinearitas: Regresi Ridge & Lasso
Dua metode yang dapat kita gunakan untuk mengatasi masalah multikolinearitas ini adalah regresi ridge dan regresi laso .
Regresi ridge berupaya meminimalkan hal-hal berikut:
- RSS + λΣβ j 2
Regresi Lasso berupaya meminimalkan hal-hal berikut:
- RSS + λΣ|β j |
Dalam kedua persamaan tersebut, suku kedua disebut penalti penarikan .
Ketika λ = 0, suku penalti ini tidak berpengaruh dan regresi ridge dan regresi laso menghasilkan estimasi koefisien yang sama dengan kuadrat terkecil.
Namun, ketika λ mendekati tak terhingga, penalti penyusutan menjadi lebih berpengaruh dan variabel prediktif yang tidak dapat diimpor ke dalam model berkurang menuju nol.
Dengan regresi Lasso, ada kemungkinan beberapa koefisien menjadi nol sepenuhnya ketika λ menjadi cukup besar.
Keuntungan dan Kerugian Regresi Ridge & Lasso
Keuntungan regresi Ridge dan Lasso dibandingkan regresi kuadrat terkecil adalah tradeoff bias-varians .
Ingatlah bahwa Mean Square Error (MSE) adalah metrik yang dapat kita gunakan untuk mengukur keakuratan model tertentu dan dihitung sebagai berikut:
MSE = Var( f̂( x 0 )) + [Bias( f̂( x 0 ))] 2 + Var(ε)
MSE = Varians + Bias 2 + Kesalahan yang tidak dapat direduksi
Ide dasar dari Regresi Ridge dan Regresi Lasso adalah untuk memperkenalkan bias kecil sehingga varians dapat dikurangi secara signifikan, sehingga menghasilkan UMK yang lebih rendah secara keseluruhan.
Untuk mengilustrasikannya, perhatikan grafik berikut:

Perhatikan bahwa ketika λ meningkat, variansnya berkurang secara signifikan dengan peningkatan bias yang sangat kecil. Namun, setelah melewati titik tertentu, varians berkurang dengan lebih cepat dan penurunan koefisien menyebabkan perkiraan yang terlalu rendah, sehingga menyebabkan peningkatan tajam dalam bias.
Kita dapat melihat dari grafik bahwa MSE pengujian paling rendah ketika kita memilih nilai λ yang menghasilkan trade-off optimal antara bias dan varians.
Ketika λ = 0, suku penalti dalam regresi laso tidak berpengaruh dan oleh karena itu menghasilkan estimasi koefisien yang sama dengan kuadrat terkecil. Namun, dengan meningkatkan λ hingga titik tertentu, kita dapat mengurangi MSE pengujian secara keseluruhan.
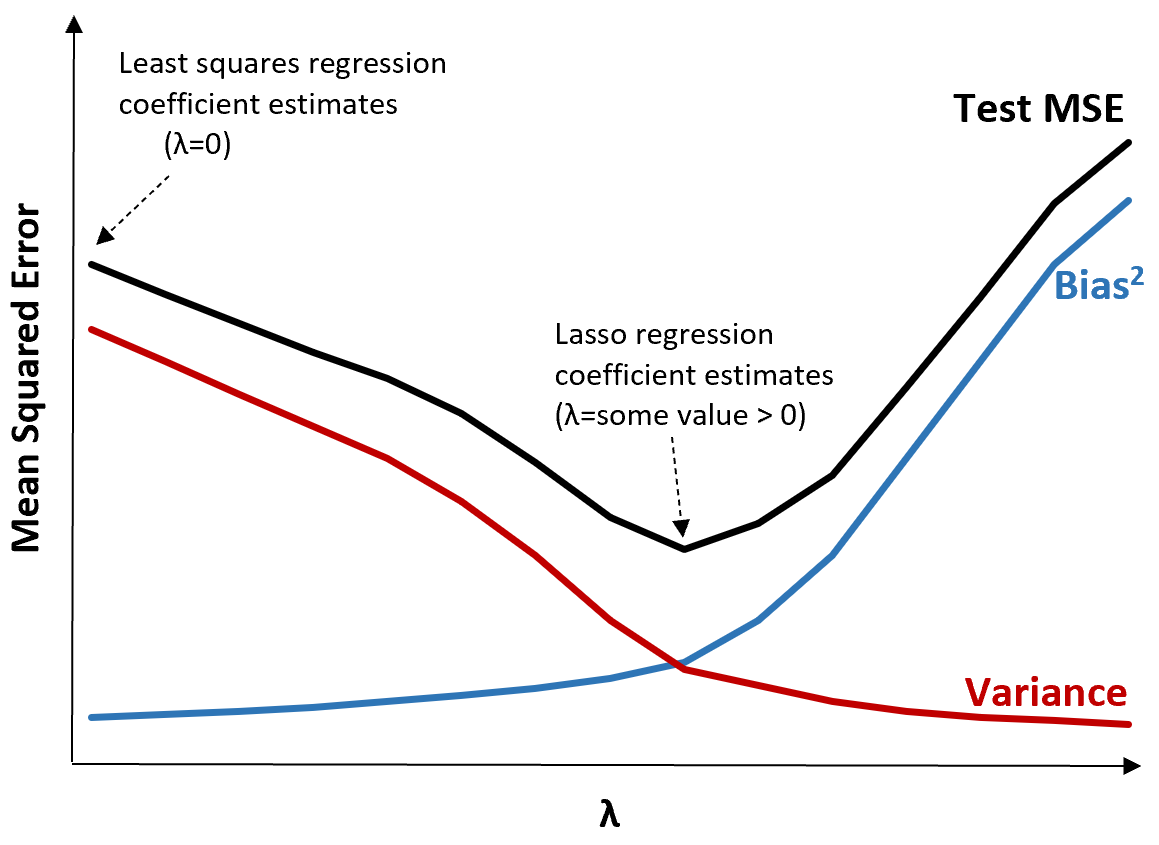
Artinya, pemasangan model dengan regresi ridge dan laso berpotensi menghasilkan kesalahan pengujian yang lebih kecil dibandingkan pemasangan model dengan regresi kuadrat terkecil.
Kerugian dari regresi Ridge dan Lasso adalah sulitnya menginterpretasikan koefisien dalam model akhir karena koefisiennya menyusut menuju nol.
Oleh karena itu, regresi Ridge dan Lasso harus digunakan ketika Anda ingin mengoptimalkan kemampuan prediktif daripada inferensi.
Punggungan vs. Regresi Lasso: Kapan Menggunakan Masing-masing
Regresi L asso dan regresi ridge dikenal sebagai metode regularisasi karena keduanya berupaya meminimalkan jumlah sisa kuadrat (RSS) serta jangka waktu penalti tertentu.
Dengan kata lain, mereka membatasi atau mengatur estimasi koefisien model.
Hal ini tentu saja menimbulkan pertanyaan: apakah regresi ridge atau laso lebih baik?
Dalam kasus di mana hanya sejumlah kecil variabel prediktor yang signifikan, regresi laso cenderung bekerja lebih baik karena mampu mereduksi sepenuhnya variabel-variabel yang tidak signifikan menjadi nol dan menghapusnya dari model.
Namun, ketika banyak variabel prediktor signifikan dalam model dan koefisiennya kira-kira sama, regresi ridge cenderung bekerja lebih baik karena semua prediktor tetap berada dalam model.
Untuk menentukan model mana yang terbaik untuk membuat prediksi, kami biasanya melakukan validasi silang k-fold dan memilih model yang menghasilkan uji root mean square error terendah.
Sumber daya tambahan
Tutorial berikut memberikan pengenalan tentang Regresi Ridge dan Regresi Lasso:
Tutorial berikut menjelaskan cara melakukan kedua jenis regresi di R dan Python: