Cara menafsirkan nilai log-likehood (dengan contoh)

Nilai log kemungkinan suatu model regresi merupakan salah satu cara untuk mengukur goodness of fit suatu model. Semakin tinggi nilai log-likelihood, semakin baik model tersebut cocok dengan kumpulan data.

Nilai log kemungkinan untuk model tertentu dapat berkisar dari tak terhingga negatif hingga tak terhingga positif. Nilai kemungkinan log aktual untuk model tertentu umumnya tidak ada artinya, namun berguna untuk membandingkan dua model atau lebih .

Dalam praktiknya, kami sering kali memasukkan beberapa model regresi ke kumpulan data dan memilih model dengan nilai log-likelihood tertinggi sebagai model yang paling sesuai dengan data.

Contoh berikut menunjukkan cara menafsirkan nilai log-likelihood untuk model regresi yang berbeda dalam praktiknya.

Contoh: Menafsirkan nilai log-likelihood

Katakanlah kita memiliki kumpulan data berikut yang menunjukkan jumlah kamar tidur, jumlah kamar mandi, dan harga jual 20 rumah berbeda di lingkungan tertentu:

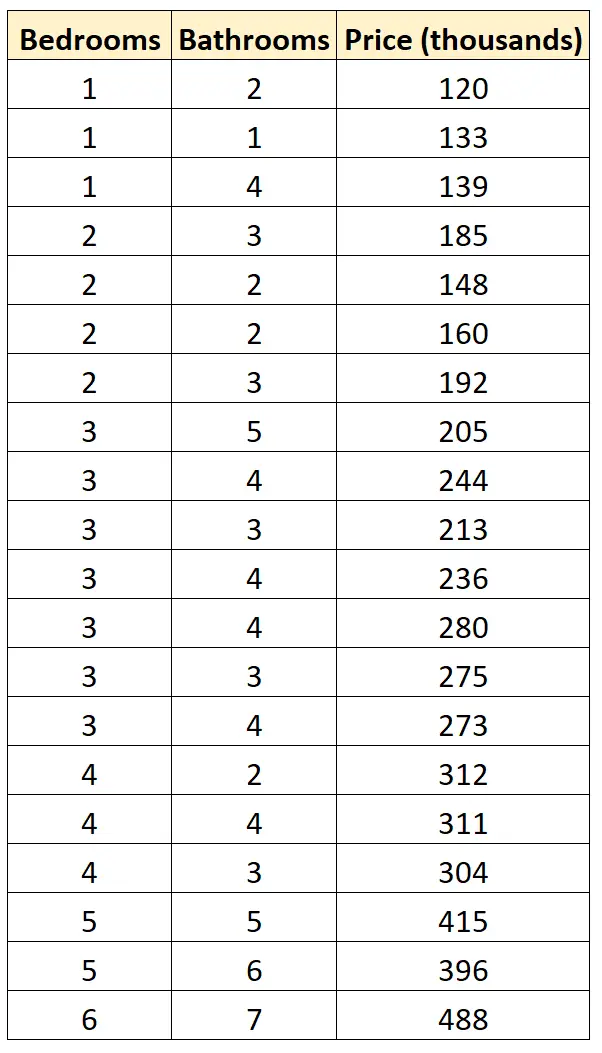
Misalkan kita ingin menyesuaikan dua model regresi berikut dan menentukan model mana yang paling sesuai dengan data:

Model 1 : Harga = β ₀ + β ₁ (jumlah kamar)

Model 2 : Harga = β ₀ + β ₁ (jumlah kamar mandi)

Kode berikut menunjukkan cara menyesuaikan setiap model regresi dan menghitung nilai log-likelihood setiap model di R:

 #define data
df <- data. frame (beds=c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
                        3, 3, 3, 3, 4, 4, 4, 5, 5, 6),
                 baths=c(2, 1, 4, 3, 2, 2, 3, 5, 4, 3,
                         4, 4, 3, 4, 2, 4, 3, 5, 6, 7),
                 price=c(120, 133, 139, 185, 148, 160, 192, 205, 244, 213,
                         236, 280, 275, 273, 312, 311, 304, 415, 396, 488))

#fitmodels
model1 <- lm(price~beds, data=df)
model2 <- lm(price~baths, data=df)

#calculate log-likelihood value of each model
logLik(model1)

'log Lik.' -91.04219 (df=3)

logLik(model2)

'log Lik.' -111.7511 (df=3)

Model pertama memiliki nilai log kemungkinan yang lebih tinggi ( -91.04 ) dibandingkan model kedua ( -111.75 ), yang berarti model pertama memberikan kesesuaian yang lebih baik dengan data.

Tindakan pencegahan untuk menggunakan nilai kemungkinan log

Saat menghitung nilai kemungkinan log, penting untuk diperhatikan bahwa menambahkan variabel prediktor tambahan ke model hampir selalu meningkatkan nilai kemungkinan log, meskipun variabel prediktor tambahan tersebut tidak signifikan secara statistik.

Artinya Anda hanya boleh membandingkan nilai log kemungkinan antara dua model regresi jika setiap model memiliki jumlah variabel prediktor yang sama.

Untuk membandingkan model dengan jumlah variabel prediktor yang berbeda, Anda dapat melakukan uji rasio kemungkinan untuk membandingkan kesesuaian dua model regresi bertingkat.

Sumber daya tambahan

Cara menggunakan fungsi lm() agar sesuai dengan model linier di R
Cara melakukan uji rasio kemungkinan di R