Distribusi multinomial
Artikel ini menjelaskan apa itu distribusi multinomial dalam statistik. Jadi, Anda akan menemukan definisi distribusi multinomial, apa rumusnya, latihan yang diselesaikan, dan apa saja properti dari jenis distribusi probabilitas ini. Selain itu, Anda dapat menghitung probabilitas distribusi multinomial dengan kalkulator online.
Apa itu distribusi multinomial?
Distribusi multinomial (atau distribusi multinomial ) adalah distribusi probabilitas yang menggambarkan probabilitas beberapa peristiwa yang saling eksklusif terjadi beberapa kali setelah beberapa kali percobaan.
Artinya, jika suatu eksperimen acak dapat menghasilkan tiga atau lebih peristiwa eksklusif dan probabilitas setiap peristiwa terjadi secara terpisah diketahui, maka distribusi multinomial digunakan untuk menghitung probabilitas bahwa ketika beberapa eksperimen dilakukan, sejumlah peristiwa tertentu akan terjadi. waktu setiap saat.
Oleh karena itu, distribusi multinomial merupakan generalisasi dari distribusi binomial.
Rumus distribusi multinomial
Untuk menghitung probabilitas distribusi multinomial, pertama-tama Anda harus menentukan hasil bagi antara faktorial jumlah total data dan faktorial jumlah kemunculan setiap peristiwa, dan hasilnya dikalikan dengan produk probabilitas setiap peristiwa. dibawa ke jumlah kemunculan peristiwa tersebut.
Dengan kata lain rumus distribusi multinomial adalah sebagai berikut:

Emas:
-
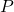
adalah probabilitas distribusi multinomial yang dihitung.
-

adalah jumlah total tes yang dilakukan.
-

adalah berapa kali peristiwa itu terjadi

.
-

adalah kemungkinan terjadinya peristiwa tersebut

.
👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung peluang suatu variabel yang mengikuti distribusi multinomial.
Contoh Distribusi Multinomial
Untuk menyelesaikan pemahaman konsep distribusi multinomial, di bawah ini Anda telah menyelesaikan contoh penghitungan probabilitas distribusi multinomial.
- Sebuah toko menjual tiga produk berbeda. Ketika seorang pelanggan melakukan pembelian, peluang terambilnya produk A, produk B, atau produk C berturut-turut adalah 30%, 15%, dan 55%. Tentukan peluang toko tersebut menjual 8 unit, 2 unit produk A, 1 unit produk B, dan 5 unit produk C.
Masalah yang didefinisikan diatur oleh distribusi multinomial, oleh karena itu perlu diterapkan rumus untuk distribusi probabilitas jenis ini:
![]()
Jadi kami mengganti data dari soal ke dalam rumus dan melakukan perhitungan probabilitas:
![]()
Jadi kemungkinan terjadinya apa yang dinyatakan dalam rumusan masalah adalah 11,4%.
Kalkulator Distribusi Multinomial
Tuliskan banyaknya kemunculan setiap kejadian pada kotak pertama dan, dengan urutan yang sama, peluang terjadinya setiap kejadian pada kotak kedua. Kemudian masukkan jumlah total percobaan yang dilakukan pada ruang kosong terakhir.
Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.
Sifat-sifat distribusi multinomial
Distribusi multinomial memiliki ciri-ciri sebagai berikut:
- Dalam distribusi multinomial, nilai yang diharapkan dari berapa kali kejadian i terjadi ketika menjalankan n percobaan sama dengan jumlah total percobaan yang dilakukan dikalikan dengan probabilitas terjadinya peristiwa tersebut.
![]()
- Dalam distribusi multinomial, varians kejadian i dihitung menggunakan ekspresi berikut:
![]()
- Demikian pula, kovarians antara dua kejadian setara dengan hasil kali jumlah percobaan dikalikan dengan probabilitas tiap kejadian dikalikan -1:
![]()
- Fungsi pembangkit momen untuk distribusi multinomial adalah: