Cara menghitung varians dari distribusi probabilitas
Distribusi probabilitas memberi tahu kita probabilitas suatu variabel acak mengambil nilai tertentu.
Misalnya, distribusi probabilitas berikut memberi tahu kita probabilitas bahwa tim sepak bola tertentu akan mencetak sejumlah gol dalam pertandingan tertentu:

Untuk mencari varians suatu distribusi probabilitas, kita dapat menggunakan rumus berikut:
σ 2 = Σ( xi -μ) 2 * P( xi )
Emas:
- x i : Nilai ke-i
- μ: Rata-rata distribusi
- P(x i ) : Probabilitas nilai ke-i
Misalnya, pertimbangkan distribusi probabilitas kami untuk tim sepak bola:

Jumlah rata-rata gol tim sepak bola akan dihitung sebagai berikut:
μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 gol.
Kami kemudian dapat menghitung variansnya sebagai berikut:
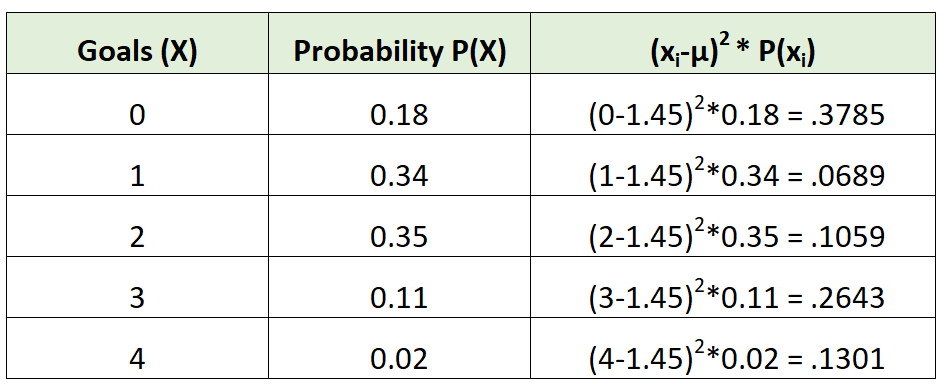
Varians hanyalah jumlah dari nilai-nilai di kolom ketiga. Jadi, kami akan menghitungnya sebagai berikut:
σ2 = 0,3785 + 0,0689 + 0,1059 + 0,2643 + 0,1301 = 0,9475
Contoh berikut menunjukkan cara menghitung varians distribusi probabilitas dalam beberapa skenario lainnya.
Contoh 1: Variasi kerusakan kendaraan
Distribusi probabilitas berikut memberi tahu kita probabilitas bahwa suatu kendaraan akan mengalami sejumlah kegagalan baterai selama periode 10 tahun:
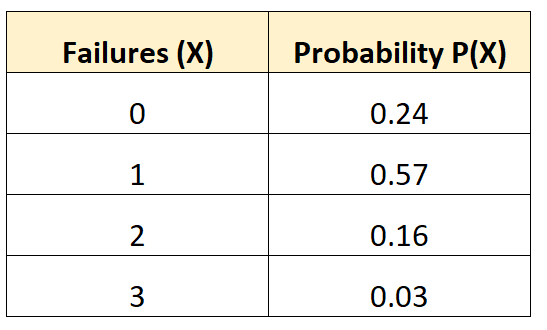
Untuk mencari varians dari distribusi probabilitas ini, pertama-tama kita perlu menghitung jumlah rata-rata kegagalan yang diharapkan:
μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 kegagalan.
Kami kemudian dapat menghitung variansnya sebagai berikut:
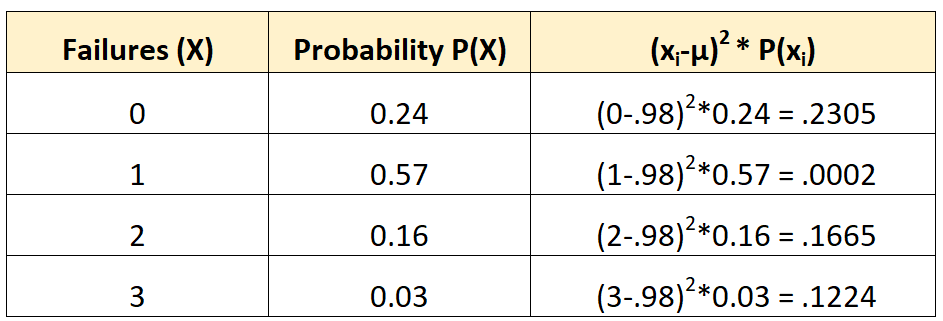
Variansnya adalah jumlah nilai pada kolom ketiga. Jadi, kami akan menghitungnya sebagai berikut:
σ2 = 0,2305 + 0,0002 + 0,1665 + 0,1224 = 0,5196
Contoh 2: Variasi penjualan
Distribusi probabilitas berikut memberi tahu kita probabilitas bahwa penjual tertentu akan menghasilkan sejumlah penjualan tertentu pada bulan mendatang:
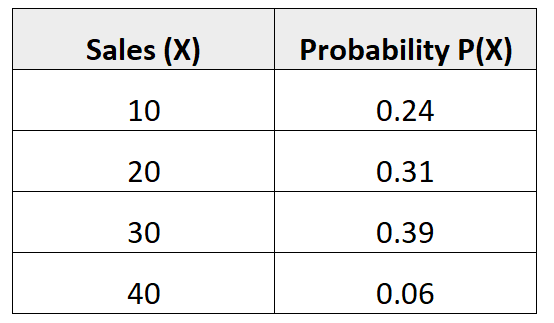
Untuk mencari varians dari distribusi probabilitas ini, pertama-tama kita perlu menghitung jumlah rata-rata penjualan yang diharapkan:
μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 kotor.
Kami kemudian dapat menghitung variansnya sebagai berikut:
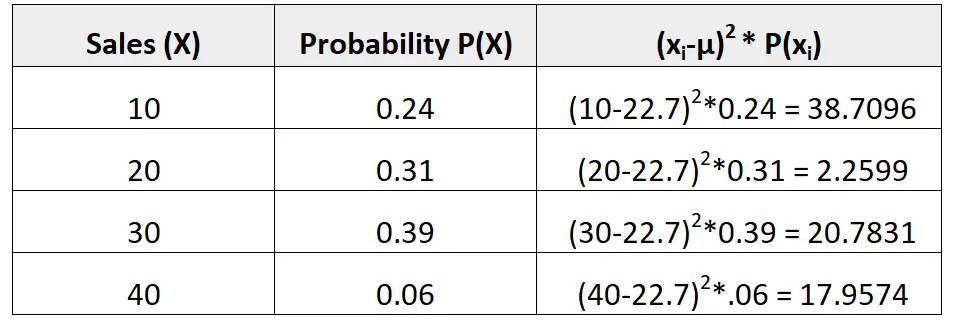
Variansnya adalah jumlah nilai pada kolom ketiga. Jadi, kami akan menghitungnya sebagai berikut:
σ2 = 38,7096 + 2,2599 + 20,7831 + 17,9574 = 79,71
Perhatikan bahwa kita juga dapat menggunakan kalkulator distribusi probabilitas untuk menghitung varians distribusi ini secara otomatis:
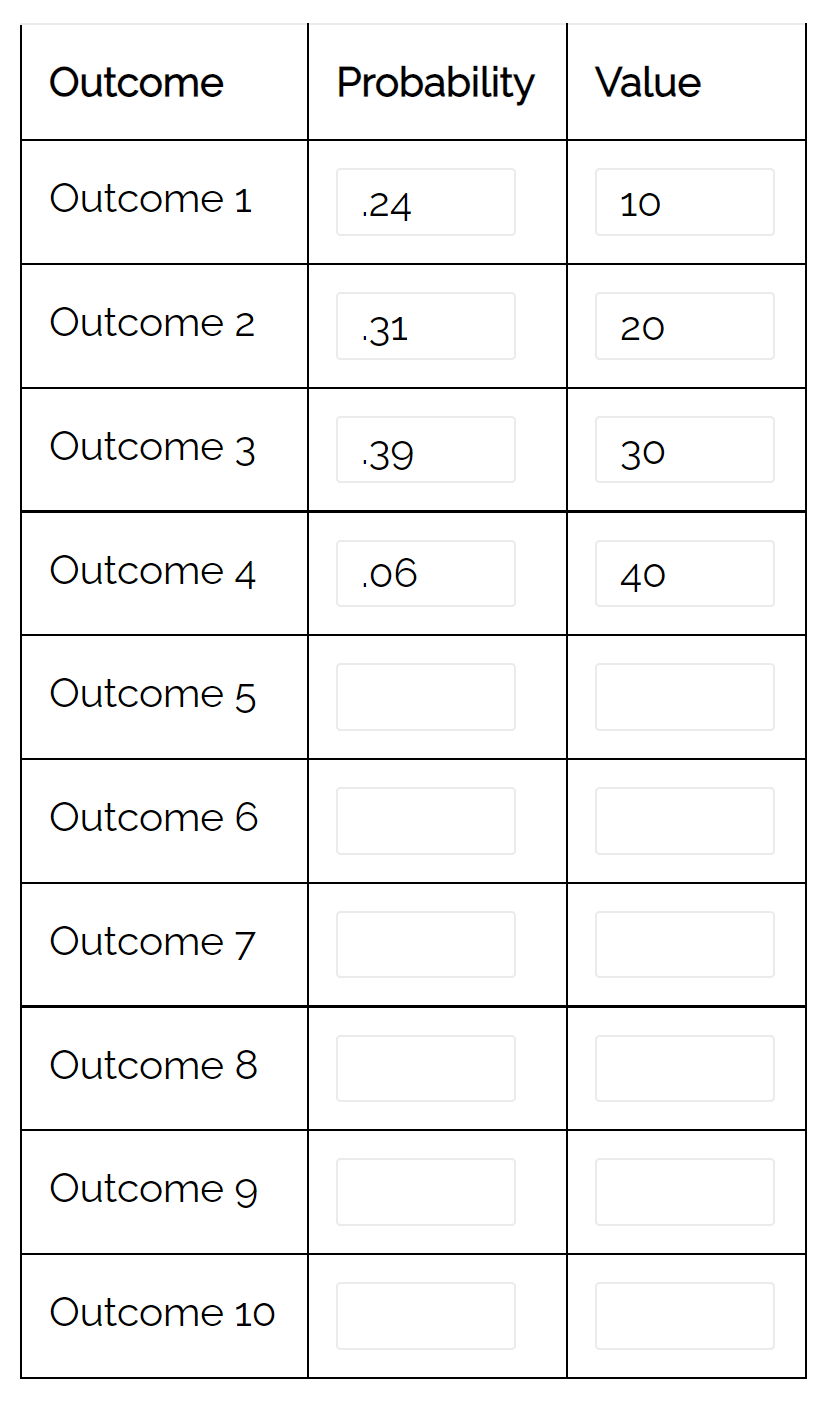

Selisihnya adalah 79,71 . Ini sesuai dengan nilai yang kami hitung secara manual.