Distribusi beta

Oleh Benjamin anderson Agustus 4, 2023 Kemungkinan 0 Komentar

Artikel ini menjelaskan apa itu distribusi beta dan kegunaannya. Demikian pula, Anda akan dapat melihat grafik distribusi beta dan properti dari jenis distribusi probabilitas ini.

Apa distribusi beta?

Distribusi beta adalah distribusi probabilitas yang ditentukan pada interval (0,1) dan diparameterisasi oleh dua parameter positif: α dan β. Dengan kata lain, nilai distribusi beta bergantung pada parameter α dan β.

Oleh karena itu, ciri utama distribusi beta adalah bentuknya dapat dikontrol oleh parameter α dan β. Selain itu, distribusi beta digunakan untuk mendefinisikan variabel acak yang nilainya antara 0 dan 1.

Ada beberapa notasi untuk menunjukkan bahwa variabel acak kontinu diatur oleh distribusi beta, yang paling umum adalah:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}$

Secara statistik, distribusi beta memiliki penerapan yang sangat bervariasi. Misalnya, distribusi beta digunakan untuk mempelajari variasi persentase dalam sampel yang berbeda. Demikian pula dalam manajemen proyek, distribusi beta digunakan untuk melakukan analisis Pert.

Plot distribusi beta

Mengingat definisi distribusi beta, fungsi kepadatan dan fungsi distribusi probabilitas dari distribusi beta diplot di bawah ini.

Di bawah ini Anda dapat melihat bagaimana grafik fungsi kepadatan distribusi beta bervariasi tergantung pada parameter α dan β.

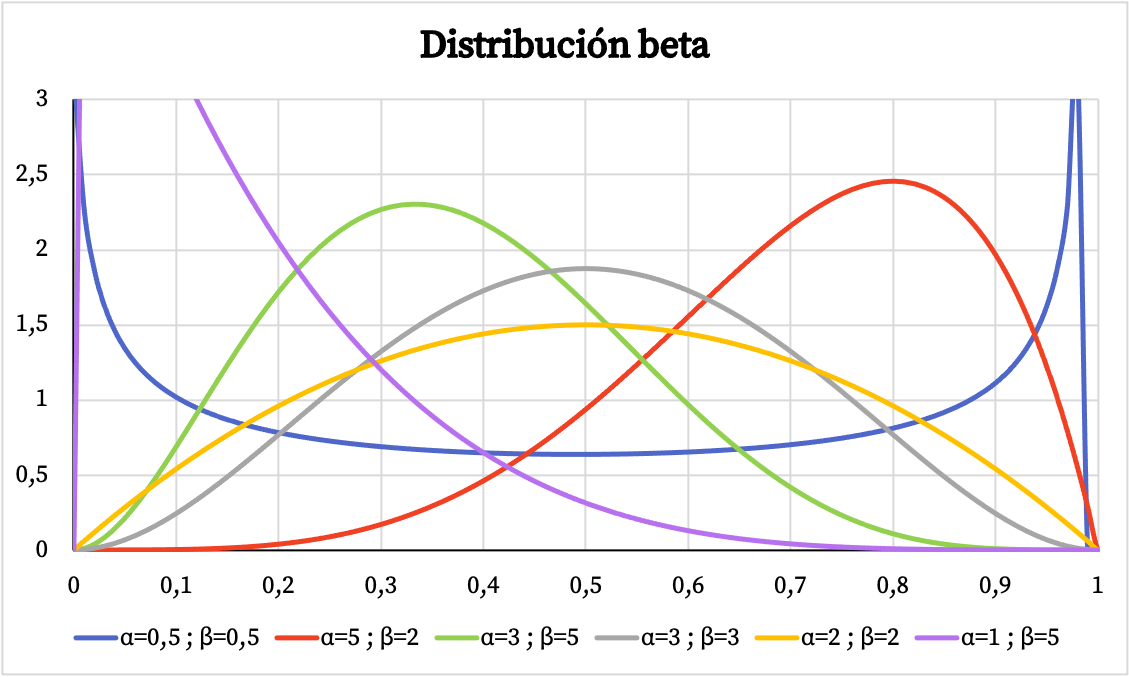
Demikian pula, di bawah ini Anda dapat melihat representasi grafis dari probabilitas kumulatif distribusi beta berdasarkan parameter α dan β.

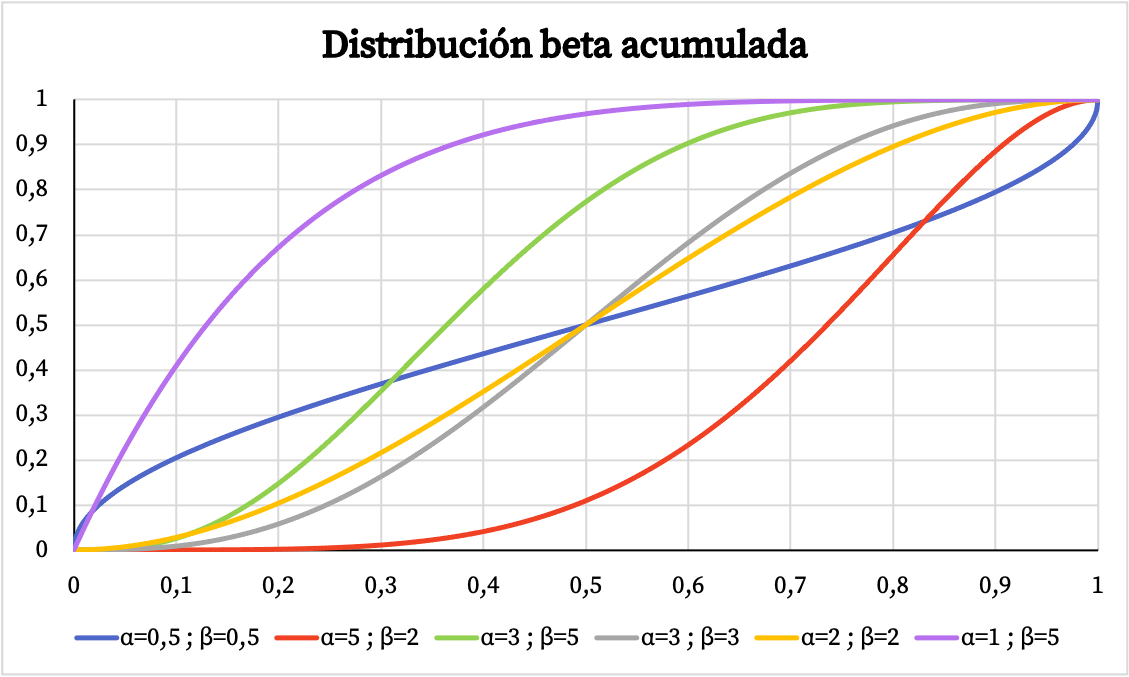
Karakteristik distribusi beta

Di bagian ini kita akan melihat karakteristik terpenting dari distribusi beta.

Parameter α dan β dari distribusi beta adalah bilangan real dan positif.

$\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”44″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Domain distribusi beta berkisar dari 0 hingga 1, dua ekstrem tidak termasuk.</li> </ul> <p class=$ $x\in (0,1)$

Rata-rata distribusi beta sama dengan alpha dibagi dengan jumlah alpha ditambah beta.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}$

Varians distribusi beta dapat dihitung dengan menggunakan rumus berikut:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}$

Untuk nilai alpha dan beta lebih besar dari 1, mode distribusi beta dapat dengan mudah ditemukan dengan ekspresi berikut:

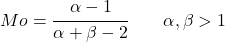
$Mo=\cfrac{\alpha-1}{\alpha+\beta-2}\qquad \alpha,\beta>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”225″ style=”vertical-align: -16px;”></p> </p> <ul> <li> Fungsi kepadatan distribusi beta adalah sebagai berikut:</li> </ul> <p class=$ $\displaystyle P[X=x]=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$

Dimana B(α,β) adalah fungsi beta, yang didefinisikan sebagai:

$\displaystyle B(\alpha,\beta)=\int_0^1x^{\alpha-1}(1-x)^{\beta-1}dx$

Fungsi probabilitas kumulatif dari distribusi beta adalah:

$\displaystyle P[X\leq x]=\frac{B(x;\alpha,\beta)}{B(\alpha,\beta)}$

Dimana B(x;α,β) adalah fungsi beta tidak lengkap, didefinisikan sebagai:

$\displaystyle B(x;\,a,b) = \int_0^x t^{a-1}\,(1-t)^{b-1}\,dt$

Jika X adalah variabel yang ditentukan oleh distribusi beta, maka 1-X adalah variabel yang ditentukan oleh distribusi beta yang parameter alfa dan beta masing-masing merupakan parameter beta dan alfa dari distribusi beta asli.

$X\sim B(\alpha,\beta) \ \color{orange}\bm{\longrightarrow}\color{black} \ 1-X\sim B(\beta,\alpha)$

Jika parameter alfa dan beta pada distribusi beta sama-sama sama dengan 1, maka distribusi tersebut ekuivalen dengan distribusi seragam parameter 0 dan 1.

$X\sim B(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim U(0,1)$

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Apa distribusi beta?

Plot distribusi beta

Karakteristik distribusi beta

Tentang Penulis

Benjamin anderson

Tambahkan komentar