Cara menguji normalitas di r (4 metode)

Banyak uji statistik mengasumsikan bahwa kumpulan data terdistribusi normal.

Ada empat cara umum untuk memeriksa asumsi ini di R:

1. (Metode visual) Membuat histogram.

• Jika histogram kira-kira berbentuk “lonceng”, maka data diasumsikan terdistribusi normal.

2. (Metode visual) Buat plot QQ.

• Jika titik-titik pada plot terletak kira-kira sepanjang garis lurus diagonal, maka data diasumsikan berdistribusi normal.

3. (Uji statistik formal) Lakukan uji Shapiro-Wilk.

• Jika p-value uji lebih besar dari α = 0,05 maka data diasumsikan berdistribusi normal.

4. (Uji statistik formal) Lakukan uji Kolmogorov-Smirnov.

• Jika p-value uji lebih besar dari α = 0,05 maka data diasumsikan berdistribusi normal.

Contoh berikut menunjukkan cara menggunakan masing-masing metode ini dalam praktik.

Metode 1: Buat Histogram

Kode berikut menunjukkan cara membuat histogram untuk dataset yang terdistribusi normal dan tidak terdistribusi normal di R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

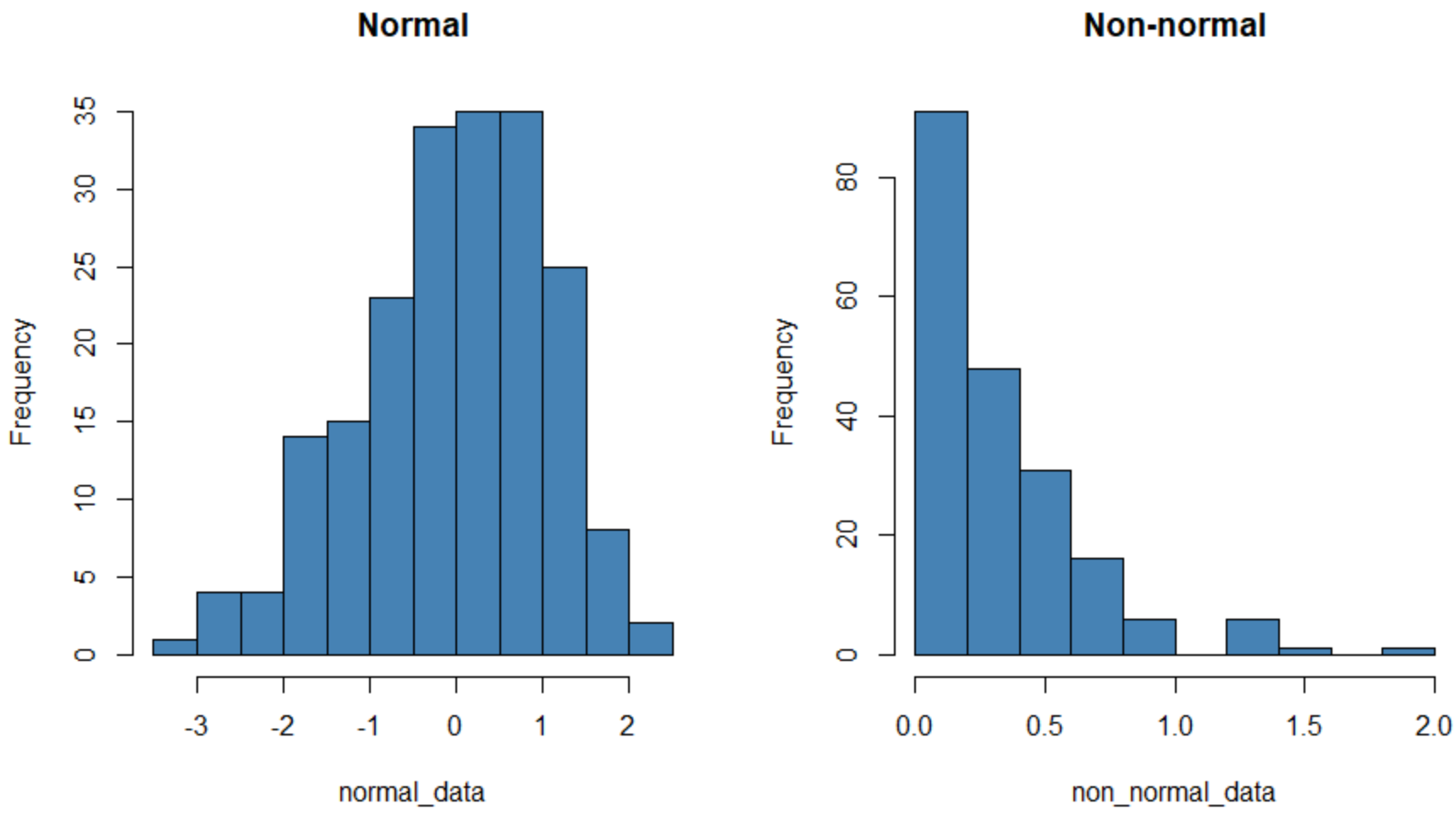
Histogram di sebelah kiri menunjukkan kumpulan data yang berdistribusi normal (kira-kira berbentuk “lonceng”) dan histogram di sebelah kanan menunjukkan kumpulan data yang tidak berdistribusi normal.

Metode 2: Buat Plot QQ

Kode berikut menunjukkan cara membuat plot QQ untuk kumpulan data yang terdistribusi normal dan tidak terdistribusi normal di R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

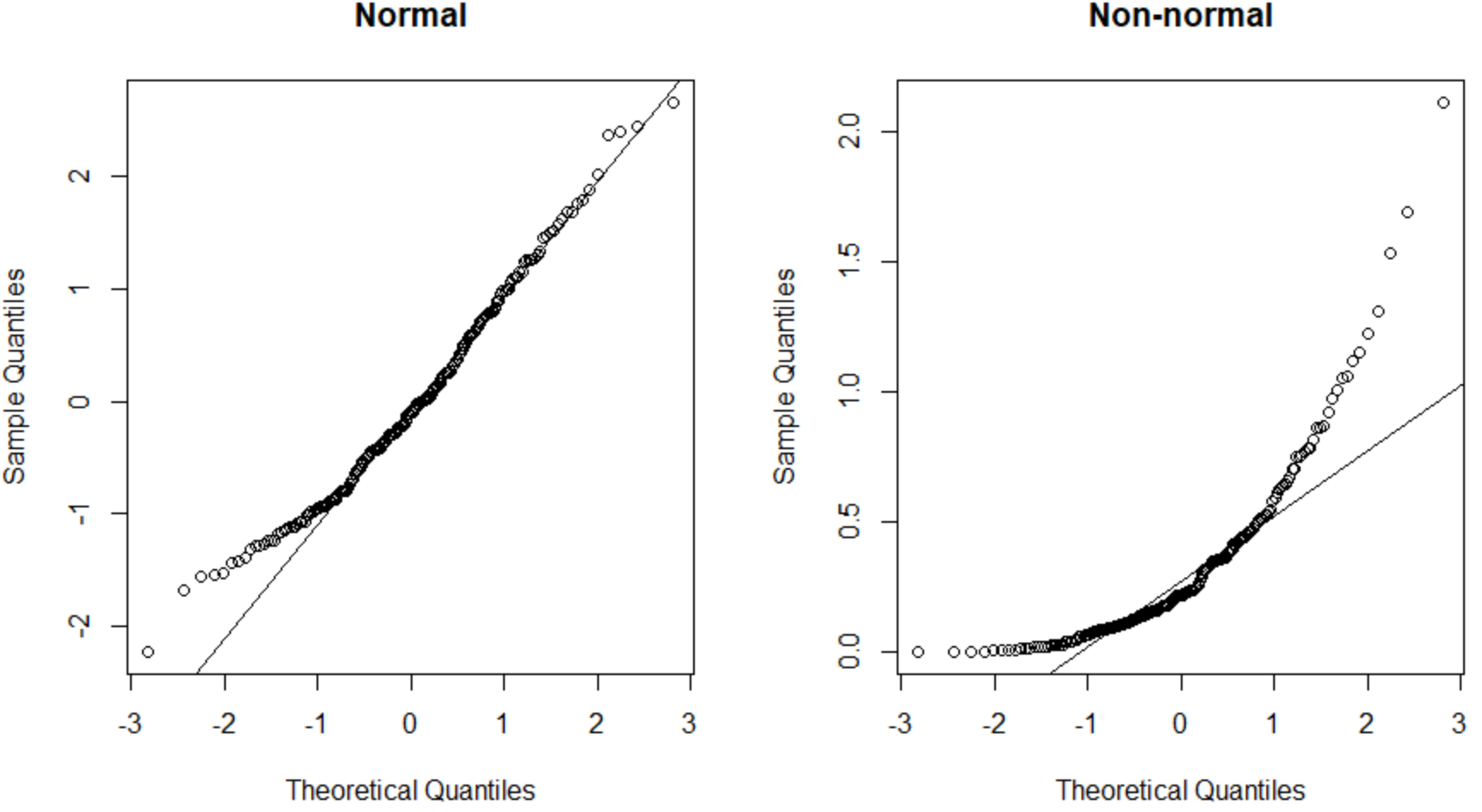
Plot QQ di sebelah kiri menyajikan kumpulan data yang berdistribusi normal (titik-titiknya terletak pada garis diagonal lurus) dan plot QQ di sebelah kanan menyajikan kumpulan data yang tidak berdistribusi normal.

Metode 3: Lakukan tes Shapiro-Wilk

Kode berikut menunjukkan cara melakukan pengujian Shapiro-Wilk pada kumpulan data yang terdistribusi normal dan tidak terdistribusi normal di R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

Nilai p pada pengujian pertama tidak kurang dari 0,05 yang menunjukkan bahwa data berdistribusi normal.

Nilai p pada pengujian kedua kurang dari 0,05 yang menunjukkan bahwa data tidak berdistribusi normal.

Metode 4: Lakukan tes Kolmogorov-Smirnov

Kode berikut menunjukkan cara melakukan pengujian Kolmogorov-Smirnov pada kumpulan data yang terdistribusi normal dan tidak terdistribusi normal di R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

Nilai p pada pengujian pertama tidak kurang dari 0,05 yang menunjukkan bahwa data berdistribusi normal.

Nilai p pada pengujian kedua kurang dari 0,05 yang menunjukkan bahwa data tidak berdistribusi normal.

Cara menangani data yang tidak normal

Jika kumpulan data tertentu tidak terdistribusi normal, kita sering kali dapat melakukan salah satu transformasi berikut untuk membuatnya lebih terdistribusi normal:

1. Transformasi log: ubah nilai x menjadi log(x) .

2. Transformasi akar kuadrat: Ubah nilai x menjadi √x .

3. Transformasi akar pangkat tiga: ubah nilai x menjadi x ^1/3 .

Dengan melakukan transformasi ini, kumpulan data secara umum menjadi lebih terdistribusi secara normal.

Baca tutorial ini untuk melihat cara melakukan transformasi ini di R.

Sumber daya tambahan

Cara membuat histogram di R
Cara membuat dan menafsirkan plot QQ di R
Cara melakukan tes Shapiro-Wilk di R
Cara melakukan tes Kolmogorov-Smirnov di R