Memahami kesalahan standar kemiringan regresi

Kesalahan standar kemiringan regresi adalah cara untuk mengukur “ketidakpastian” dalam memperkirakan kemiringan regresi.

Ini dihitung sebagai berikut:

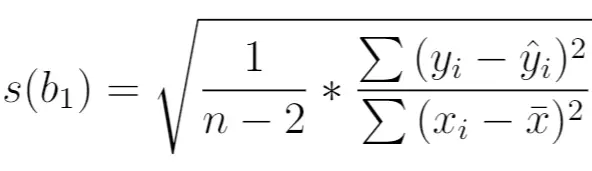
Emas:

• n : jumlah ukuran sampel
• y _i : nilai sebenarnya dari variabel respon
• ŷ _i : nilai prediksi variabel respon
• x _i : nilai riil variabel prediktif
• x̄ : nilai rata-rata variabel prediktif

Semakin kecil kesalahan standarnya, semakin rendah variabilitas di sekitar estimasi koefisien kemiringan regresi.

Kesalahan standar kemiringan regresi akan ditampilkan di kolom “kesalahan standar” pada keluaran regresi sebagian besar perangkat lunak statistik:

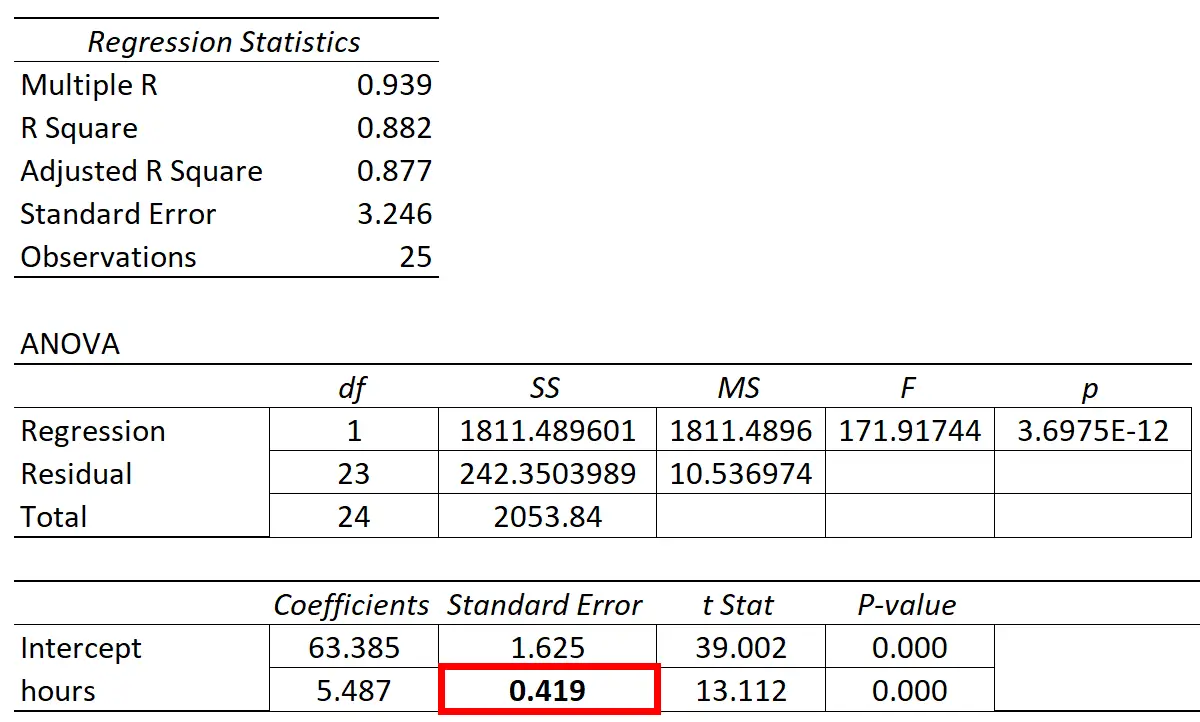
Contoh berikut menunjukkan cara menafsirkan kesalahan standar kemiringan regresi dalam dua skenario berbeda.

Contoh 1: Menafsirkan Kesalahan Standar Kecil pada Kemiringan Regresi

Misalkan seorang profesor ingin memahami hubungan antara jumlah jam belajar dan nilai ujian akhir siswa di kelasnya.

Ini mengumpulkan data untuk 25 siswa dan membuat diagram sebar berikut:

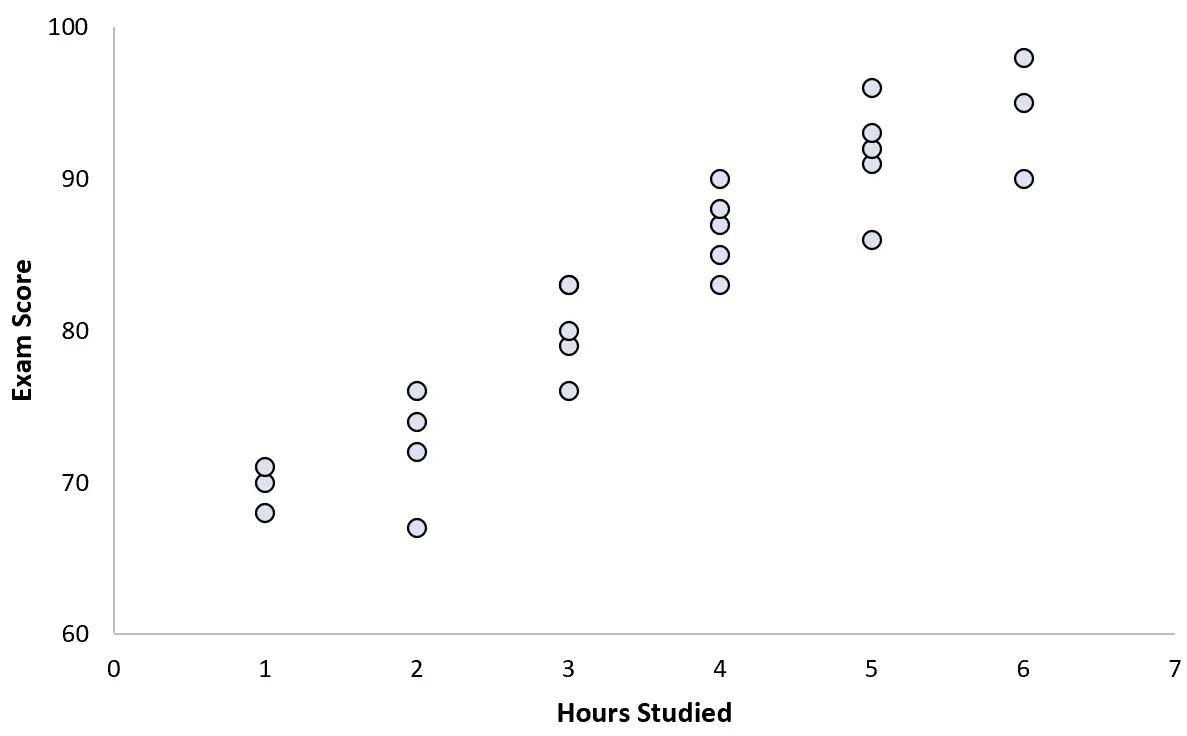
Terdapat hubungan positif yang jelas antara kedua variabel tersebut. Seiring bertambahnya jumlah jam belajar, nilai ujian meningkat pada tingkat yang cukup dapat diprediksi.

Dia kemudian menyesuaikan model regresi linier sederhana dengan menggunakan jam belajar sebagai variabel prediktor dan nilai ujian akhir sebagai variabel respon.

Tabel berikut menunjukkan hasil regresi:

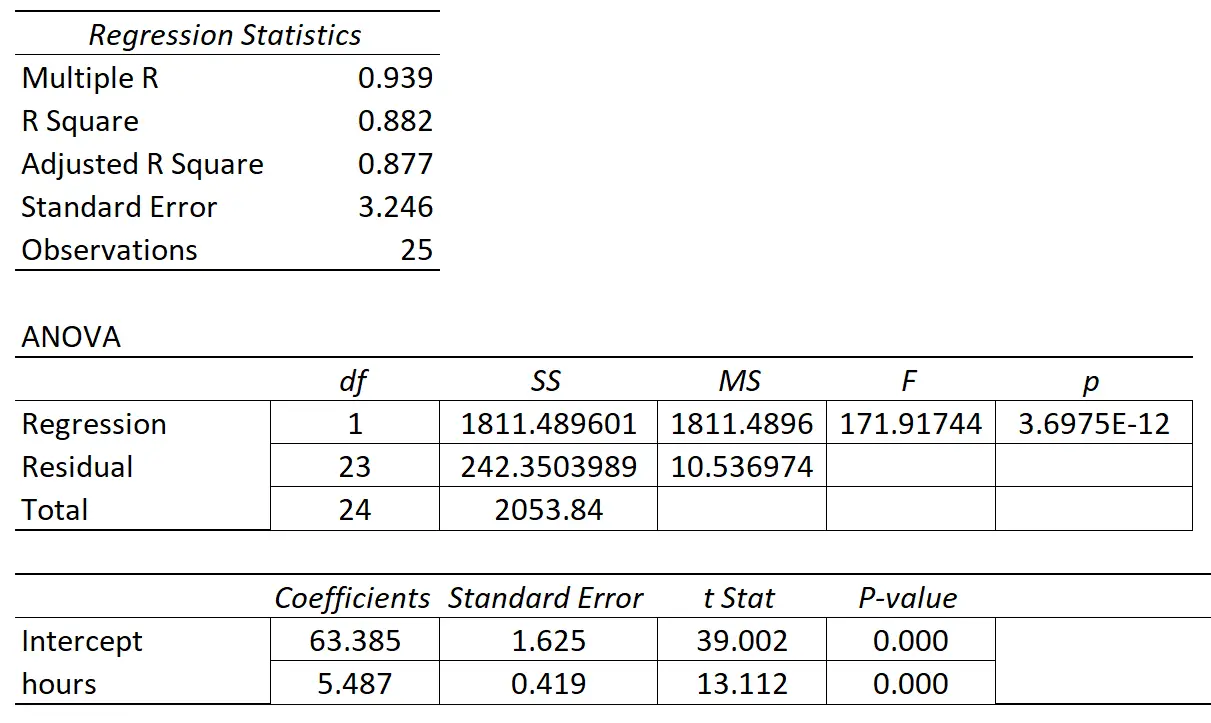
Koefisien variabel prediktor “jam belajar” adalah 5,487. Hal ini menunjukkan bahwa setiap tambahan jam belajar dikaitkan dengan peningkatan rata-rata nilai ujian sebesar 5.487 .

Kesalahan standarnya adalah 0,419 , yang mewakili ukuran variabilitas di sekitar perkiraan kemiringan regresi ini.

Kita dapat menggunakan nilai ini untuk menghitung statistik-t untuk variabel prediktor “jam belajar”:

• t statistik = perkiraan koefisien / kesalahan standar
• t-statistik = 5,487 / 0,419
• t-statistik = 13,112

Nilai p yang sesuai dengan statistik tes ini adalah 0,000, yang menunjukkan bahwa “jam belajar” memiliki hubungan yang signifikan secara statistik dengan nilai ujian akhir.

Karena kesalahan standar kemiringan regresi lebih kecil dibandingkan dengan estimasi koefisien kemiringan regresi, maka variabel prediktor signifikan secara statistik.

Contoh 2: Menafsirkan Kesalahan Standar Besar pada Kemiringan Regresi

Misalkan profesor lain ingin memahami hubungan antara jumlah jam belajar dan nilai ujian akhir siswa di kelasnya.

Dia mengumpulkan data untuk 25 siswa dan membuat diagram sebar berikut:

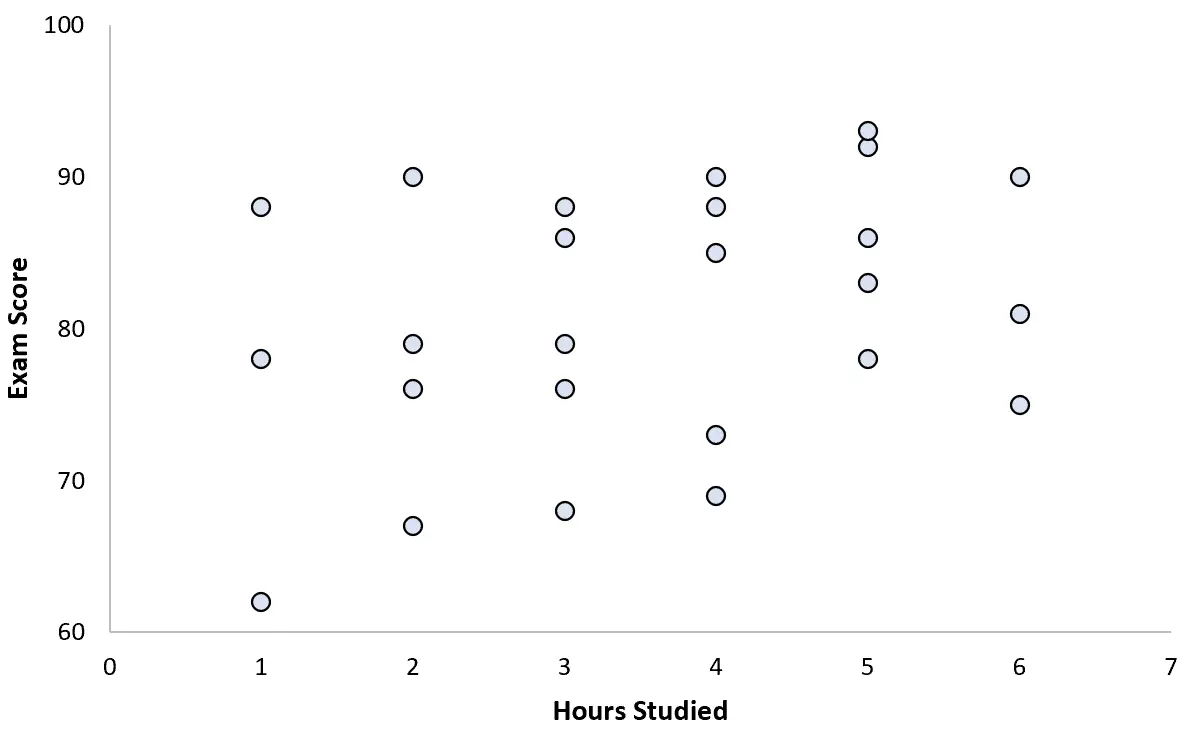
Tampaknya ada sedikit hubungan positif antara kedua variabel tersebut. Seiring bertambahnya jumlah jam belajar, nilai ujian umumnya meningkat, namun tidak pada tingkat yang dapat diprediksi.

Asumsikan profesor tersebut kemudian memasang model regresi linier sederhana dengan menggunakan jam belajar sebagai variabel prediktor dan nilai ujian akhir sebagai variabel respon.

Tabel berikut menunjukkan hasil regresi:

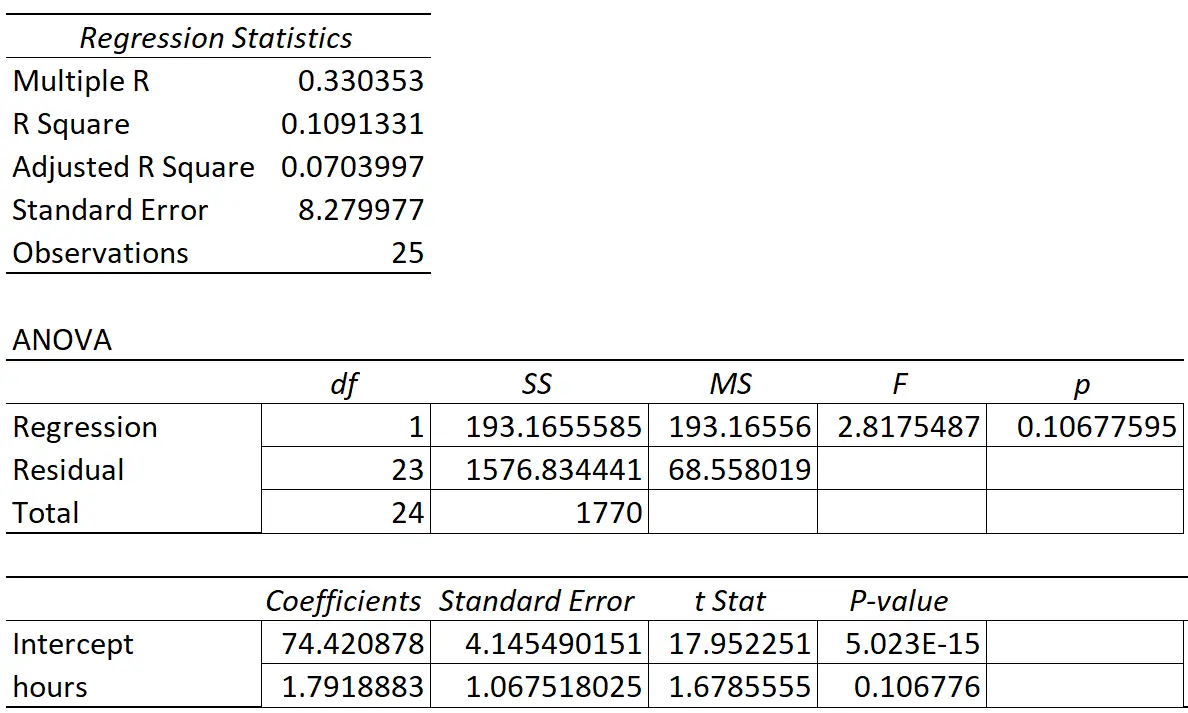
Koefisien variabel prediktor “jam belajar” sebesar 1,7919. Hal ini menunjukkan bahwa setiap tambahan jam belajar dikaitkan dengan peningkatan rata-rata nilai ujian sebesar 1,7919 .

Kesalahan standarnya adalah 1,0675 , yang merupakan ukuran variabilitas di sekitar perkiraan kemiringan regresi ini.

Kita dapat menggunakan nilai ini untuk menghitung statistik-t untuk variabel prediktor “jam belajar”:

• t statistik = perkiraan koefisien / kesalahan standar
• t-statistik = 1,7919 / 1,0675
• t-statistik = 1,678

Nilai p yang sesuai dengan statistik pengujian ini adalah 0,107. Karena nilai p ini tidak kurang dari 0,05, hal ini menunjukkan bahwa “jam belajar” tidak memiliki hubungan yang signifikan secara statistik dengan nilai ujian akhir.

Karena kesalahan standar kemiringan regresi relatif besar terhadap estimasi koefisien kemiringan regresi, maka variabel prediktor tidak signifikan secara statistik.

Sumber daya tambahan

Pengantar Regresi Linier Sederhana
Pengantar Regresi Linier Berganda
Cara Membaca dan Menafsirkan Tabel Regresi