Kapan sebaiknya anda menggunakan plot kotak? (3 skenario)

Plot kotak adalah jenis plot yang menampilkan ringkasan lima digit kumpulan data, yang meliputi:

• Nilai minimum
• Kuartil pertama (persentil ke-25)
• Nilai median
• Kuartil ketiga (persentil ke-75)
• Nilai maksimum

Kami menggunakan tiga langkah sederhana untuk membuat plot kotak untuk kumpulan data apa pun:

• 1. Gambarlah sebuah kotak dari kuartil pertama hingga kuartil ketiga
• 2. Gambarlah garis vertikal di median
• 3. Gambarkan “kumis” kuartil ke nilai minimum dan maksimum

Kami biasanya membuat plot kotak dalam salah satu dari tiga skenario:

Skenario 1: Visualisasikan distribusi nilai dalam kumpulan data.

Plot kotak memungkinkan kita dengan cepat memvisualisasikan distribusi nilai dalam kumpulan data dan melihat di mana letak lima nilai ringkasan numerik.

Skenario 2: Untuk membandingkan dua atau lebih distribusi.

Plot kotak berdampingan memungkinkan kita memvisualisasikan perbedaan antara dua atau lebih distribusi dan membandingkan nilai median dan distribusi nilai antar distribusi.

Skenario 3: Untuk mengidentifikasi outlier.

Dalam plot kotak, outlier biasanya diwakili oleh lingkaran kecil yang melampaui setiap kumis. Suatu observasi dikatakan outlier jika memenuhi salah satu kriteria berikut:

• Pengamatan kurang dari Q1 – 1,5*(Rentang interkuartil)
• Pengamatan lebih besar dari Q3 + 1,5*(Rentang interkuartil)

Dengan membuat plot kotak, kita dapat dengan cepat melihat apakah suatu distribusi memiliki outlier atau tidak.

Contoh berikut menunjukkan bagaimana kita akan menggunakan plot kotak di setiap skenario.

Skenario 1: Visualisasikan distribusi nilai dalam kumpulan data

Misalkan seorang pelatih bola basket ingin memvisualisasikan distribusi poin yang dicetak oleh pemain timnya dan karena itu membuat plot kotak berikut:

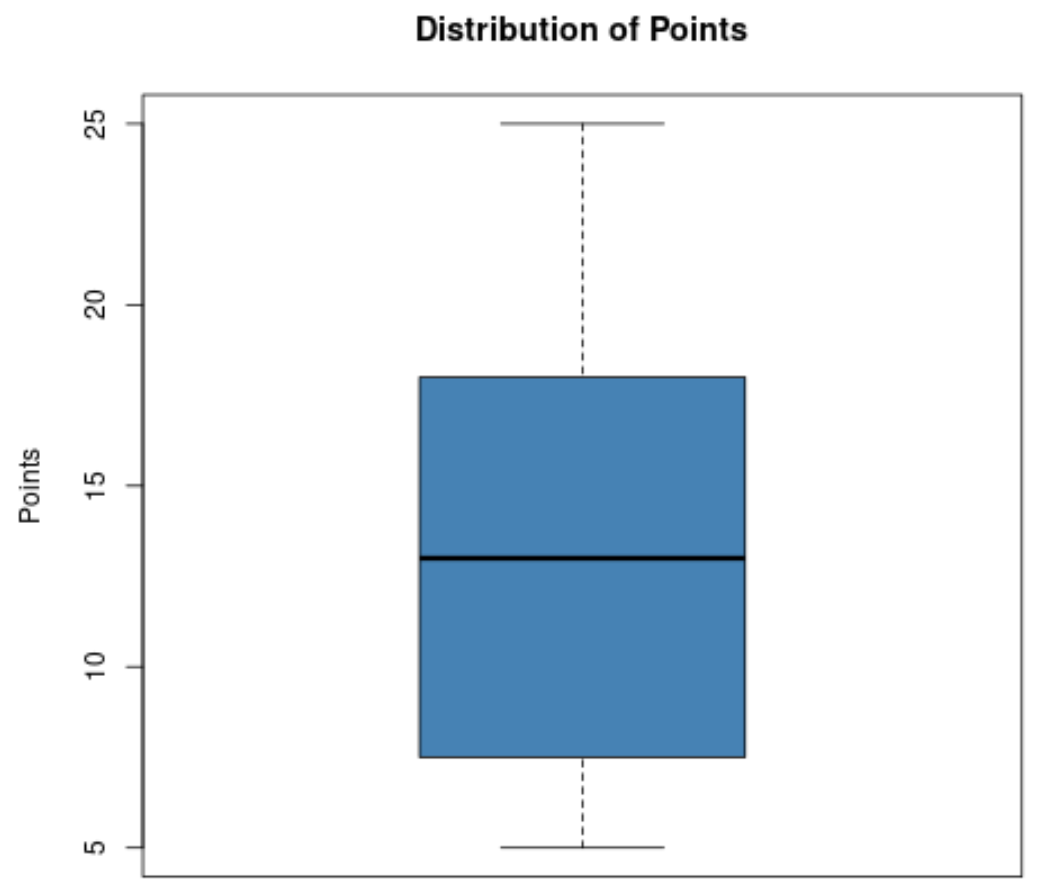
Berdasarkan plot kotak ini, dia dapat dengan cepat melihat nilai berikut:

• Minimal: 5
• T1 (kuartil pertama): kira-kira 8
• Median: sekitar jam 13
• T3 (kuartil ketiga): sekitar 18
• Maksimum: 25

Hal ini memungkinkan pelatih untuk dengan cepat melihat bahwa poin yang dicetak oleh pemain berkisar antara 5 hingga 25, bahwa median poin yang dicetak adalah sekitar 13, dan bahwa 50% pemainnya mencetak antara sekitar 8 dan 18 poin per permainan.

Skenario 2: Bandingkan dua distribusi atau lebih

Misalkan seorang analis olahraga ingin membandingkan distribusi poin yang dicetak oleh pemain bola basket di tiga tim berbeda dan membuat plot kotak berikut:

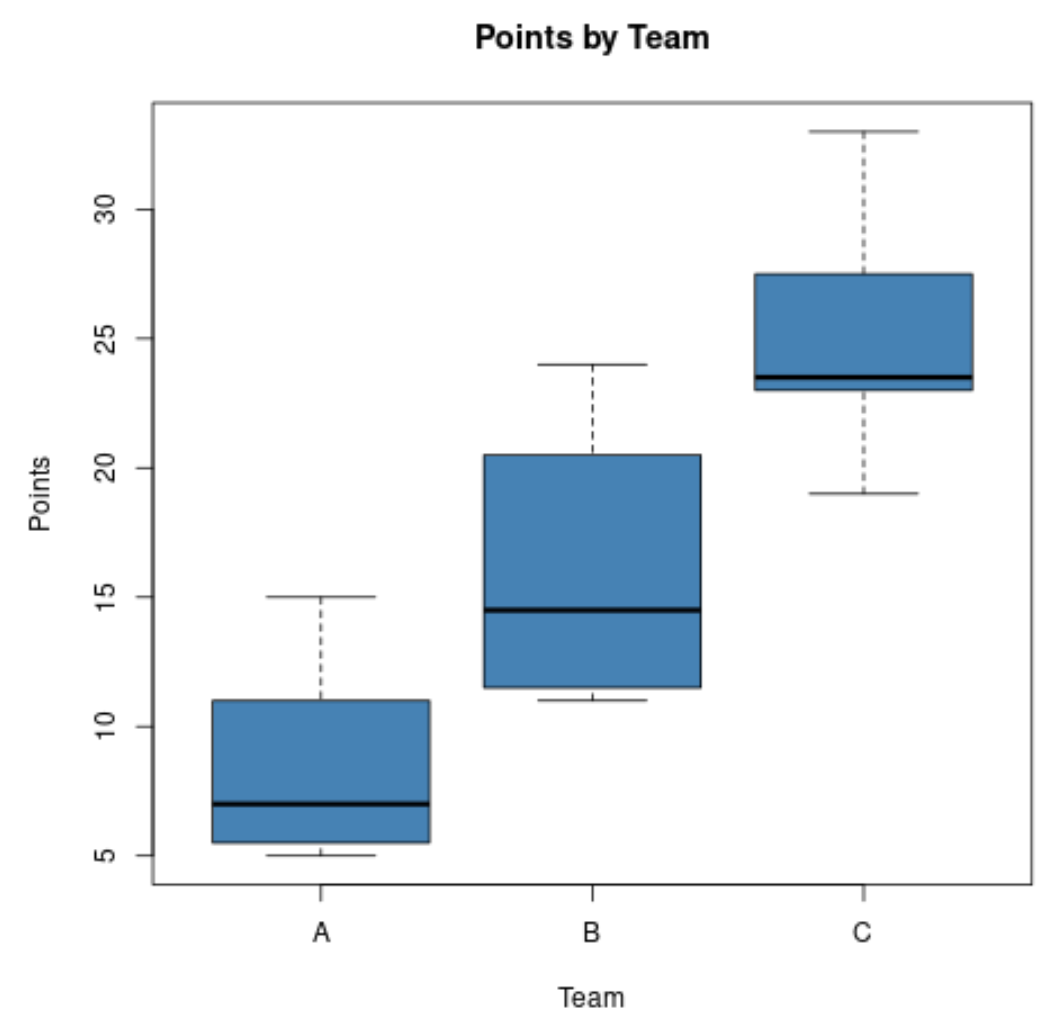
Dengan menggunakan grafik ini, dia dapat dengan cepat melihat bahwa Tim C memiliki skor titik tengah tertinggi dan Tim A memiliki skor titik tengah terendah.

Dia juga dapat dengan cepat melihat bahwa Tim B memiliki distribusi poin terbesar karena plot kotak Tim B memiliki kotak terpanjang.

Skenario 3: Identifikasi outlier

Misalkan seorang pelatih bola basket ingin mengetahui apakah salah satu pemainnya merupakan pemain outlier dalam hal perolehan poin. Dia memutuskan untuk membuat plot kotak berikut untuk memvisualisasikan distribusi poin yang dicetak oleh para pemainnya:

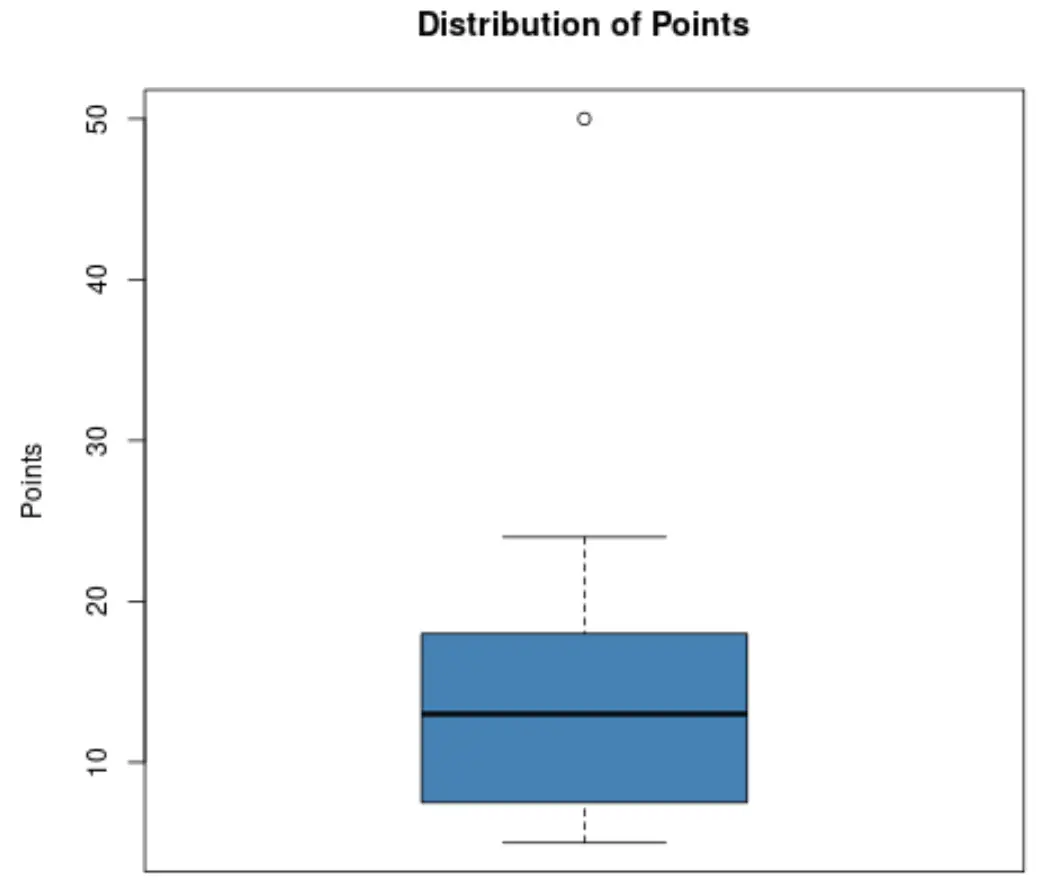
Dengan menggunakan plot ini, pelatih dapat melihat bahwa titik kecil di bagian atas plot menunjukkan adanya outlier.

Secara khusus, salah satu pemain mencetak sekitar 50 poin, yang dianggap outlier dibandingkan dengan semua poin lainnya yang dicetak.

Sumber daya tambahan

Tutorial berikut menawarkan penjelasan mendetail tentang cara menggunakan plot kotak dalam praktik:

Cara Mencari Rentang Interkuartil (IQR) dari Plot Kotak
Cara Mengidentifikasi Asimetri pada Plot Kotak
Bagaimana Membandingkan Plot Kotak

Tutorial berikut menjelaskan cara membuat plot kotak di berbagai perangkat lunak statistik:

Cara Membuat Plot Kotak di Google Sheets
Cara Membuat Plot Kotak di SPSS
Cara Membuat Plot Kotak Berdampingan di Excel
Cara Membuat Plot Kotak Berdampingan di R