Mae vs. rmse: metrik mana yang harus anda gunakan?
Model regresi digunakan untuk mengukur hubungan antara satu atau lebih variabel prediktor dan variabel respon .
Setiap kali kita menyesuaikan model regresi, kita ingin memahami seberapa baik model tersebut mampu menggunakan nilai variabel prediktor untuk memprediksi nilai variabel respon.
Dua metrik yang sering kita gunakan untuk mengukur seberapa cocok suatu model dengan kumpulan data adalah mean absolute error (MAE) dan root mean square error (RMSE), yang dihitung sebagai berikut:
MAE : Metrik yang memberi tahu kita perbedaan absolut rata-rata antara nilai prediksi dan nilai aktual dalam kumpulan data. Semakin rendah MAE, semakin baik model tersebut cocok dengan kumpulan data.
MAE = 1/n * Σ|y saya – ŷ saya |
Emas:
- Σ adalah simbol yang berarti “jumlah”
- y i adalah nilai observasi untuk observasi ke-i
- ŷ i merupakan nilai prediksi pada pengamatan ke i
- n adalah ukuran sampel
RMSE : Metrik yang memberi tahu kita akar kuadrat dari selisih rata-rata akar kuadrat antara nilai prediksi dan nilai sebenarnya dalam kumpulan data. Semakin rendah RMSE, semakin baik model tersebut cocok dengan kumpulan data.
Ini dihitung sebagai berikut:
RMSE = √ Σ(y saya – ŷ saya ) 2 / n
Emas:
- Σ adalah simbol yang berarti “jumlah”
- ŷ i merupakan nilai prediksi pada pengamatan ke i
- y i adalah nilai observasi untuk observasi ke-i
- n adalah ukuran sampel
Contoh: Perhitungan RMSE dan MAE
Misalkan kita menggunakan model regresi untuk memprediksi berapa banyak poin yang akan dicetak oleh 10 pemain dalam permainan bola basket.
Tabel berikut menunjukkan poin yang diprediksi oleh model dibandingkan dengan poin sebenarnya yang dicetak oleh para pemain:

Dengan menggunakan kalkulator MAE, kita dapat menghitung MAE adalah 3,2.
Hal ini memberitahu kita bahwa rata-rata selisih absolut antara nilai yang diprediksi oleh model dan nilai sebenarnya adalah 3,2.
Dengan menggunakan kalkulator RMSE , kita dapat menghitung RMSE sama dengan 4 .
Hal ini menunjukkan bahwa akar kuadrat dari selisih rata-rata kuadrat antara poin yang diprediksi dan poin yang sebenarnya adalah 4.
Perhatikan bahwa setiap metrik memberi kita gambaran tentang perbedaan umum antara nilai prediksi yang dibuat oleh model dan nilai sebenarnya dalam kumpulan data, namun interpretasi setiap metrik sedikit berbeda.
RMSE vs. MAE: Metrik Mana yang Harus Anda Gunakan?
Jika Anda ingin memberi bobot lebih pada observasi yang jauh dari mean (yaitu jika deviasi 20 lebih dari dua kali lebih buruk dari deviasi 10), lebih baik menggunakan RMSE untuk mengukur kesalahan, karena RMSE adalah lebih sensitif terhadap observasi yang lebih jauh dari mean.
Namun jika “offset” pada angka 20 dua kali lebih buruk dari “offset” pada angka 10 maka lebih baik menggunakan MAE.
Untuk menggambarkan hal ini, misalkan kita mempunyai seorang pemain yang jelas-jelas merupakan outlier dalam hal jumlah poin yang dicetak:
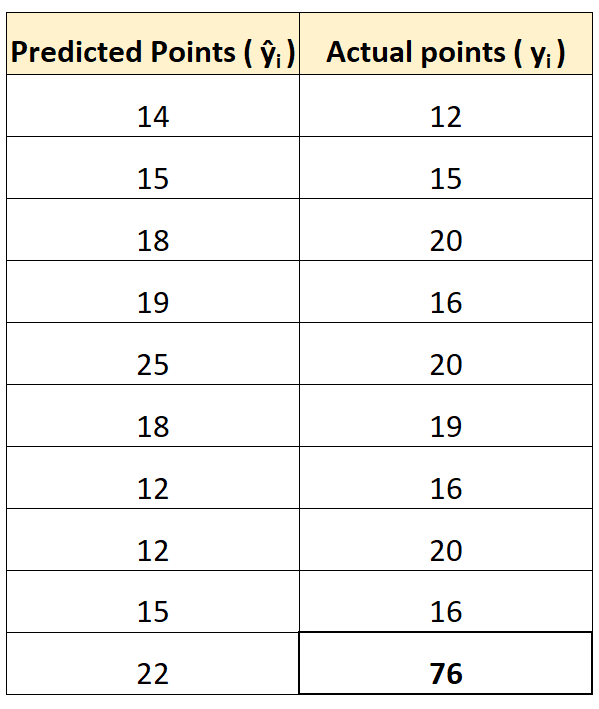
Dengan menggunakan kalkulator online yang disebutkan sebelumnya, kita dapat menghitung MAE dan RMSE sebagai:
- MAE : 8
- RMSE : 16.4356
Perhatikan bahwa RMSE meningkat jauh lebih besar daripada MAE.
Hal ini dikarenakan RMSE menggunakan rumus selisih kuadrat dan selisih kuadrat antara nilai observasi 76 dengan nilai prediksi 22 cukup besar. Hal ini mengakibatkan peningkatan nilai RMSE yang signifikan.
Dalam praktiknya, kami biasanya menyesuaikan beberapa model regresi ke kumpulan data dan hanya menghitung satu metrik ini untuk setiap model.
Misalnya, kita dapat memasukkan tiga model regresi berbeda dan menghitung RMSE untuk setiap model. Kami kemudian akan memilih model dengan nilai RMSE terendah sebagai model “terbaik”, karena model inilah yang membuat prediksi paling dekat dengan nilai sebenarnya dalam kumpulan data.
Apa pun kasusnya, pastikan Anda menghitung metrik yang sama untuk setiap model. Misalnya, jangan menghitung MAE untuk satu model dan RMSE untuk model lain lalu membandingkan kedua pengukuran tersebut.
Sumber daya tambahan
Tutorial berikut menjelaskan cara menghitung MAE menggunakan perangkat lunak statistik yang berbeda:
Cara Menghitung Mean Absolute Error di Excel
Cara menghitung rata-rata kesalahan absolut di R
Cara Menghitung Rata-Rata Kesalahan Absolut dengan Python
Tutorial berikut menjelaskan cara menghitung RMSE menggunakan perangkat lunak statistik yang berbeda:
Cara Menghitung Mean Square Error di Excel
Cara menghitung mean squared error di R
Cara Menghitung Mean Squared Error dengan Python