Memahami uji-t dalam regresi linier
Regresi linier digunakan untuk mengukur hubungan antara variabel prediktor dan variabel respon.
Setiap kali kita melakukan regresi linier, kita ingin mengetahui apakah terdapat hubungan yang signifikan secara statistik antara variabel prediktor dan variabel respon.
Kami menguji signifikansinya dengan melakukan uji-t untuk kemiringan regresi. Kami menggunakan hipotesis nol dan alternatif berikut untuk uji-t ini:
- H 0 : β 1 = 0 (kemiringannya sama dengan nol)
- H A : β 1 ≠ 0 (kemiringan tidak sama dengan nol)
Kami kemudian menghitung statistik uji sebagai berikut:
t = b / SE b
Emas:
- b : estimasi koefisien
- SE b : kesalahan baku estimasi koefisien
Jika nilai p yang sesuai dengan t berada di bawah ambang batas tertentu (misalnya α = 0,05), maka kami menolak hipotesis nol dan menyimpulkan bahwa terdapat hubungan yang signifikan secara statistik antara variabel prediktor dan variabel respons.
Contoh berikut menunjukkan cara melakukan uji-t untuk model regresi linier dalam praktiknya.
Contoh: Menjalankan uji-t untuk regresi linier
Misalkan seorang profesor ingin menganalisis hubungan antara jam belajar dan nilai ujian untuk 40 muridnya.
Ia melakukan regresi linier sederhana dengan menggunakan jam belajar sebagai variabel prediktor dan nilai ujian yang diterima sebagai variabel respon.
Tabel berikut menunjukkan hasil model regresi:
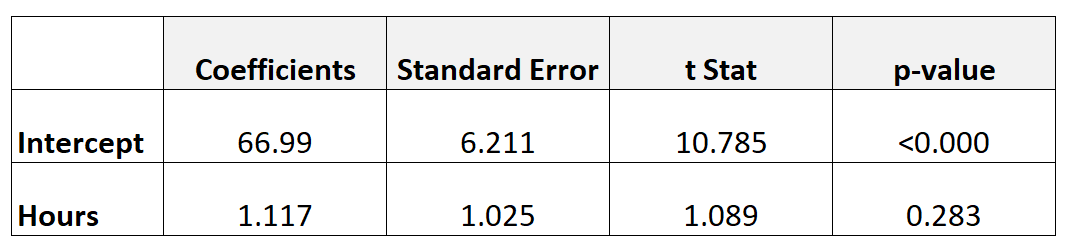
Untuk menentukan apakah jam belajar mempunyai hubungan yang signifikan secara statistik dengan nilai ujian akhir, kita dapat melakukan uji-t.
Kami menggunakan hipotesis nol dan alternatif berikut untuk uji-t ini:
- H 0 : β 1 = 0 (kemiringan jam belajar sama dengan nol)
- H A : β 1 ≠ 0 (kemiringan jam belajar tidak sama dengan nol)
Kami kemudian menghitung statistik uji sebagai berikut:
- t = b / SE b
- t = 1,117 / 1,025
- t = 1,089
Nilai p yang sesuai dengan t = 1,089 dengan df = n-2 = 40 – 2 = 38 adalah 0,283 .
Perhatikan bahwa kita juga dapat menggunakan kalkulator skor T ke nilai P untuk menghitung nilai p ini:
Karena nilai p ini tidak kurang dari 0,05, kita gagal menolak hipotesis nol.
Artinya jam belajar tidak memiliki hubungan yang signifikan secara statistik antara hasil ujian akhir.
Sumber daya tambahan
Tutorial berikut memberikan informasi tambahan tentang regresi linier:
Pengantar Regresi Linier Sederhana
Pengantar Regresi Linier Berganda
Bagaimana menafsirkan koefisien regresi
Bagaimana menafsirkan uji F untuk signifikansi keseluruhan dalam regresi
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya