Apa yang dimaksud dengan akurasi seimbang? (definisi & #038; contoh)

Akurasi seimbang adalah metrik yang dapat kita gunakan untuk mengevaluasi kinerja model klasifikasi .

Ini dihitung sebagai berikut:

Akurasi Seimbang = (Sensitivitas + Spesifisitas) / 2

Emas:

• Sensitivitas : “tingkat positif sebenarnya” – persentase kasus positif yang dapat dideteksi oleh model.
• Kekhususan : “tingkat negatif sebenarnya” – persentase kasus negatif yang dapat dideteksi oleh model.

Metrik ini sangat berguna ketika kedua kelas tidak seimbang, yaitu, satu kelas tampil lebih banyak dibandingkan kelas lainnya.

Contoh berikut menunjukkan cara menghitung akurasi seimbang dalam praktiknya dan menunjukkan mengapa metrik ini sangat berguna.

Contoh: Menghitung Presisi Seimbang

Misalkan seorang analis olahraga menggunakan model regresi logistik untuk memprediksi apakah 400 pemain bola basket perguruan tinggi yang berbeda akan direkrut ke NBA atau tidak.

Matriks konfusi berikut merangkum prediksi yang dibuat oleh model:

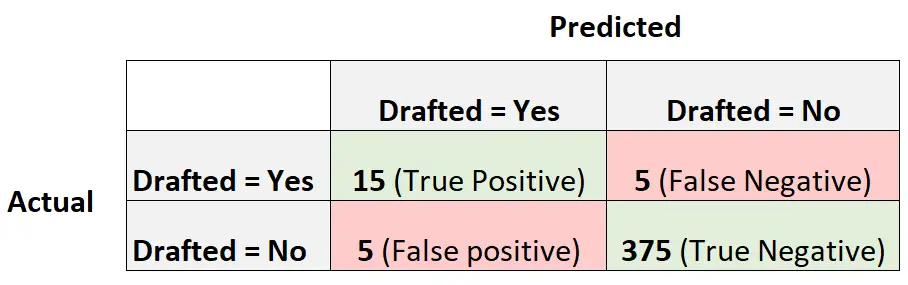
Untuk menghitung akurasi seimbang model, pertama-tama kita akan menghitung sensitivitas dan spesifisitasnya:

• Sensitivitas : “Tingkat positif sebenarnya” = 15 / (15 + 5) = 0,75
• Kekhususan : “Tingkat negatif sebenarnya” = 375 / (375 + 5) = 0,9868

Kami kemudian dapat menghitung presisi seimbang sebagai berikut:

• Akurasi Seimbang = (Sensitivitas + Spesifisitas) / 2
• Akurasi seimbang = (0,75 + 9868) / 2
• Akurasi seimbang = 0,8684

Akurasi seimbang model tersebut ternyata 0,8684 .

Perhatikan bahwa semakin dekat presisi seimbang ke 1, semakin mampu model tersebut mengklasifikasikan observasi dengan benar.

Dalam contoh ini, akurasi yang seimbang cukup tinggi, yang menunjukkan bahwa model regresi logistik mampu memprediksi dengan baik apakah pemain perguruan tinggi akan direkrut ke NBA atau tidak.

Dalam skenario ini, karena kelasnya sangat tidak seimbang (20 pemain direkrut dan 380 pemain tidak), akurasi yang seimbang memberi kita gambaran performa model yang lebih realistis dibandingkan dengan ukuran akurasi keseluruhan.

Misalnya, kami akan menghitung akurasi model sebagai berikut:

• Akurasi = (TP + TN) / (TP + TN + FP + FN)
• Akurasi = (15 + 375) / (15 + 375 + 5 + 5)
• Akurasi = 0,975

Akurasi modelnya adalah 0,975 , yang tampaknya sangat tinggi.

Namun, pertimbangkan model yang hanya memprediksi bahwa setiap pemain tidak akan direkrut. Ini akan memiliki akurasi 380/400 = 0,95 . Ini hanya sedikit lebih rendah dari keakuratan model kami.

Skor akurasi seimbang sebesar 0,8684 memberi kita gambaran yang lebih baik tentang kemampuan model dalam memprediksi kedua kelas.

Dengan kata lain, ini memberi kita gambaran yang lebih baik tentang kemampuan model untuk memprediksi pemain mana yang tidak akan direkrut dan mana yang akan.

Sumber daya tambahan

Tutorial berikut menjelaskan cara membuat matriks konfusi di berbagai perangkat lunak statistik:

Cara Membuat Matriks Kebingungan di Excel
Cara membuat matriks konfusi di R
Cara Membuat Matriks Kebingungan dengan Python