Distribusi lognormal

Oleh Benjamin anderson Agustus 3, 2023 Kemungkinan 0 Komentar

Artikel ini menjelaskan apa itu distribusi lognormal dalam statistik. Jadi, Anda akan mengetahui apa saja sifat-sifat distribusi lognormal dan grafik dari jenis distribusi probabilitas tersebut.

Apa distribusi lognormalnya?

Distribusi lognormal , atau distribusi lognormal , adalah distribusi probabilitas yang mendefinisikan variabel acak yang logaritmanya mengikuti distribusi normal.

Oleh karena itu, jika variabel X berdistribusi normal, maka fungsi eksponensial e ^x berdistribusi lognormal.

$X\sim \text{Lognormal}(\mu,\sigma^2)$

Perhatikan bahwa distribusi lognormal hanya dapat digunakan jika nilai variabelnya positif, karena logaritma adalah fungsi yang hanya mengambil satu argumen positif.

Di antara berbagai penerapan distribusi lognormal dalam statistik, kami membedakan penggunaan distribusi ini untuk menganalisis investasi keuangan dan melakukan analisis keandalan.

Distribusi lognormal dikenal juga sebagai distribusi Tinaut , terkadang juga ditulis sebagai distribusi lognormal atau distribusi log-normal .

Plot distribusi lognormal

Sekarang setelah kita mengetahui definisi distribusi lognormal, pada bagian ini kita akan melihat bagaimana representasi grafis dari distribusi lognormal bervariasi tergantung pada nilai mean aritmatika dan deviasi standarnya.

Grafik fungsi densitas distribusi lognormal adalah sebagai berikut:

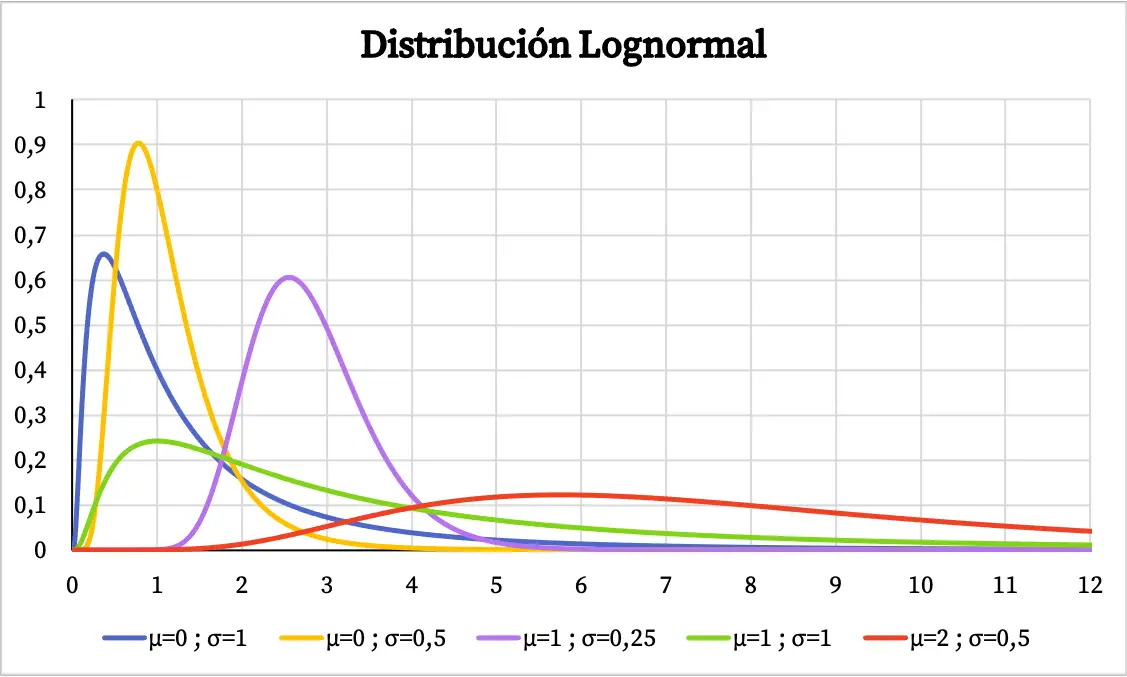
Sedangkan grafik probabilitas kumulatif dari distribusi lognormal adalah sebagai berikut:

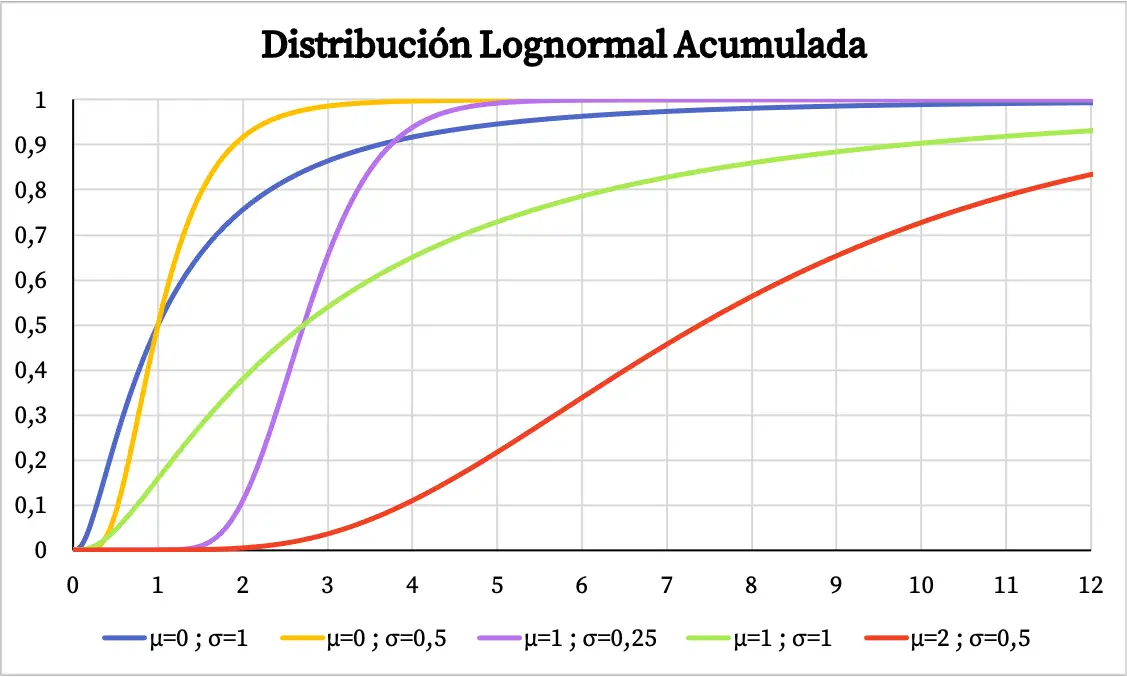
plot probabilitas kumulatif dari distribusi lognormal

Ciri-ciri distribusi lognormal

Distribusi lognormal mempunyai ciri-ciri sebagai berikut:

Distribusi lognormal ditentukan oleh nilai dua parameter, rata-rata aritmatikanya μ dan variansnya σ ² .

$X\sim \text{Lognormal}(\mu,\sigma^2)$

Domain distribusi lognormal terdiri dari bilangan real positif, karena logaritma tidak menerima nilai negatif atau nol.

$x\in (0,+\infty)$

Ekspektasi distribusi lognormal sama dengan angka e yang dipangkatkan dari jumlah mean ditambah varians dibagi dua.

$\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}$

Di sisi lain, varians dari distribusi lognormal dapat dihitung dengan ekspresi berikut:

$Var(X)=\left(e^{\sigma^2}-1\right)\cdot e^{2\mu+\sigma^2$

Modus distribusi lognormal ekuivalen dengan bilangan e yang dipangkatkan ke mean distribusi.

$Mo=e^\mu$

Koefisien skewness distribusi lognormal dapat ditentukan dengan menggunakan rumus berikut:

$\displaystyle A=\left(e^{\sigma^2}+2\right)\cdot\sqrt{e^{\sigma^2}-1}$

Rumus fungsi kepadatan berdistribusi lognormal adalah:

$\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)$

Rumus fungsi probabilitas kumulatif dari distribusi lognormal adalah:

$\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)$

Emas

$\Phi$

adalah fungsi probabilitas kumulatif dari distribusi normal standar .

Rata-rata aritmatika suatu distribusi lognormal lebih besar dari nilai mediannya.

$\mu > Me” title=”Rendered by QuickLaTeX.com” height=”16″ width=”61″ style=”vertical-align: -4px;”></p></p> </div>  <div class=$

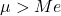
Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Apa distribusi lognormalnya?

Plot distribusi lognormal

Ciri-ciri distribusi lognormal

Tentang Penulis

Benjamin anderson

Tambahkan komentar