Distribusi normal

Oleh Benjamin anderson Agustus 3, 2023 Kemungkinan 0 Komentar

Artikel ini menjelaskan apa itu distribusi normal dalam statistik. Nah, kamu akan mengetahui pengertian distribusi normal, contoh distribusi normal, dan apa saja sifat-sifat distribusi normal.

Berapakah distribusi normalnya?

Distribusi normal adalah distribusi probabilitas kontinu yang grafiknya berbentuk lonceng dan simetris terhadap meannya. Dalam statistika, distribusi normal digunakan untuk memodelkan fenomena dengan karakteristik yang sangat berbeda, oleh karena itu distribusi ini sangat penting.

Faktanya, dalam statistika, distribusi normal sejauh ini dianggap sebagai distribusi yang paling penting dari semua distribusi probabilitas, karena distribusi tersebut tidak hanya dapat memodelkan sejumlah besar fenomena dunia nyata, namun distribusi normal juga dapat digunakan untuk memperkirakan jenis-jenis distribusi probabilitas lainnya. distribusi. dalam kondisi tertentu.

Simbol distribusi normal adalah huruf kapital N. Jadi, untuk menunjukkan bahwa suatu variabel mengikuti distribusi normal, ditandai dengan huruf N dan nilai rata-rata aritmatika dan simpangan bakunya ditambahkan dalam tanda kurung.

$X\sim N(\mu,\sigma)$

Distribusi normal memiliki banyak nama berbeda, antara lain Distribusi Gaussian , Distribusi Gaussian , dan Distribusi Laplace-Gauss .

Contoh Distribusi Normal

Biasanya, kumpulan data yang mengikuti distribusi normal berisi observasi dalam jumlah besar dan mencakup topik yang sangat umum. Di bawah ini beberapa contoh sampel statistik yang secara umum dapat dimodelkan dengan distribusi normal.

Contoh distribusi normal:

Jumlah siswa dalam suatu kursus.
IQ pekerja sebuah perusahaan.
Jumlah suku cadang cacat yang diproduksi di suatu pabrik dalam sehari.
Nilai yang diperoleh pada ujian yang dilakukan siswa dalam suatu mata kuliah.
Profitabilitas saham perusahaan yang terdaftar di bursa.

Grafik distribusi normal

Setelah kita melihat apa itu distribusi normal dan beberapa contoh distribusi probabilitas jenis ini, mari kita lihat seperti apa grafiknya untuk lebih memahami konsepnya.

Pada grafik berikut, Anda dapat melihat bagaimana fungsi kepadatan distribusi normal bervariasi tergantung pada nilai rata-rata aritmatika dan deviasi standarnya.

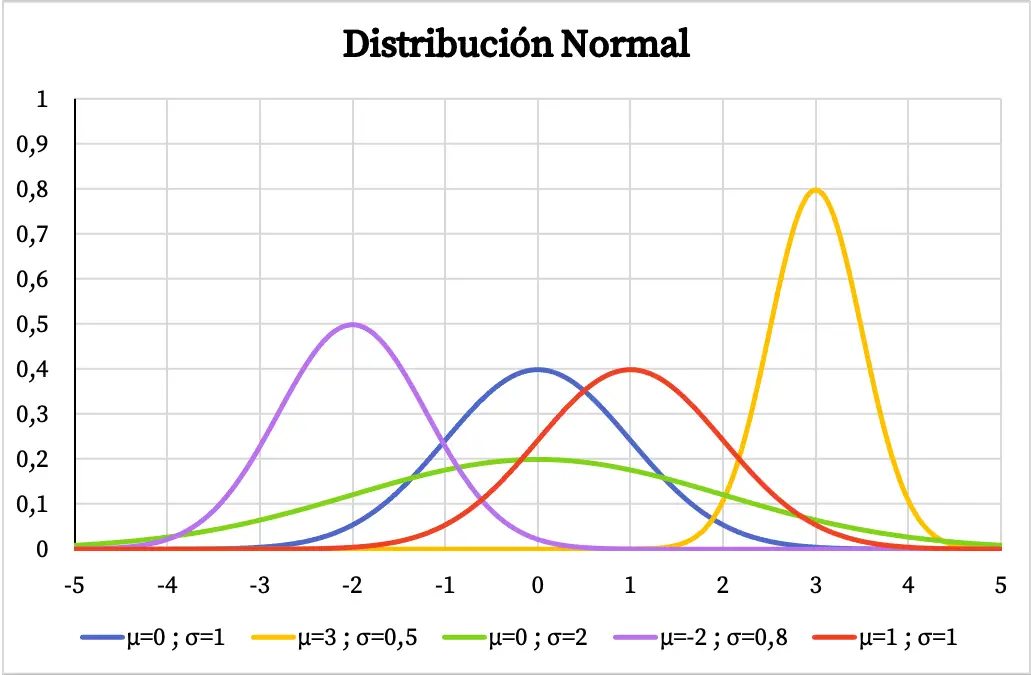
Memiliki bentuk lonceng yang berpusat pada mean aritmatika, jika suatu variabel berdistribusi normal berarti nilai yang paling sering diulang adalah mean dan nilai di sekitar mean lebih sering berulang dibandingkan nilai ekstrim. Demikian pula, semakin besar deviasi standar distribusi normal, semakin datar bentuk representasi grafisnya.

Di sisi lain, grafik fungsi probabilitas kumulatif berdistribusi normal juga bergantung pada nilai mean aritmatika dan deviasi standarnya, seperti terlihat pada gambar berikut:

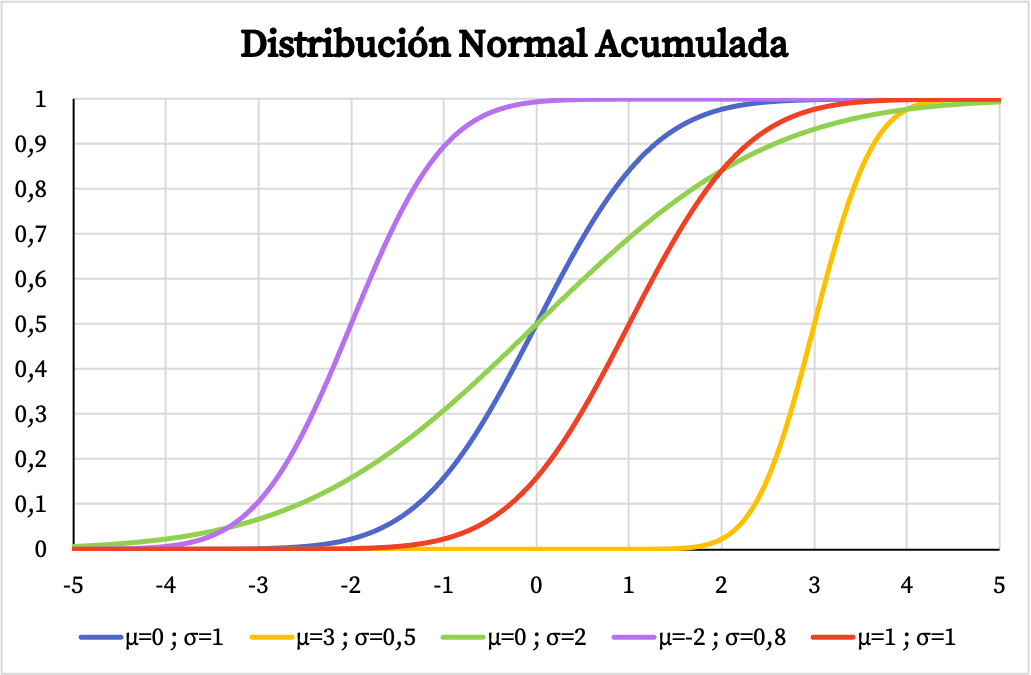
Fungsi kepadatan dan fungsi distribusi dari distribusi normal memungkinkan untuk menghitung probabilitas yang terkait dengan distribusi ini. Namun, daripada menggunakan rumusnya, Anda bisa langsung menggunakan tabel distribusi normal karena lebih cepat. Anda dapat melihat tabel ini di tautan berikut:

➤ Lihat: Tabel distribusi normal

Ciri-ciri berdistribusi normal

Distribusi normal mempunyai ciri-ciri sebagai berikut:

Distribusi normal bergantung pada dua parameter karakteristik, yaitu mean aritmatika (μ) dan deviasi standar (σ).

$X\sim N(\mu,\sigma)$

Distribusi normal dapat bernilai positif dan negatif, sehingga domain distribusi normal terdiri dari bilangan real.

$x\in \mathbb{R}$

Median dan modus distribusi normal sama dengan mean aritmatika distribusi tersebut.

$Me=Mo=\mu$

Koefisien skewness dan koefisien kurtosis berdistribusi normal adalah nol.

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

Rumus fungsi kepadatan berdistribusi normal adalah:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

Demikian pula rumus fungsi probabilitas kumulatif berdistribusi normal adalah:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

Penerapan teorema limit pusat adalah bahwa distribusi Poisson dapat mendekati distribusi normal jika nilai λ cukup besar.

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

Penerapan lain dari teorema limit pusat adalah bahwa distribusi binomial dapat didekati dengan distribusi normal untuk kumpulan data dengan jumlah observasi yang banyak.

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

Distribusi normal standar

Distribusi normal standar , juga disebut distribusi normal satuan , adalah kasus distribusi normal yang paling sederhana. Lebih tepatnya distribusi normal baku adalah distribusi normal dengan nilai mean dan deviasi standar masing-masing sama dengan 0 dan 1.

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Perhatikan bahwa setiap distribusi normal dapat diubah menjadi distribusi normal standar dengan menerapkan proses yang disebut pengetikan, yang melibatkan pengurangan rata-rata aritmatika dari setiap nilai dan kemudian membaginya dengan deviasi standarnya.

Selain itu, distribusi normal standar digunakan untuk menentukan probabilitas distribusi normal menggunakan tabel probabilitasnya. Jadi, untuk mencari probabilitas berdistribusi normal, pertama-tama masukkan variabel untuk mengubahnya menjadi distribusi normal standar dan, kemudian, kita lihat di tabel untuk melihat berapa nilai probabilitas yang sesuai. Untuk mengetahui lebih lanjut, klik tautan berikut:

➤ Lihat: Distribusi Normal Standar

Distribusi normal dan aturan empiris

Dalam statistik, aturan praktis , juga disebut aturan 68-95-99.7 , adalah aturan yang menentukan persentase nilai dalam distribusi normal yang berada dalam tiga standar deviasi mean.

Lebih khusus lagi, aturan praktisnya menyatakan sebagai berikut:

68% nilai dalam distribusi normal terletak dalam satu standar deviasi mean.
95% nilai dalam distribusi normal terletak dalam dua standar deviasi mean.
99,7% nilai dalam distribusi normal berada dalam tiga standar deviasi mean.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya