Distribusi eksponensial

Oleh Benjamin anderson Agustus 3, 2023 Kemungkinan 0 Komentar

Artikel ini menjelaskan apa itu distribusi eksponensial dalam statistik dan kegunaannya. Demikian pula, Anda akan menemukan apa saja sifat-sifat distribusi eksponensial serta rumusnya, grafiknya, dan latihan yang diselesaikan. Selain itu, Anda dapat menghitung probabilitas apa pun dengan kalkulator distribusi eksponensial online.

Apa itu distribusi eksponensial?

Distribusi eksponensial merupakan distribusi probabilitas kontinu yang digunakan untuk memodelkan waktu tunggu terjadinya suatu fenomena acak.

Lebih tepatnya, distribusi eksponensial memungkinkan kita menggambarkan waktu tunggu antara dua peristiwa yang mengikuti distribusi Poisson. Oleh karena itu, distribusi eksponensial berkaitan erat dengan distribusi Poisson.

➤ Lihat: Apa yang dimaksud dengan distribusi Poisson?

Distribusi eksponensial mempunyai parameter karakteristik, diwakili oleh huruf Yunani λ dan menunjukkan berapa kali peristiwa yang diteliti diperkirakan terjadi selama periode waktu tertentu.

$X\sim \text{Exp}(\lambda)$

Demikian pula distribusi eksponensial juga digunakan untuk memodelkan waktu hingga terjadi kegagalan. Oleh karena itu, distribusi eksponensial memiliki beberapa penerapan dalam teori keandalan dan kelangsungan hidup.

Contoh Distribusi Eksponensial

Setelah kita mengetahui pengertian distribusi eksponensial, mari kita lihat beberapa contoh distribusi jenis ini untuk lebih memahami konsepnya.

Contoh distribusi eksponensial:

Waktu yang berlalu antara dua panggilan di pusat panggilan.
Waktu seseorang harus menunggu hingga taksi gratis lewat di jalan tertentu.
Waktu tunggu hingga pelanggan baru memasuki toko.
Waktu yang berlalu antara dua pengguna berbeda yang memasuki halaman web.
Waktu yang berlalu di bandara antara lepas landasnya satu pesawat dan keberangkatan pesawat lainnya.

Rumus distribusi eksponensial

Rumus fungsi kepadatan yang mendefinisikan perhitungan probabilitas distribusi eksponensial adalah sama dengan λ dikalikan angka e pangkat negatif λ dikalikan x.

Dengan kata lain rumus menghitung probabilitas distribusi eksponensial adalah sebagai berikut:

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung peluang suatu variabel yang mengikuti distribusi eksponensial.

Sedangkan rumus untuk menghitung probabilitas kumulatif dari distribusi eksponensial adalah sebagai berikut:

$P[X\leq x]=1-e^{-\lambda x}$

Grafik distribusi eksponensial

Pada bagian ini Anda dapat melihat representasi grafis dari fungsi kepadatan dan fungsi distribusi distribusi eksponensial.

Di bawah ini Anda dapat melihat bagaimana grafik fungsi kepadatan distribusi eksponensial bervariasi tergantung pada nilai parameter λ.

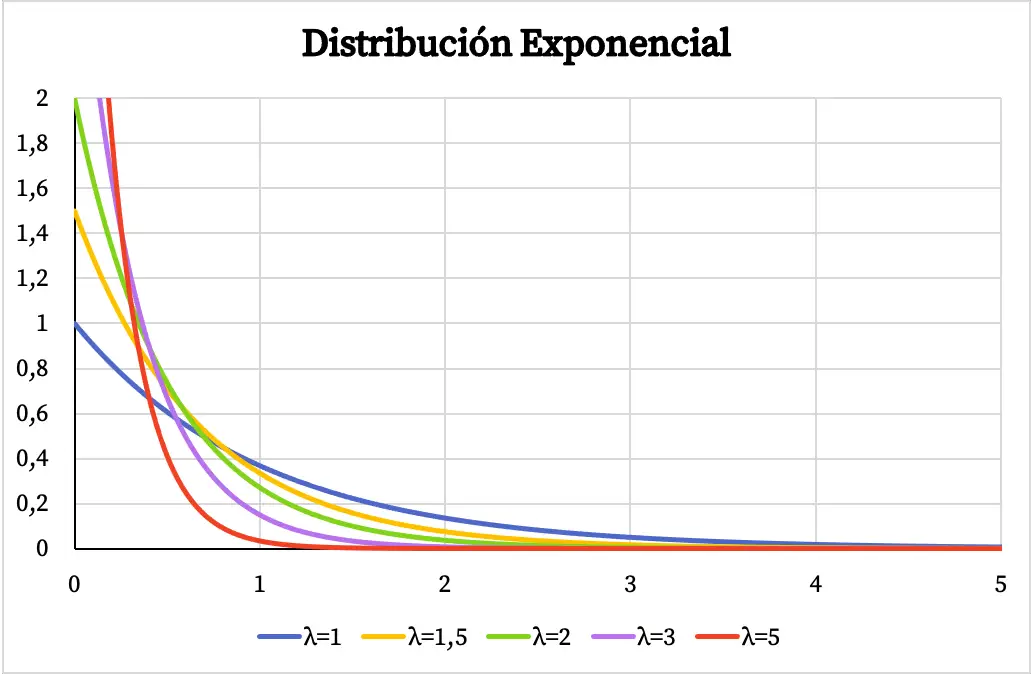
Begitu pula dengan fungsi probabilitas kumulatif dari distribusi eksponensial juga bergantung pada nilai parameter λ, seperti terlihat pada grafik berikut:

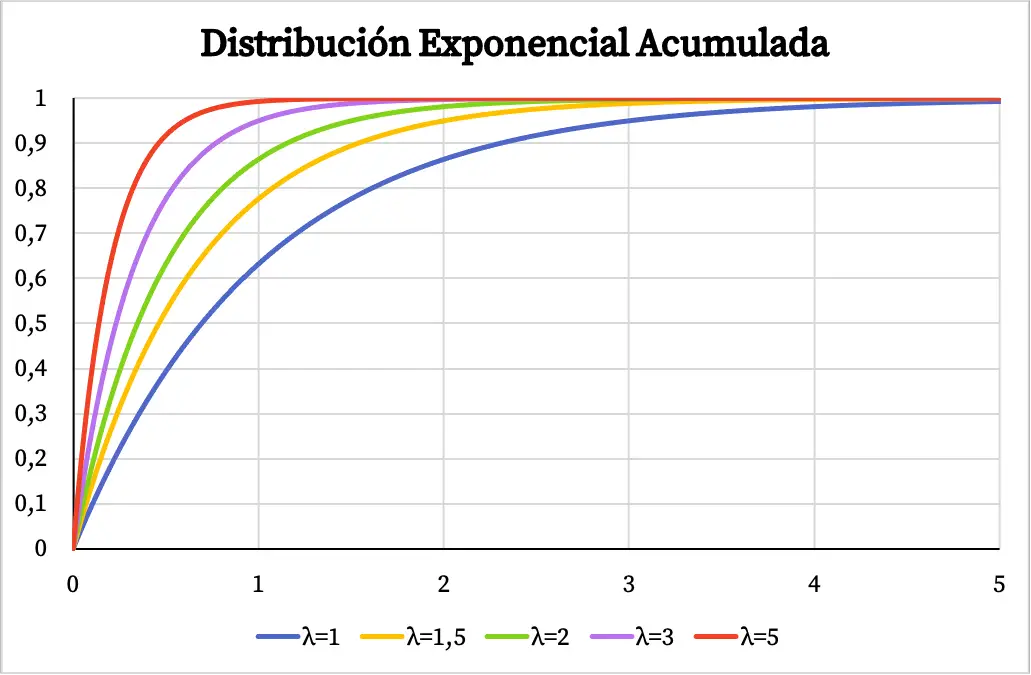
grafik probabilitas distribusi kumulatif eksponensial

Latihan terpecahkan tentang distribusi eksponensial

Rata-rata, λ=1 pengguna/mnt mengakses halaman web tertentu. Berapa peluang terambilnya waktu antara dua pengguna yang masuk adalah 3 menit? Dan peluangnya sama dengan atau kurang dari 2 menit?

Distribusi yang mendefinisikan variabel acak dari masalah ini adalah distribusi eksponensial, karena kita mempelajari waktu yang berlalu dari saat suatu peristiwa terjadi (masuknya pengguna ke halaman web) hingga peristiwa yang sama terjadi lagi.

$X\sim \text{Exp}(1)$

Oleh karena itu, untuk menghitung probabilitas waktu yang berlalu antara masuknya dua pengguna berbeda adalah tiga menit, kita perlu menerapkan rumus fungsi kepadatan (lihat di atas):

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

Sebaliknya, untuk menentukan probabilitas kumulatif, kita harus menggunakan rumus fungsi distribusi dari distribusi eksponensial:

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

Ciri-ciri distribusi eksponensial

Distribusi eksponensial mempunyai ciri-ciri sebagai berikut:

Distribusi eksponensial mempunyai parameter karakteristik, λ, yang menunjukkan berapa kali fenomena yang diteliti diperkirakan akan terjadi selama periode waktu tertentu.

$X\sim \text{Exp}(\lambda)$

Distribusi eksponensial tidak boleh bernilai negatif, sehingga domain distribusi eksponensial terdiri dari semua bilangan real yang lebih besar atau sama dengan nol.

$x\in [0,+\infty)$

Rata-rata distribusi eksponensial sama dengan satu dibagi parameter karakteristik λ.

$E[X]=\cfrac{1}{\lambda}$

Varians dari distribusi eksponensial adalah kuadrat dari meannya, oleh karena itu varians dari distribusi eksponensial setara dengan satu pada koefisien λ kuadrat.

$Var(X)=\cfrac{1}{\lambda^2 }$

Berapa pun nilai λ, koefisien asimetri distribusi eksponensial selalu sama dengan 2.

$A=2$

Demikian pula koefisien kurtosis dari setiap distribusi eksponensial selalu setara dengan 9.

$C=9$

Rumus fungsi kepadatan distribusi eksponensial adalah:

$P[X=x]=\lambda e^{-\lambda x}$

Sedangkan rumus fungsi probabilitas kumulatif berdistribusi eksponensial adalah sebagai berikut:

$P[X\leq x]=1-e^{-\lambda x}$

Distribusi eksponensial adalah salah satu dari sedikit distribusi probabilitas dengan properti kehabisan memori. Sifat ini berarti bahwa terjadinya suatu peristiwa di masa lalu tidak mempengaruhi kemungkinan terjadinya peristiwa tersebut di masa yang akan datang. Misalnya, dalam distribusi eksponensial, kemungkinan pengguna baru akan mengakses halaman web dalam waktu kurang dari satu menit tidak bergantung pada apakah pengguna baru saja masuk atau belum ada pengguna yang masuk sejak saat itu. lebih dari sepuluh menit.

$P[X>x+y|X>y]=P[X>x]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”254″ style=”vertical-align: -5px;”></p> </p> <h2 class=$ Kalkulator Distribusi Eksponensial

Masukkan nilai parameter λ dan nilai x ke dalam kalkulator berikut untuk menghitung probabilitas. Anda perlu memilih probabilitas yang ingin Anda hitung dan memasukkan angka menggunakan titik sebagai pemisah desimal, misalnya 0,50.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya