Cara menerapkan teorema limit pusat di r (dengan contoh)

Teorema limit pusat menyatakan bahwadistribusi sampling dari mean sampel mendekati normal jika ukuran sampel cukup besar, meskipun distribusi populasi tidak normal.

Teorema limit pusat juga menyatakan bahwa distribusi sampling akan mempunyai sifat-sifat sebagai berikut:

1. Rata-rata distribusi sampling akan sama dengan rata-rata distribusi populasi:

x = μ

2. Simpangan baku distribusi sampling akan sama dengan simpangan baku distribusi populasi dibagi jumlah sampel:

s = /n

Contoh berikut menunjukkan bagaimana menerapkan teorema limit pusat di R.

Contoh: penerapan teorema limit pusat pada R

Misalkan lebar cangkang penyu mengikuti distribusi seragam dengan lebar minimal 2 inci dan lebar maksimal 6 inci.

Artinya, jika kita memilih kura-kura secara acak dan mengukur lebar cangkangnya, kemungkinan lebar cangkangnya juga antara 2 dan 6 inci .

Kode berikut menunjukkan cara membuat kumpulan data di R yang berisi pengukuran lebar karapas 1.000 penyu, yang didistribusikan secara merata antara 2 dan 6 inci:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

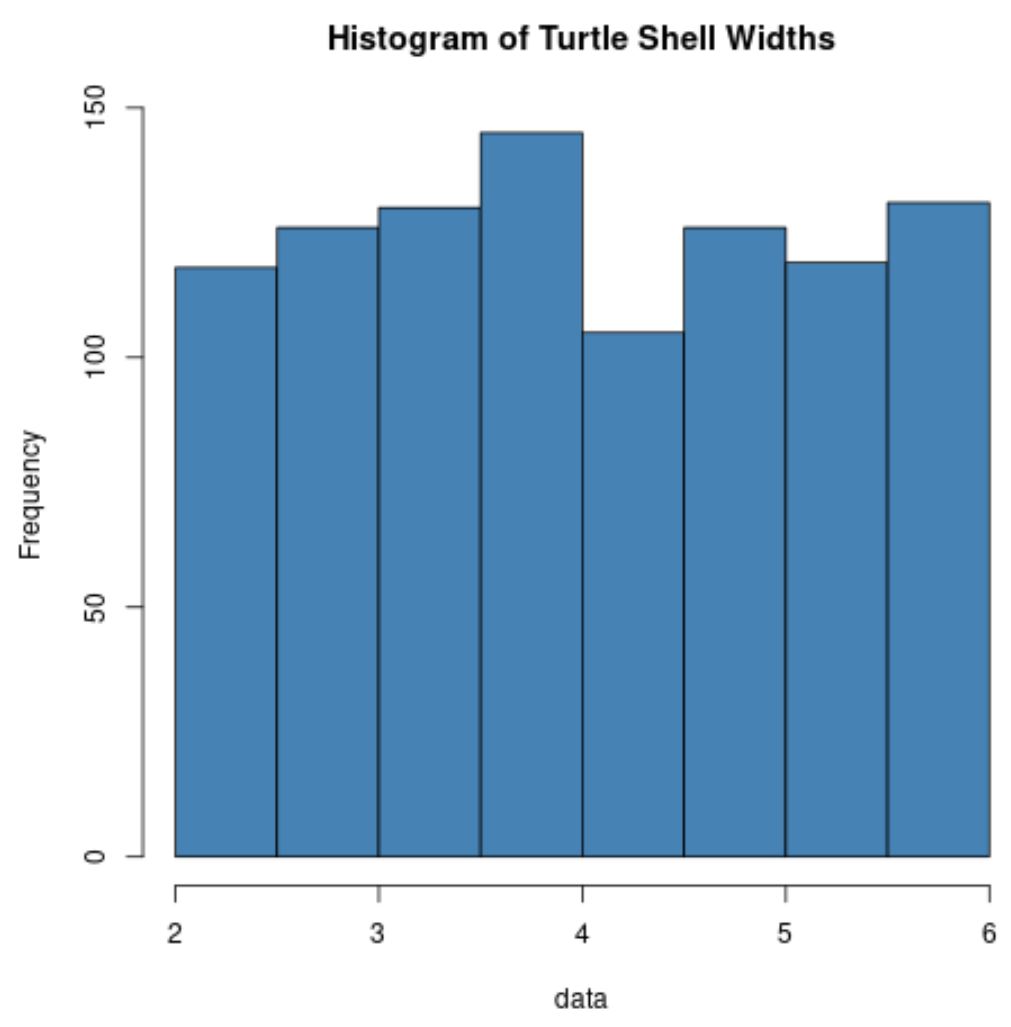
Perlu diketahui bahwa sebaran lebar cangkang penyu biasanya tidak terdistribusi sama sekali.

Sekarang bayangkan kita mengambil sampel acak berulang dari 5 penyu dari populasi ini dan mengukur rata-rata sampel berulang kali.

Kode berikut menunjukkan cara melakukan proses ini di R dan membuat histogram untuk memvisualisasikan distribusi rata-rata sampel:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

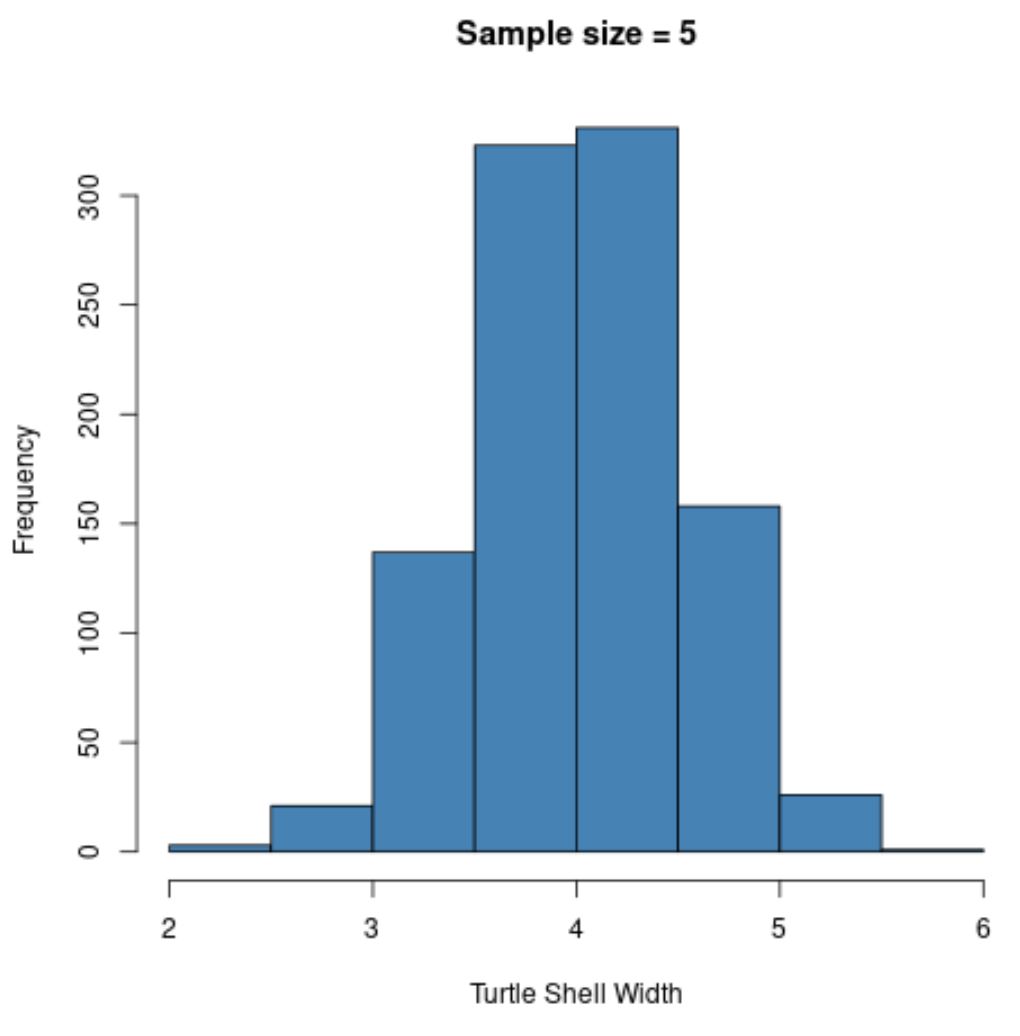
Perhatikan bahwa distribusi sampling dari rata-rata sampel tampak terdistribusi normal, meskipun distribusi asal sampel tidak terdistribusi normal.

Catat juga mean sampel dan deviasi standar sampel untuk distribusi sampling ini:

• x̄ : 4.008
• s : 0,517

Sekarang misalkan kita meningkatkan ukuran sampel yang kita gunakan dari n=5 menjadi n=30 dan membuat ulang histogram dari sampel tersebut:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

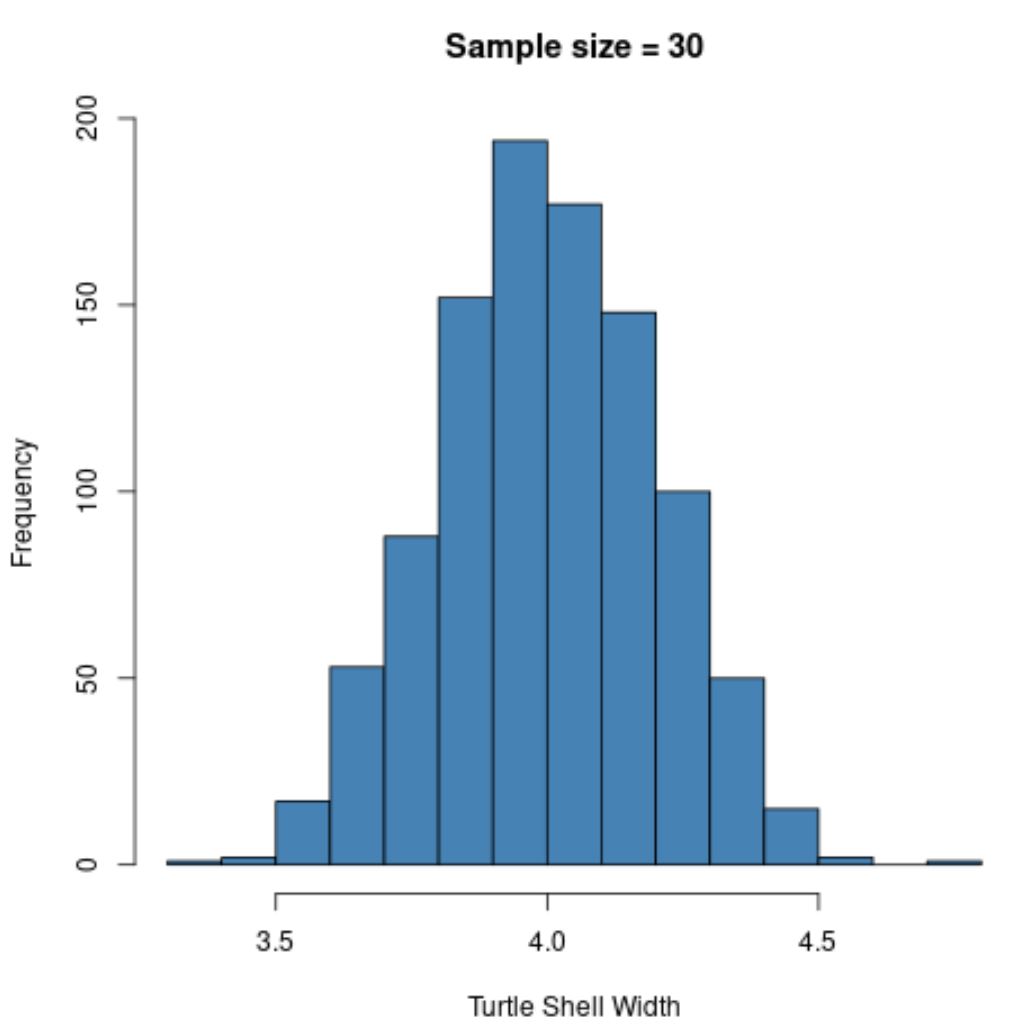
Distribusi pengambilan sampel kembali terdistribusi normal , tetapi simpangan baku sampel lebih kecil lagi:

• s : 0,200

Hal ini karena kita menggunakan ukuran sampel yang lebih besar (n=30) dibandingkan contoh sebelumnya (n=5), sehingga simpangan baku mean sampel menjadi lebih kecil.

Jika kita terus menggunakan sampel yang lebih besar dan lebih besar, kita akan menemukan bahwa deviasi standar sampel menjadi semakin kecil.

Ini menggambarkan teorema limit pusat dalam praktiknya.

Sumber daya tambahan

Sumber daya berikut memberikan informasi tambahan tentang teorema limit pusat:

Pengantar Teorema Limit Pusat
Kalkulator Teorema Batas Pusat
5 Contoh Penggunaan Teorema Limit Pusat dalam Kehidupan Nyata