Cara membuat plot sisa parsial di r
Regresi linier berganda merupakan metode statistik yang dapat kita gunakan untuk memahami hubungan antara beberapa variabel prediktor dan variabel respon .
Namun salah satu asumsi utama regresi linier berganda adalah adanya hubungan linier antara setiap variabel prediktor dan variabel respon.
Jika asumsi ini tidak terpenuhi, maka hasil model regresi mungkin tidak dapat diandalkan.
Salah satu cara untuk menguji asumsi ini adalah dengan membuat plot residu parsial , yang menampilkan residu variabel prediktor relatif terhadap variabel respons.
Contoh berikut menunjukkan cara membuat plot sisa parsial untuk model regresi di R.
Contoh: Cara membuat plot sisa parsial di R
Misalkan kita memasang model regresi dengan tiga variabel prediktor di R:
#make this example reproducible set. seeds (0) #define response variable y <- c(1:1000) #define three predictor variables x1 <- c(1:1000)*runif(n=1000) x2 <- (c(1:1000)*rnorm(n=1000))^2 x3 <- (c(1:1000)*rnorm(n=1000))^3 #fit multiple linear regression model model <- lm(y~x1+x2+x3))
Kita dapat menggunakan fungsi crPlots() dari paket car di R untuk membuat plot sisa parsial untuk setiap variabel prediktor dalam model:
library (car) #create partial residual plots crPlots(model)
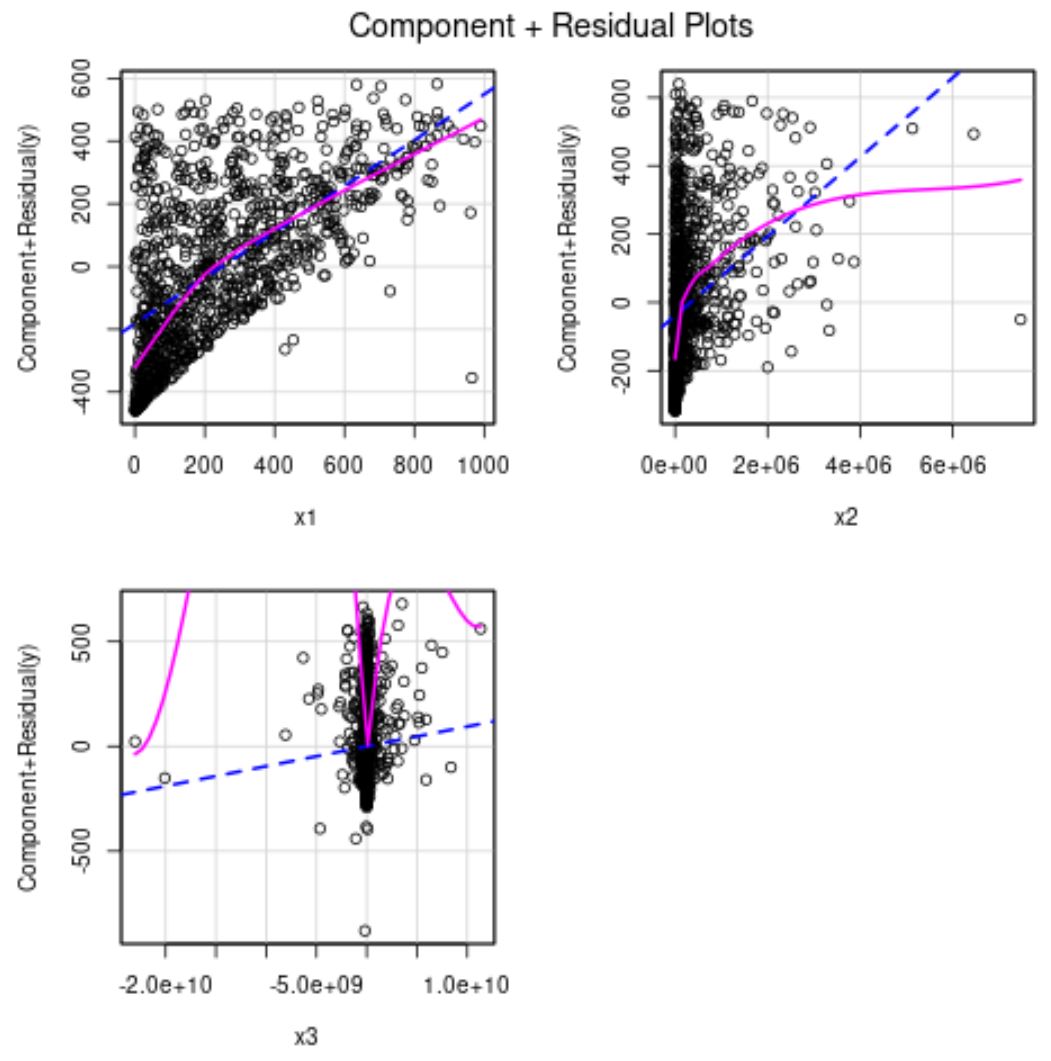
Garis biru menunjukkan residu yang diharapkan jika hubungan antara prediktor dan variabel respon linier. Garis merah muda menunjukkan residu sebenarnya.
Jika kedua garis tersebut berbeda nyata, maka hal ini menunjukkan adanya hubungan nonlinier.
Dari grafik di atas terlihat bahwa residu x2 dan x3 tampak non-linier.
Hal ini melanggar asumsi linearitas regresi linier berganda. Salah satu cara untuk menyelesaikan masalah ini adalah dengan menggunakan transformasi akar kuadrat atau kubik pada variabel prediktor:
library (car) #fit new model with transformed predictor variables model_transformed <- lm(y~x1+sqrt(x2)+log10(x3^(1/3))) #create partial residual plots for new model crPlots(model_transformed)
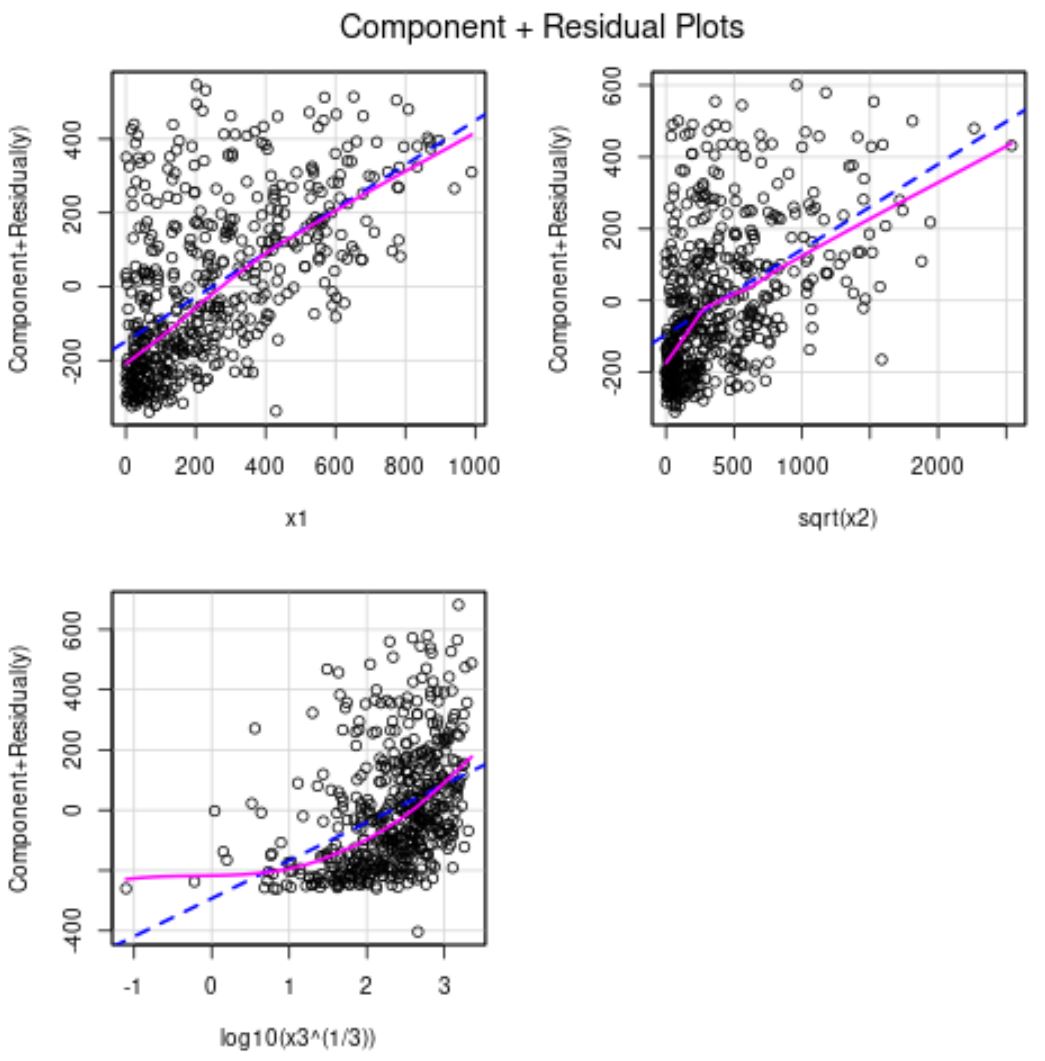
Dari plot sisa parsial terlihat bahwa x2 kini memiliki hubungan yang lebih linier dengan variabel respon.
Variabel prediktor x3 masih agak nonlinier, jadi kami mungkin memutuskan untuk mencoba transformasi lain atau mungkin menghapus variabel tersebut dari model sama sekali.
Sumber daya tambahan
Tutorial berikut menjelaskan cara membuat plot umum lainnya di R:
Cara membuat plot diagnostik di R
Cara membuat plot skala dan lokasi di R
Cara membuat plot sisa di R