Ketiga hipotesis dirumuskan dalam uji t berpasangan
Uji-t sampel berpasangan digunakan untuk membandingkan rata-rata dua sampel ketika setiap observasi pada satu sampel dapat dikaitkan dengan observasi pada sampel lainnya.
Jenis pengujian ini membuat asumsi berikut tentang data:
1. Independensi: setiap observasi harus independen terhadap observasi lainnya.
2. Normalitas: Perbedaan antar pasangan harus terdistribusi secara normal.
3. Tidak ada perbedaan yang ekstrim: Tidak boleh ada perbedaan yang ekstrim.
Jika satu atau lebih asumsi ini tidak terpenuhi, hasil uji-t sampel berpasangan mungkin tidak dapat diandalkan atau menyesatkan.
Pada tutorial ini kami memberikan penjelasan masing-masing asumsi, cara menentukan apakah asumsi tersebut terpenuhi, dan apa yang harus dilakukan jika asumsi tersebut dilanggar.
Hipotesis 1: Kemandirian
Uji-t sampel berpasangan mengasumsikan bahwa setiap observasi tidak bergantung pada semua observasi lainnya.
Bagaimana memverifikasi hipotesis ini
Cara paling sederhana untuk memverifikasi asumsi ini adalah dengan memverifikasi bahwa setiap observasi dikumpulkan dengan menggunakan metode random sampling .
Jika metode pengambilan sampel acak digunakan (seperti pengambilan sampel acak sederhana), maka kita dapat berasumsi bahwa setiap observasi tidak bergantung pada semua observasi lainnya.
Apa yang harus dilakukan jika asumsi ini tidak dipatuhi
Jika asumsi ini tidak terpenuhi, maka hasil uji t sampel berpasangan tidak valid sama sekali.
Dalam skenario ini, yang terbaik adalah mengumpulkan observasi baru menggunakan metode pengambilan sampel acak untuk memastikan bahwa setiap observasi bersifat independen.
Hipotesis 2: normalitas
Uji-t sampel berpasangan mengasumsikan bahwa perbedaan antar pasangan harus berdistribusi normal.
Ini adalah asumsi yang penting karena jika perbedaan antar pasangan tidak terdistribusi secara normal, maka tidak valid menggunakan nilai p dari pengujian untuk menarik kesimpulan.
Bagaimana memverifikasi hipotesis ini
Cara termudah untuk menguji hipotesis ini adalah dengan membuat histogram dari perbedaan berpasangan dan memeriksa secara visual apakah histogram tersebut berbentuk lonceng atau tidak.
Misalnya, jika histogramnya terlihat seperti ini, asumsi normalitasnya terpenuhi:
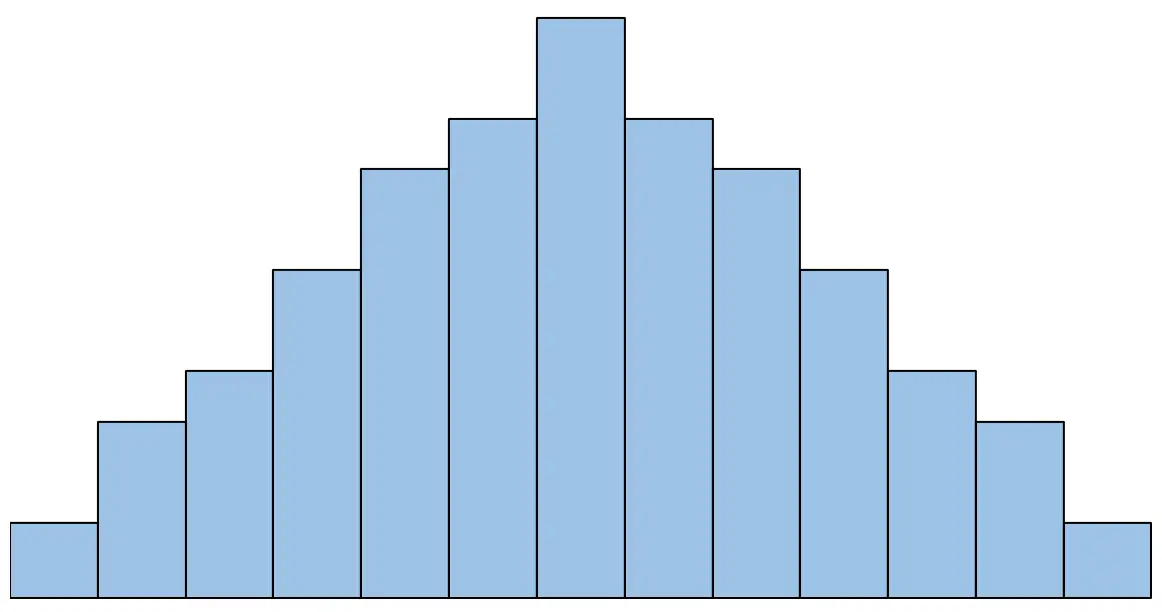
Namun jika histogramnya terlihat seperti ini, asumsi normalitasnya tidak terpenuhi:
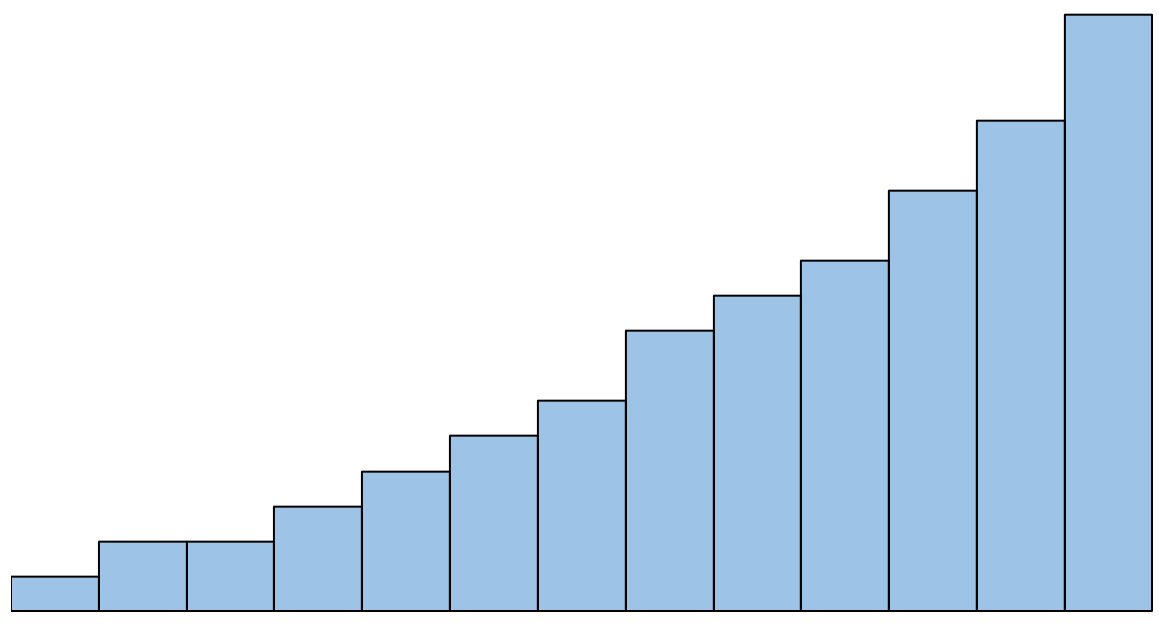
Apa yang harus dilakukan jika asumsi ini tidak dipatuhi
Jika asumsi ini dilanggar, kita dapat melakukan uji peringkat bertanda Wilcoxon , yang dianggap setara nonparametrik dari uji-t sampel berpasangan dan tidak mengasumsikan bahwa perbedaan berpasangan terdistribusi secara normal.
Hipotesis 3: tidak ada outlier yang ekstrim
Uji-t sampel berpasangan mengasumsikan bahwa tidak ada outlier ekstrim dalam data.
Bagaimana memverifikasi hipotesis ini
Cara termudah untuk menguji hipotesis ini adalah dengan membuat plot kotak dari perbedaan berpasangan dan memeriksa secara visual apakah ada outlier.
Misalnya, plot kotak perbedaan berpasangan terlihat seperti ini:
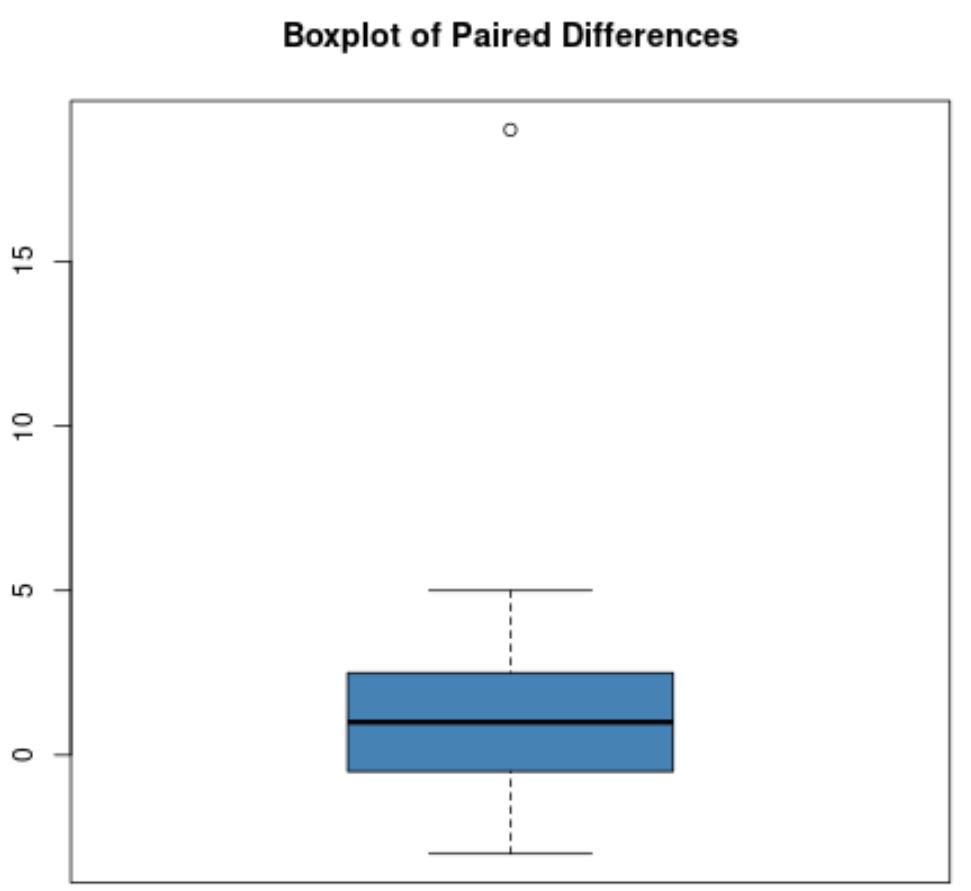
Sebagian besar perbedaan berpasangan mendekati nol, namun ada satu perbedaan berpasangan yang sama dengan sekitar 19, yang jelas merupakan outlier.
Catatan : Lingkaran biasanya digunakan dalam plot kotak untuk menunjukkan outlier.
Namun, misalkan plot kotak perbedaan berpasangan terlihat seperti ini:
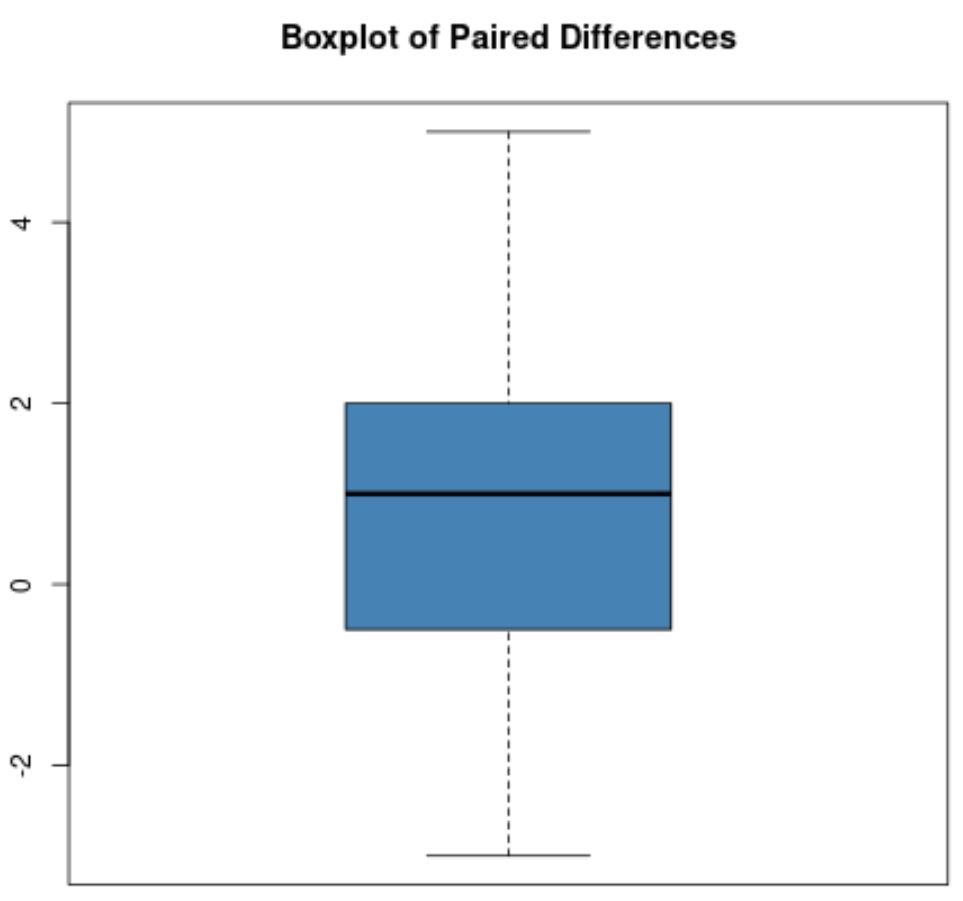
Tidak ada outlier yang jelas pada diagram kotak ini, jadi kita asumsikan tidak ada outlier yang ekstrim pada data.
Apa yang harus dilakukan jika asumsi ini tidak dipatuhi
Jika asumsi ini dilanggar, hasil uji-t sampel berpasangan dapat dipengaruhi oleh outlier secara tidak normal.
Dalam skenario ini, Anda dapat menghapus outlier jika Anda yakin outlier tersebut mewakili titik data yang salah atau merupakan akibat dari kesalahan entri data.
Alternatifnya, Anda dapat menyimpan outlier dan mencatatnya saat melaporkan hasil uji-t sampel berpasangan.
Sumber daya tambahan
Tutorial berikut menjelaskan asumsi yang dibuat dalam uji statistik lainnya:
Keempat hipotesis dirumuskan dalam uji t
Empat hipotesis uji chi-kuadrat
Empat hipotesis uji parametrik